Fractals
Hidden Beauty Revealed in Mathematics
Did you know that amazing, beautiful shapes have been built into numbers? Believe it or not, numbers like 1, 2, 3, etc., contain a “secret code”—a hidden beauty embedded within them.
Did you know that amazing, beautiful shapes have been built into numbers? Believe it or not, numbers like 1, 2, 3, etc., contain a “secret code”—a hidden beauty embedded within them. Numbers have existed from the beginning of creation, yet researchers have only recently discovered the hidden shapes that the Lord placed within them.1 Such beauty defies a secular explanation but confirms biblical creation.
The strange shape in Figure 1 is a sort of “map.” Most maps that we think of are representations of something physical, like a roadmap or a map of a country. But the map in Figure 1 does not represent a physical object; instead it represents a set of numbers. In mathematics, the term “set” refers to a group of numbers that have a common property. For example, there is the set of positive numbers (4 and 7 belong to this set; -3 and 0 do not).
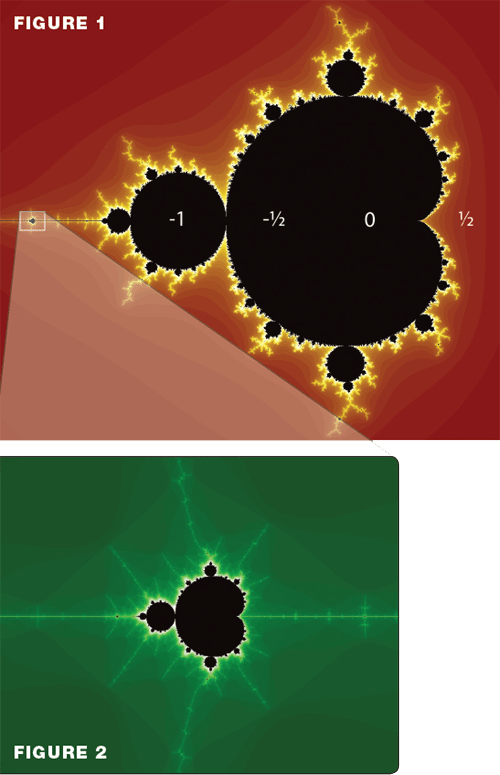
A few decades ago, researchers discovered a very strange and interesting set called “the Mandelbrot set.”2 Figure 1 is a map (a plot) that shows which numbers belong to the Mandelbrot set.
What do these images mean?
A “set” is a group of numbers that all have a common property. For example, the numbers 4 and 6 are part of the set of even numbers, whereas 3 and 7 do not belong to that set. The Mandelbrot set is a group of numbers defined by a simple formula which is explained in the In-Depth box in this article. Some numbers belong to the Mandelbrot set, and others don’t.
Figure 1 is a plot—a graph that shows which numbers are part of the Mandelbrot set. Points that are black represent numbers that are part of the set. So, the numbers, -1, -1/2, and 0 are part of the Mandelbrot set. Points that are colored (red and yellow) are numbers that do not belong to the Mandelbrot set, such as the number 1/2. Although the formula that defines the Mandelbrot set is extremely simple, the plotted shape is extremely complex and interesting. When we zoom in on this shape, we see that it contains beautiful spirals and streamers of infinite complexity. Such complexity has been built into numbers by the Lord.
The Mandelbrot set (Figure 1) is infinitely detailed. In Figure 2, we have zoomed in on the “tail” of the Mandelbrot set. And what should we find but another (smaller) version of the original. This new, smaller Mandelbrot set also has a tail containing a miniature version of itself, which has a miniature version of itself, etc.—all the way to infinity.
The way to find if a number belongs to the Mandelbrot set is to put it through a particular formula (the details are shown in the In-Depth box in this article). In this way, we can check every possible number to see if it belongs to the Mandelbrot set, and then plot the results on a graph. We color the point black if it does belong to the Mandelbrot set; we give it a different color if it does not. For example, in Figure 1 we can see that the numbers 0 and -1 are part of the Mandelbrot set, whereas the number 1/2 is not.
Evolution cannot account for fractals. These shapes have existed since creation and cannot have evolved since numbers cannot be changed.
The Mandelbrot set is a very complex and detailed shape; in fact it is infinitely detailed. If we zoom in on a graphed piece of the Mandelbrot set, we see that it appears even more complicated than the original. In Figure 2, we have zoomed in on the “tail” of the Mandelbrot set. And what should we find but another (smaller) version of the original; a “baby” Mandelbrot set is built into the tail of the “parent.” This new, smaller Mandelbrot set also has a tail containing a miniature version of itself, which has a miniature version of itself, etc.—all the way to infinity. The Mandelbrot set is called a “fractal”3 since it has an infinite number of its own shape built into itself.
In Figure 3, we have zoomed into a region called the “Valley of Seahorses.” By zooming in on one of these “seahorses” we can see that it is a very complex spiral (see Figure 4). If we continue to zoom in, the order and beauty continue to increase as shown in Figures 5 and 6. As we zoom in yet again, we see in Figure 7 another “baby” version of the original Mandelbrot set at the center of the intersecting spirals; it appears virtually the same as the original shape, but it is 5 million times smaller.
Where did this incredible organization and beauty come from? Some might say that a computer produced this organization and beauty. After all, a computer was used to produce the graphs in the figures. But the computer did not create the fractal. It only produced the map—the representation of the fractal. A graph of something is not the thing itself, just as a map of the United States is not the same thing as the United States. The computer was merely a tool that was used to discover a shape that is an artifact of the mathematics itself.4
God alone can take credit for mathematical truths, such as fractals. Such transcendent truths are a reflection of God’s thoughts. Therefore when we discover mathematical truths we are, in the words of the astronomer Johannes Kepler, “thinking God’s thoughts after Him.” The shapes shown in the figures have been built into mathematics by the Creator of mathematics. We could have chosen different color schemes for the graphs, but we cannot alter the shape—it is set by God and His nature.
Evolution cannot account for fractals. These shapes have existed since creation and cannot have evolved, since numbers cannot change—the number 7 will never be anything but 7. But fractals are perfectly consistent with biblical creation. The Christian understands that there are transcendent truths because the Bible states many of them.5 A biblical creationist expects to find beauty and order in the universe, not only in the physical universe,6 but in the abstract realm of mathematics as well. This order and beauty is possible because there is a logical God who has imparted order and beauty into His universe.
Infinite Complexity?
This sequence of images (Figures 3–7) shows what happens as we continually zoom in on a very small region of the Mandelbrot set. We start by zooming in on the highlighted region of the Mandelbrot set called the “Valley of Seahorses” (Figure 3). By zooming in on one of these “seahorses” we can see that it is a very complex spiral (Figure 4). We continue to zoom in (the region is indicated by the grayscale inset) in Figures 5, 6 and 7. Figure 7 shows a “baby” Mandelbrot set; it is virtually identical to the original shape, but it is 5 million times smaller.

Figure 3 (click to enlarge)

Figure 4 (click to enlarge)

Figure 5 (click to enlarge)

Figure 6 (click to enlarge)

Figure 7 (click to enlarge)
In-Depth
The formula for the Mandelbrot set is zn+1 = zn2 + c. In this formula, c is the number being evaluated, and z is a sequence of numbers (z0, z1, z2, z3…) generated by the formula. The first number z0 is set to zero; the other numbers will depend on the value of c. If the sequence of zn stays small (zn ≤ 2 for all n), c is then classified as being part of the Mandelbrot set. For example, let’s evaluate the point c = 1. Then the sequence of zn is 0, 1, 2, 5, 26, 677… . Clearly this sequence is not staying small, so the number 1 is not part of the Mandelbrot set. The different shades/colors in the figures indicate how quickly the z sequence grows when c is not a part of the Mandelbrot set.
The complex numbers are also evaluated. Complex numbers contain a “real” part and an “imaginary” part. The real part is either positive or negative (or zero), and the imaginary part is the square-root of a negative number. By convention, the real part of the complex number (RE[c]) is the x-coordinate of the point, and the imaginary part (IM[c]) is the y-coordinate. So, every complex number is represented as a point on a plane. Many other formulae could be substituted and would reveal similar shapes.
Answers Magazine
January – March 2007
This issue discusses topics such as gender equality, abortion, the origin of oil, racism, mand more.
Browse IssueFootnotes
- We don’t normally think of God creating numbers because they are abstract, not physical. But of course, all things were made by God (John 1:3), even the abstract things.
- Named after its discoverer Benoit Mandelbrot.
- The term “fractal” was coined by Benoit Mandelbrot in the 1970s. A fractal contains an infinite number of copies of itself. In some fractals, the copies are exactly the same as the original. However, in other cases (such as the Mandelbrot set), they are slightly different.
- It could be said that we selected the formula that generates the Mandelbrot set. Although this formula defines the set, it did not create it or its complexity. The Mandelbrot set existed long before humans discovered it. Moreover, many other formulae also reveal this complexity and beauty of numbers. So, the principle does not hinge on the exact formula. The complexity and beauty are built into mathematics itself.
- Such as laws of morality.
- The physical universe also contains “fractals” such as snow-flakes. This is not surprising since nature is built on mathematical principles. As such, physical reality mimics the nonphysical world of mathematics. However, unlike pure mathematical fractals, physical fractals (like crystals, clouds, etc.) do not repeat forever since they are comprised of atoms.

Answers in Genesis is an apologetics ministry, dedicated to helping Christians defend their faith and proclaim the good news of Jesus Christ.
- Customer Service 800.778.3390
- Available Monday–Friday | 9 AM–5 PM ET
- © 2026 Answers in Genesis