Carbon-14 Dating

The most well-known of all the radiometric dating methods is radiocarbon dating. Although many people think radiocarbon dating is used to date rocks, it is limited to dating things that contain the element carbon and were once alive (like fossils).

How Radiocarbon Forms

Unlike radiocarbon (¹⁴C), the other radioactive elements used to date rocks—uranium (²³⁸U), potassium (⁴⁰K), and rubidium (⁸⁷Rb)—are not being formed on earth, as far as we know. Thus it appears that God probably created those elements when He made the original earth.

In contrast, radiocarbon forms continually today in the earth’s upper atmosphere. And as far as we know, it has been forming in the earth’s upper atmosphere since the atmosphere was made back on Day Two of Creation Week (part of the expanse, or firmament, described in Genesis 1:6–8).

So how does radiocarbon form? Cosmic rays from outer space are continually bombarding the upper atmosphere of the earth, producing fast-moving neutrons (subatomic particles carrying no electric charge) (Figure 1a).1 These fast-moving neutrons collide with atoms of nitrogen-14, the most abundant element in the upper atmosphere, converting them into radiocarbon (carbon-14) atoms.

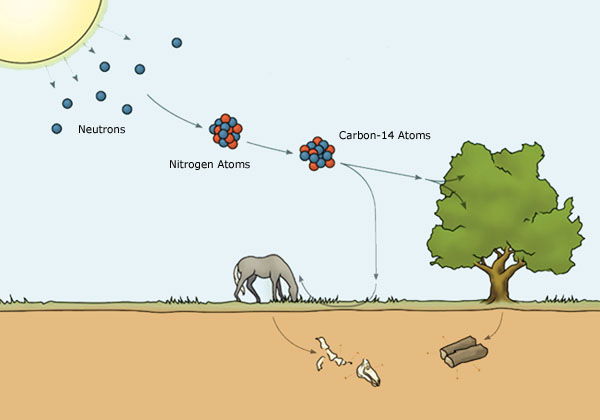
CARBON-14 IS CREATED (Figure 1a): When cosmic rays bombard the earth’s atmosphere, they produce neutrons. These excited neutrons then collide with nitrogen atoms in the atmosphere, changing them into radioactive carbon-14 atoms.

CARBON-14 IS ABSORBED (Figure 1b): Plants absorb this carbon-14 during photosynthesis. When animals eat the plants, the carbon-14 enters their bodies. The carbon-14 in their bodies breaks down to nitrogen-14 and escapes at the same rate as new carbon-14 is added. So the level of carbon-14 remains stable.

CARBON-14 IS DEPLETED (Figure 1c): When an animal dies the carbon-14 continues to break down to nitrogen-14 and escapes, while no new carbon-14 is added. By comparing the surviving amount of carbon-14 to the original amount, scientists can calculate how long ago the animal died.

Since the atmosphere is composed of about 78% nitrogen,2 a lot of radiocarbon atoms are produced—in total about 16.5 pounds (7.5 kg) per year. These rapidly combine with oxygen atoms (the second most abundant element in the atmosphere, at 21%) to form carbon dioxide (CO₂).

This carbon dioxide, now radioactive with carbon-14, is otherwise chemically indistinguishable from the normal carbon dioxide in the atmosphere, which is slightly lighter because it contains normal carbon-12. Radioactive and non-radioactive carbon dioxide mix throughout the atmosphere, and dissolve into the oceans.

Through photosynthesis carbon dioxide enters plants and algae, bringing radiocarbon into the food chain. Radiocarbon then enters animals as they consume the plants (Figure 1b). So even we humans are radioactive because of trace amounts of radiocarbon in our bodies.

Determining the Rate of Radiocarbon Decay

After radiocarbon forms, the nuclei of the carbon-14 atoms are unstable, so over time they progressively decay back to nuclei of stable nitrogen-14.3 A neutron breaks down to a proton and an electron, and the electron is ejected. This process is called beta decay. The ejected electrons are called beta particles and make up what is called beta radiation.

Because it breaks down quickly, carbon-14 is useful for dating creatures that died in the past few thousand years, not millions of years ago.

Not all radiocarbon atoms decay at the same time. Different carbon-14 atoms revert to nitrogen-14 at different times, which explains why radiocarbon decay is considered a random process.

To measure the rate of decay, a suitable detector records the number of beta particles ejected from a measured quantity of carbon over a period of time, say a month (for illustration purposes). Since each beta particle represents one decayed carbon-14 atom, we know how many carbon-14 atoms decay during a month.

Chemists have already determined how many atoms are in a given mass of each element, such as carbon.4 So if we weigh a lump of carbon, we can calculate how many carbon atoms are in it.

If we know what fraction of the carbon atoms are radioactive, we can also calculate how many radiocarbon atoms are in the lump. Knowing the number of atoms that decayed in our sample over a month, we can calculate the radiocarbon decay rate.

The standard way of expressing the decay rate is called the half-life.5 It’s defined as the time it takes half a given quantity of a radioactive element to decay. So if we started with 2 million atoms of carbon-14 in our measured quantity of carbon, then the half-life of radiocarbon would be the time it takes for half, or 1 million, of those atoms to decay. The radiocarbon half-life or decay rate has been determined at 5,730 years.

Using Radiocarbon for Dating

Next comes the question of how scientists use this knowledge to date things. If carbon-14 has formed at a constant rate for a very long time and continually mixed into the biosphere, then the level of carbon-14 in the atmosphere should remain constant.

If the level is constant, living plants and animals should also maintain a constant carbon-14 level in them. The reason is that, as long as the organism is alive, it replaces any carbon molecule that has decayed into nitrogen.

After plants and animals perish, however, they no longer replace molecules damaged by radiocarbon decay. Instead, the radiocarbon atoms in their bodies slowly decay away, so the ratio of carbon-14 atoms to regular carbon atoms will steadily decrease over time (Figure 1c).

Let’s suppose we find a mammoth’s skull and we want to date it to determine how long ago it lived. We can measure in the laboratory how many carbon-14 atoms are still in the skull. If we assume that the mammoth originally had the same number of carbon- 14 atoms in its bones as living animals do today (estimated at one carbon-14 atom for every trillion carbon-12 atoms), then, because we also know the radiocarbon decay rate, we can calculate how long ago the mammoth died. It’s really quite simple.

This dating method is similar to the principle behind an hourglass.6 The sand grains that originally filled the top bowl represent the carbon-14 atoms in the living mammoth just before it died. It’s assumed to be the same number of carbon-14 atoms as in elephants living today. With time those sand grains fall to the bottom bowl, so the new number represents the carbon-14 atoms left in the mammoth skull when we found it.

The difference in the number of sand grains represents the number of carbon-14 atoms that have decayed back to nitrogen-14 since the mammoth died. Because we have measured the rate at which the sand grains fall (the radiocarbon decay rate), we can then calculate how long it took those carbon-14 atoms to decay, which is how long ago the mammoth died.

That’s how the radiocarbon method works. And because the half-life of carbon-14 is just 5,730 years, radiocarbon dating of materials containing carbon yields dates of only thousands of years, not the dates over millions of years that conflict with the framework of earth history provided by the Bible, God’s eyewitness account of history.