Research conducted by Answers in Genesis staff scientists or sponsored by Answers in Genesis is funded solely by supporters’ donations.
Abstract
We here explore a way in which light from distant galaxies can reach earth within the biblical timescale. Though the universe is created mature, we will find that this by itself appears to be insufficient to explain our ability to see distant events, prompting the need for a solution to the “distant starlight problem.” The concept of synchrony conventions in physics is examined. The fact that relativistic physics precludes an absolute, invariant synchrony space is reviewed. We then explore the consequences and motivation for the use of the standard Einstein synchrony convention, followed by an investigation of alternative synchrony conventions. In particular, we find that an observer-centric anisotropic synchrony convention eliminates the distant starlight problem by reducing radially inward-directed light travel-time in the reference frame of the observer to zero. Such a convention implies that everything in the universe has an age of a few thousand years as we currently see it. The biblical basis for such a convention is explored. Potential objections to this synchrony convention are considered. When the anisotropic synchrony convention is applied to standard cosmological parameters, a new young-universe cosmological model emerges which makes falsifiable predictions.
Introduction
According to the Bible, everything in the universe was made in the span of six days (Exodus 20:11); these are clearly ordinary earth rotation days comprised of one evening and one morning (Genesis 1:5). Moreover, this creation happened a few thousand (roughly 6,000) years ago, as deduced from the genealogies we read in sections of the Bible such as Genesis 5 and 11. The clear biblical teaching therefore is that everything in the universe is a few thousand years old. Since light travels a distance of one light year (about 6 trillion miles or 9 trillion kilometers) in one year, it would seem that we should only be able to see objects within a radius of 6,000 light years.1 Objects beyond that distance should not be visible, since presumably their light has not yet reached us. Yet, paradoxically, we can see galaxies whose distances have been measured to be many billions of light years away. This apparent mystery has been often addressed in creation literature as “the distant starlight problem.”
Critics of biblical creation have often attempted to use distant starlight as evidence in favor of the big bang and against Genesis. But such criticisms are logically unsound since the big bang has an ontologically equivalent problem—the horizon problem. Solutions to the horizon problem have been proposed of course, but there is not universal agreement (Lisle 2006). The fact that the universe is very big and also young (by secular standards) is therefore not logically useful as a criticism against the Bible when the favored alternative also has a light travel-time problem.
Mature Creation
It has been suggested that God supernaturally created the beams of light themselves. That is, the light beam from every star to earth is created “in transit” at the same time the stars are created. This light en-route model is often presented in the context of mature creation: the idea that God created the universe fully functional from the start, and that the universe required no time or process to become what God wanted it to be.
Mature creation is sometimes inappropriately referred to as “appearance of age”; however the latter term fallaciously implies that age can be seen or otherwise empirically measured. But since age is not a physical property or substance, it cannot be directly observed. Of course there is a sense in which we say that something appears old or young—a person who looks “young” for his age, or a car that looks quite “old.” In these cases, we are speaking idiomatically, comparing observable characteristics and then making an inference based on comparisons with other samples whose age is known. This of course is not possible with the universe, since there is only one known member of its class (Chaffey and Lisle 2008).
Strictly speaking, something cannot appear old or young, because age is not an observational property. Age is a concept indicative of history, which cannot be observed in the present. When someone says he believes the universe “looks old,” this simply reveals something about the initial conditions he has assumed—not about the universe. Thus, the universe was not created with “appearance of age,” but it was created mature—in the sense that it functioned immediately upon God’s creating it. Just as Adam was created mature, needing no time or process to reach adulthood, so was the universe.
Many arguments against a young universe are indeed easily refuted by pointing out that the universe was made mature, and hence the advocate of an “old earth” has assumed the incorrect initial conditions. Today, for example, trees need a certain amount of time to reach a certain size. But the first trees were created supernaturally, and needed less than a day to reach their size. If someone were to assume that the first trees came about by today’s natural processes (growing from a seed at today’s rate), he or she would vastly overestimate the age.
The overwhelming majority of old-earth, or old-universe arguments are fallacious because they are based on faulty, unbiblical initial conditions. For example, by assuming that the universe began with no size, or that the solar system formed from a nebula, and then extrapolating how long it would take to reach its present state, of course one is bound to reach a faulty age estimate that is inflated by a factor of millions. Old-universe supporters frequently make such mistakes. They have arbitrarily assumed unbiblical initial conditions, and then use the resulting inflated age estimate to argue that the Bible is wrong. But, of course, this simply begs the question.
The Light-in-Transit Model
Mature creation is a biblical concept, and easily shows the majority of old-earth claims to be fallacious. But does distant starlight fall in this category? One of the assumptions involved when light travel times are computed is that the light did indeed originate at the star. If God created the beams of light en-route, then they did not originate at the stars. This would indeed eliminate the distant starlight problem. However, this proposal introduces biblical and philosophical difficulties of its own. I suggest that it is reasonable (and in fact necessary) to suppose that distant starlight did in fact originate from the star, and was not created in transit. There are several reasons to reject the light-in-transit view.
First, there is a serious biblical difficulty with this view. Genesis 1:14–15 indicates that God made the lights in the sky to mark the passage of time and to give light upon the earth. Verse 16 tells us specifically what these lights are: God created the sun, the moon, and the stars also. Verse 17 reiterates that one of the purposes of these light-bearers is to give light upon the earth. The phrase at the end of verse 15 “and it was so” indicates that these light-bearers immediately began to fulfill their God-given purpose—to give light upon the earth.
But this is the problem: if God created the light in-transit, then the light does not really come from the stars. In fact, it could not rightly be called “starlight” at all but rather “Godlight.” If the light en-route model were true, then all stars beyond about 6,000 light years are not yet fulfilling their God-ordained purpose to give light upon the earth, but Genesis 1:14–15 suggests that the stars fulfilled their purpose right from the day of their creation.
There is a serious philosophical difficulty as well concerning the preconditions of intelligibility. These are the things necessary to make knowledge of the universe possible. For example, the basic reliability of our senses is a precondition of intelligibility. Clearly, if our eyes, ears, and other senses did not accurately inform our mind about the outside world, we would have no hope of understanding anything about the universe. We all presume that our senses are basically reliable, that we are not just a brain in a jar being fed electrical impulses about a fictional “Matrix” world.
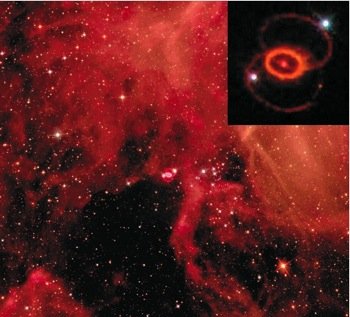
Fig. 1. Supernova 1987A. If the light-in-transit model is correct, then this star never actually existed, and this explosion never really happened. It would mean that this image does not correspond to any real object, but is simply a picture created by God in beams of light.
The preconditions of intelligibility must be true, because without them we could not know anything at all. Therefore, anything that undermines a precondition of intelligibility must be false. But the light-in-transit model undermines the basic reliability of our senses. Consider: the light-in-transit model would mean that all events (supernovae for example—fig. 1) beyond about 6,000 light years have never happened. They would merely be a sequence of images in a beam of light created by God. These images would not correspond to any real event.
But if God is willing to make movies of fictional events at distances beyond 6,000 light years, then why would we arbitrarily assume that He would not also make fictional movies nearby? (Is the tree outside my window real, or is it merely a picture embedded in light beams created by God?) The light-en-route model requires that events we observe beyond about 6,000 light years (which covers the overwhelming majority of the universe) are fictional, and thus our senses are not reliable for those distances. If we cannot believe our eyes for 99.9999% of the universe, then why should we trust them for the other 0.0001% that is nearby? So, light-en-route models lead to the inescapable conclusion that our senses are not generally reliable, in which case it doesn’t make sense to even attempt to understand the universe. Yes, God made the universe mature. But, no, this does not by itself alleviate the distant starlight problem.
Scripture Implies a Synchrony Convention
Genesis itself may suggest a simple answer to distant starlight. In Genesis 1:14–18 God tells us that the stars were created on the fourth day to give light upon the earth. This text also seems to strongly suggest that the stars fulfilled their purpose immediately (“and it was so”). Therefore, it would seem that the light emitted by the stars reached earth instantaneously, or nearly so. This suggests a synchrony convention: a procedure for synchronizing clocks separated by a distance.2
Two events are said to be “simultaneous” if they both happen at the same time. When two events are separated by some distance and we wish to know whether they are simultaneous, we must first establish a system of measuring time at various locations. In particular, we must make certain that any clocks we are using to measure time at the two locations are synchronized. Thus, we must develop a procedure for synchronizing clocks separated by a distance. This turns out to be far more complicated than people might assume at first. Yet, we will find that the correct synchrony convention eliminates the distant starlight problem. Starlight from the most distant galaxy can reach earth on the fourth day of the Creation Week when the correct relativistic synchrony convention is employed.
Simultaneity in the Classical Limit
Before we address relativistic synchrony conventions, it is useful to examine the concept of synchronization in the classical, Newtonian limit. Before the discovery of Special Relativity, measurements of distances and durations were considered to be invariant: absolute and objectively independent of the reference frame (velocity) or position of the observer. Since motion does not affect the passage of time under Newtonian physics, the synchronization of two clocks is trivial. Simply synchronize the two clocks at the same location, and then move them to the desired positions. The clocks remain synchronized in the classical limit. If we imagine doing this process for an infinite number of clocks, and then distributing these clocks in a three-dimensional grid throughout the universe, we could determine the time of any possible event. The clock at the location of the event records the time.
Suppose we want to know if two events in the universe, say two lightning strikes, have happened at the same time. That is, we wish to know if the two events are simultaneous. This is easily accomplished in our system. Simply read the time of the clock at event A at the instant it happens, and compare it with the time of the clock at event B at the moment it happens. If the times are the same, then the two events are said to be simultaneous. If the two events are not simultaneous, then a particle emitted from the first event at just the right velocity could arrive at the location of the second event exactly at the time the second event occurs.
If the two events are close in space, but widely separated in time (the second event happens long after the first), then a slow-moving particle can pass from the first to the second. If the two events are widely separated in space, but only a short amount of time separates them, then a high-speed particle can pass from the first to the second. However, if the two events are simultaneous, no (finite) speed will be fast enough for a particle from one to reach the other. No amount of energy could accelerate the particle (of finite mass) to the infinite speed required to make its trip instantaneous. This leads us to propose a possible definition of the concept of “simultaneous”:
Two events in spacetime are simultaneous if and only if a (mass-possessing) particle cannot move from one event to the other.
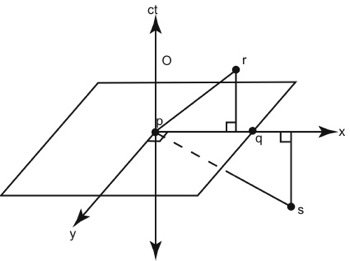
Fig. 2. Simultaneous events in the classical limit for a universe with two dimensions of space and one of time are coplanar.
To illustrate this, let us consider a universe that has only two dimensions of space, and one of time; this way, we can represent the entire spacetime manifold in a 3-dimensional volume with time on the vertical axis, as per standard relativistic diagrams (see fig. 2). In the diagram, a fast moving particle has a nearly horizontal slope because it traverses a lot of space in a short period of time. Conversely, a slow moving particle has a nearly vertical slope since it crosses very little space in a relatively long period of time. A stationary particle is represented by a vertical line. Let us consider a stationary observer (O) at a particular time and place (p), and imagine how this observer would use the above definition to determine which other events in the universe are happening at exactly this same time.
In this diagram, an event p is simultaneous with event q because no particle is fast enough to travel from p to q—this would require infinite speed, which would require infinite energy in the classical limit. Event p is not simultaneous with event r because a particle of the right velocity could travel from p to r. Neither is event s simultaneous with p since a particle can travel from s to p. Moreover, there is no ambiguity about which events have happened first. Clearly events below p and q have happened before p and q, and events higher on the vertical axis have happened later. Any point with the same ct value as p and q is simultaneous with p and q. Thus, in a Newtonian universe with two dimensions of space and one of time, all events concurrent with p are represented by the horizontal plane that passes through p. All observers, regardless of their location or velocity in the universe would agree on both the relative and absolute timing of these events.
Simultaneity in Relativistic Physics
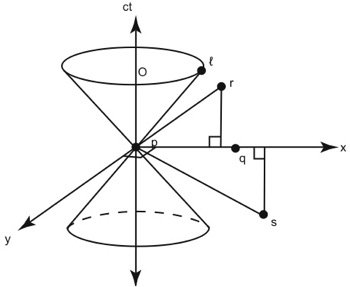
Fig. 3.The finite speed of light divides spacetime into two volumes: space-like, and time-like. Points exactly on the cones are called light-like.
When we consider a relativistic universe the picture becomes far more complex and interesting. Time and space no longer have the objective observer-independent status which they possessed in the Newtonian limit. Most significantly, particles are no longer permitted to have unlimited velocity. Massive particles may have a velocity up to (but not including) the speed of light. The finite speed of light essentially divides spacetime into two domains—the interior and the exterior of the light cones shown in Fig. 3. These cones represent a burst of light emitted from (in the case of the upper cone), or absorbed by (in the case of the lower cone) event p. If we assume axiomatically that light travels at the same speed in all directions relative to an observer, the resulting light path forms two symmetric cones which intersect at their tips at point p. In relativistic literature, events interior to the light cones of p are called “time-like” events (since their separation from p in time is greater than their separation in space), while those exterior to p (such as point s) are called “space-like.” Events on the cones themselves (such as ℓ) are called “light-like” events.
If we consider an event (q) that is space-like relative to p, we find that it fits our previous definition of “simultaneous.” No (finite-mass) particle can travel from p to q, because such a particle would have to travel faster than light, which is not possible for particles with finite rest mass. Even light is not sufficiently fast to reach q from p. The region of simultaneity is no longer a plane as it was in the classical limit, but is (potentially) the volume external to the light cones of event p. Thus, q and p can be considered simultaneous. Likewise, event r can be considered simultaneous with event p, since no particle can travel from one to the other.
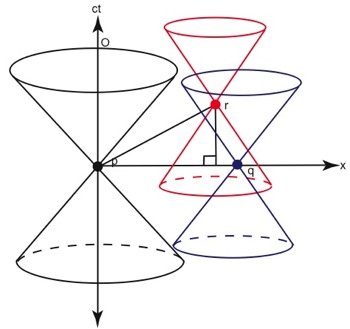
Fig. 4. Although r can be considered simultaneous with p, and q with p, r cannot be simultaneous with q since r lies within the light-cone of q. Event r is time-like with respect to q.
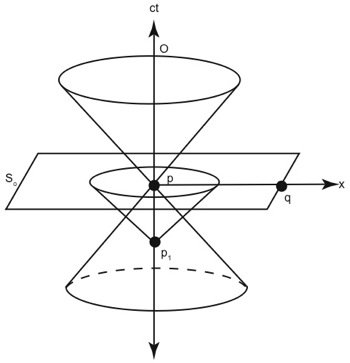
Fig. 5.The assumption that the one-way speed of light is isotropic leads to a definition of simultaneity for event p that is the plane S0.
However, when we consider the light cones of events q and r, we find that an inconsistency arises. These events (q and r) are inside the light cone of each other (see fig. 4). Although they are space-like with respect to p, they are time-like events with respect to each other. A finite-mass particle emitted from q will reach r if it has the right velocity. Therefore, although q is simultaneous with p by our working definition, and although p is simultaneous with r, we find that q is not simultaneous with r, and in fact is unambiguously before r. Since q is in the past light cone of r, and r is in the future light cone of q, it seems inconsistent to call them simultaneous, even from the perspective of a third point (p). This leads us to seek a better definition of “simultaneous.”
To eliminate the above inconsistency, we will need to select a 2-dimensional subset of points from our 3-dimensional volume of spacetime that is external to the light cones. This subset we will define as the set of events simultaneous with p (see fig. 5). This new definition will ensure that no event is within the light cone of any other simultaneous event, thereby guaranteeing that causes always happen before effects in all reference frames. If we again take as an axiom that light travels the same speed in all directions relative to an observer, then it follows that a plane (S0) which is orthogonal to the light cone axis (ct) will represent the set of events that are simultaneous with p. This is because plane S0 is the only plane passing through p in which a light cone from an event at the same location as p but at an earlier time (p1) intersects as a circle. The circle indicates that light from this previous event has traveled the same distance in all directions in the same amount of time. In other words, if and only if we define plane S0 as the set of points that are simultaneous with p, will we find that light travels the same speed in all directions, which is our starting axiom. An event that happens at a later time in the same location (q) will be simultaneous with all events defined by the plane S1 (see fig. 6).
The Relativity of Simultaneity
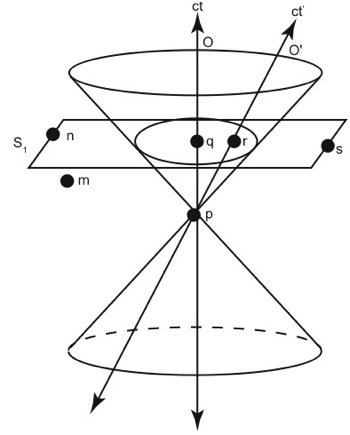
Fig. 6.All events on plane S1 are simultaneous with events q and r as observed by O.
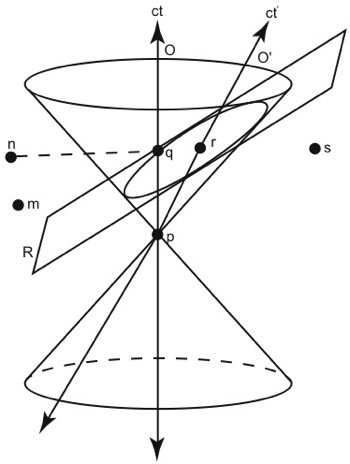
Fig. 7. All events on plane R are simultaneous with r as observed by O’.
What we have done in the above is to define our coordinate system in a particular way. Specifically, we have defined “simultaneous events” in such a way that light by construction propagates at the same speed in all directions relative to the observer. This is called the “Einstein synchrony convention” and represents what is normally done in Relativistic physics. It may seem at first that this gives us a perfectly self-consistent and objective definition of simultaneity. However, when we consider an observer that is moving relative to event p, we will see that this definition of simultaneous is not invariant, but is reference-frame dependent. In Relativistic physics, a “reference frame” is an observer or set of observers that all move at the same constant velocity (same speed and direction) through space. Every observer is allowed to consider himself stationary; the position and motion of all other objects in the universe is based on a coordinate system where the observer is axiomatically always at the origin of the spatial coordinates. The path of the observer (O) through spacetime is simply his own time axis (ct).
Consider another observer O’ that is moving relative to O, but happens to be in the same place at time = 0. That is, both observers pass through event p. At a later time, there will be some distance between O and O’ such that O passes through event q, whereas O’ passes through event r. At q, observer O will conclude that all events in plane S1 are simultaneous with q because the light cone intersects that plane as a circle with q in the center. However, observer O’ will not come to the same conclusion. The circle of intersection between the light cones and plane S1 is not centered on r. Therefore, light would not be traveling the same speed in all directions relative to observer O’ if S1 represented his plane of simultaneity, which would violate our starting axiom that light propagates in an isotropic fashion relative to any observer.
Instead, observer O’ will conclude that the plane R (see fig. 7) represents the set of points that are simultaneous with r, because this plane intersects the light cones in such a way that the observer is in the center.3 In other words, plane R is the plane in which light has traveled the same speed in all directions relative to observer O’. This leads to some interesting consequences. Observer O would conclude that event s and event q are simultaneous, and event m happens before event s since event m is below the plane S1 and therefore has a smaller value for the time (ct) coordinate (as shown in fig. 6). However, observer O’ would conclude that event s and event q are not simultaneous; event s happens before event q since event s is well below the plane R and event q is slightly above (as shown in fig. 7). Moreover, observer O’ concludes that event m happens after event s since m lies above the plane of simultaneity (R) whereas s lies below. The Lorentz transformations can be used to convert from the coordinate system of O to the coordinate system of O’ and vice versa. The important thing here is that not only do O and O’ disagree on whether or not events are simultaneous, they cannot even agree on the order in which events take place! This well-studied phenomenon is called the “relativity of simultaneity.”
Paradoxes like this occur because we intuitively expect space and time to be observer-independent. But the universe simply is not that way. The coordinates by which we measure spatial extents and temporal intervals are fundamentally observer-dependent, and hence there will always be a range of possible values when we assign coordinates to any spacetime event. The relativity of simultaneity is well-known and is covered more rigorously in most introductory textbooks on Special Relativity. Although Einstein synchronization is well-defined and self-consistent for any one reference frame, it is not possible to construct a synchrony definition that is objectively the same for all velocity reference frames at all locations.
Considerations on the Creation Week
The relativity of simultaneity is rarely discussed in creation-based literature. And yet it is crucial to the construction of biblically-based cosmological models. Let us suppose for the sake of argument that the description of the creation of the universe in Genesis is using Einstein synchronization; that is, the way God describes the timing of events is the same system astronomers and physicists use today. Most creationists implicitly assume this. Since the creation of the celestial objects (the lights of the heavens) occurs on the fourth day, all stars were created simultaneously, or nearly so (within 24 hours). But we’ve just seen that what is considered “simultaneous” is relative to the observer’s reference frame. Since God is omnipresent, what reference frame would He choose? The reference frame of the earth is the obvious choice, since the days of creation are described in terms of earth rotations (“the evening and the morning were the Xth day”). Moreover, since the Bible is written for human beings, it stands to reason that the planet on which all humans live would be the reference frame God would use for all time-stamping.
However, the reference frame of the earth changes throughout the year as the earth orbits the sun. Its direction of velocity is constantly changing. So, if the creation of the stars is simultaneous relative to earth on Day Four (as measured by Einstein synchronization), then it cannot be simultaneous relative to earth only sixth months later (when the earth is on the opposite side of the sun, and moving in the opposite direction). In fact, the spread of time becomes enormous when we consider the most distant galaxies.
For example, consider a galaxy 13 billion light years away. And imagine that it is located in the opposite direction that the earth (in its orbit around the sun) was moving during the Creation Week. Then if this galaxy is created on the fourth day according to the Einstein synchrony convention, we find by the Lorentz transformation that six months later (when the earth is moving toward this galaxy) it would have been created 2.6 million years before the earth!4 Perhaps even more strangely, if we consider a galaxy in the opposite direction (such that earth is moving toward it at its creation), also 13 billion light years away and created on Day Four, the Lorentz transformation tells us that this galaxy from earth’s reference frame six months later will not have been created yet! Its creation will be 2.6 million years in the future.
This effect is illustrated in Figs. 6 and 7. Observer O represents earth at its creation. Event s represents the creation of the first galaxy we considered, and event n represents the second galaxy we considered. Plane S1 represents the entire universe at that time (that is, Day Four). We see that event s and event n (the creation of those two galaxies) occur on Day Four as expected (see fig. 6). Six months later, the earth has a different velocity frame, and is now represented by O’ (see fig. 7). So, plane R represents the entire universe at that time. We can see that event s now lies in the distant past, indicating that the galaxy was created long ago (2.6 million years ago from the Lorentz transformation). Whereas event n now lies in earth’s future; that galaxy will not be created for another 2.6 million years.
Einstein synchronization is very useful in physics and does have clear advantages over other systems. But, as we have seen, it also leads to some rather strange results. Two cosmically distant events that are considered simultaneous in one reference frame will inevitably be separated by millions of years in another reference frame. More generally, any two space-like events will be considered simultaneous in some reference frame. In other reference frames, one will occur before the other; however, the order in which they occur will be different for different velocity frames. So, if the creation of all the galaxies in the cosmos is simultaneous in one reference frame, it will be spread out over millions of years in another. And the earth is constantly shifting reference frames in its annual orbit.
We could resolve this discrepancy by selecting some other reference frame, one that does not change with time, such as the center of mass of the entire universe. However, this seems rather arbitrary, and biblically unwarranted. Essentially all other time references in Scripture are given in terms of earth time, and in particular, the local time at the location under discussion. Why make an exception for Genesis? This would be nothing more than special pleading. Since the creation days are always bound by morning and evening, it seems clear that the velocity frame used to describe the creation account (and in general throughout the Scriptures) is that of the earth.
Since the creation of the entire universe took place within a timescale of six earth rotation days, we must ascertain what synchrony convention God is using when He speaks of the stars being created on the fourth day. We have seen that if we assume that this is the fourth day as measured by Einstein synchronization, then creation takes place in six days only when the earth is moving at a particular speed in a particular direction. Thus, those six days become spread out over millions of years when the earth changes direction in its annual orbit. But there is no hint of such a thing in Scripture. The Bible only ever speaks of creation taking place in a short span of time (six days) regardless of when the statement is made (for example, Genesis 1; Exodus 20:11; Mark 10:6). Moreover, the fact that the creation of some galaxies lies in the distant future when measured by Einstein synchrony seems to clash with Genesis 2:1–2, which indicate that God’s work of creation is finished and that God is no longer creating. The Einstein synchrony convention seems to create a number of inconsistencies when applied to Genesis 1. Might this suggest that the Bible does not use Einstein synchronization? This leads us to ask whether there may be an alternative definition of simultaneity in which creation takes place in six days regardless of the earth’s velocity at other times.
Alternative Synchrony Conventions
The Einstein synchrony convention that we have been working with so far is based on two axioms. First, if a (massive) particle can travel from event A to event B, then the two events are not simultaneous. This criterion is necessary to preserve cause-and-effect relationships and eliminates the volume within the light cones. Second, in order to eliminate any remaining ambiguity, we selected only a 2-dimensional subset of the remaining points: the plane in which the light cone intersects as a circle. This is equivalent to assuming that light travels at the same speed in all directions relative to any observer. We chose this for simplicity. However, this second axiom is not actually a requirement or premise of Special Relativity (Einstein 1961). Relativity only requires that the two-way time averaged speed of light is constant for any observer. Although Einstein synchrony is normally used as the particular system in which the equations are expressed, it is not a requirement. By dropping this second axiom, we find that there are alternative definitions of simultaneity that are logically consistent for any given observer.
In principle, we could select any two-dimensional manifold exterior to the light cones of p, providing that no point in this manifold is within the light cone of any other point. Any such definition of simultaneity will be self-consistent for any given observer and will preserve causality. For example, we could select planes of simultaneity that are tilted relative to the light cones. Such a definition is equivalent to assuming that light travels at different speeds in different directions. This is permitted in Relativity, provided that the round-trip speed is constant for any observer. In fact, it has been shown that Special Relativity can be expressed using non-Einstein synchrony conventions, leaving the one-way speed of light as a free parameter (Winnie 1970a, b).
Therefore, an infinite number of such synchrony conventions may be stipulated. However, not all such selections will be particularly useful. But there is one that is especially useful. Let us consider a non-Einstein synchrony convention in which all points in the past light cone of p are considered simultaneous. This convention has been used in the technical literature (Sarkar and Stachel 1999). Moreover, Einstein himself considered using this convention, but preferred to use the standard convention because it is position-independent (as we will see shortly). To avoid having causally-connected simultaneous events, we could move the cone infinitesimally outside the past light cone as follows.
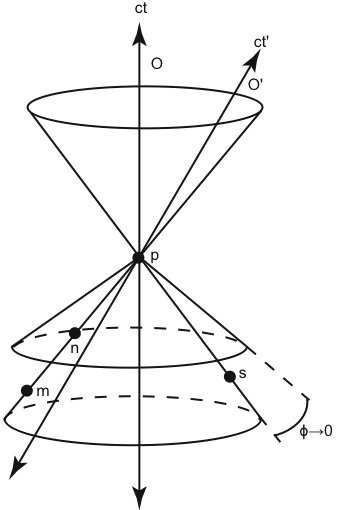
Fig. 8.A cone surrounding the past light cone of p at an infinitesimal angle ϕ is defined as those events simultaneous with p.
We define “simultaneous” as the set of events that form a cone around the lower (past) light cone of p at angle ϕ where ϕ represents an infinitesimal quantity (see fig. 8). For all practical purposes, we are using the lower light cone as the surface of simultaneity; except I am displacing it by an infinitesimal amount (ϕ) in order to ensure that simultaneous events are always space-like rather than light-like, thereby making them causally unconnected. This is an anisotropic synchrony convention (ASC) because we are stipulating that light travels at different speeds depending on its direction or position relative to observer O. It is clear that this definition fits our criteria. First, no positive-rest-mass particle can travel from any event on this cone to any other. Second, no point on this cone is within the light cones of any other point. Although ASC lacks the mathematical symmetry of the Einstein convention, it has certain interesting advantages.
Notice that since events p, m, n, and s are on the surface of the cone (or infinitesimally exterior to it), they are all considered simultaneous under the ASC definition. Moreover, since observer O’ shares the same light cones as observer O at point p, this means observer O’ also considers events p, m, n, and s to be simultaneous. This is a unique feature of ASC: observers at the same location all agree on which events are simultaneous—regardless of the velocity of the observer. Recall that the Einstein synchrony convention lacks this feature; two observers at the same location will (in general) disagree on which events are simultaneous if the observers have different velocities. The Einstein synchrony convention requires that two observers have the same velocity (not position) if they are to agree on which events in the universe are simultaneous. Apparently, a preference for a position-independent synchrony convention rather than a velocity-independent one was the reason that Einstein himself preferred to use the convention that now bears his name (Sarkar and Stachel 1999).
Implications of Describing Creation using ASC
If we suppose for argument’s sake that the Bible uses the anisotropic synchrony convention (ASC) as defined above when describing the timing of events, we find that this eliminates the problems we encountered under the Einstein synchrony convention. Recall that under Einstein synchronization the creation of the distant stars is instantaneous when earth is on one side of its orbit; however, that creation becomes spread out over millions of years only six months later. This occurs because of the difference in velocity of the two reference frames as computed from the Lorentz transformation. However, with ASC, the velocity does not matter. Both earth at creation (O) and earth six months later (O’) have approximately the same position, even though the velocity is quite different. Therefore, under ASC, both would consider the creation of the stars to be simultaneous on Day Four—even for the most distant galaxies.
Most significantly, ASC reduces the inward-directed light travel-time to zero. Since ASC defines simultaneity as being infinitesimally close to the past light cones, it follows that the creation of a star on Day Four happens at essentially the same time as the light from that star reaches earth. Under ASC, the “distant starlight problem” disappears. Even the most distant galaxy is created on Day Four, and its light reaches earth effectively simultaneously on Day Four. Of course, the fact that ASC solves the distant starlight problem does not ipso facto mean that it is the convention that the Bible uses. Nonetheless, we have seen thus far that (1) if the Bible does use ASC to mark time in Genesis, then (2) the distant starlight problem is solved. Part 1 of this proposition remains to be proved. However, we are already seeing a strong suggestion that it may be so, since ASC eliminates the problem of the de-synchronization of the Creation Week that occurs when the Lorentz transformation is applied to earth’s annual orbit.
Synchrony Conventions and the One-Way Speed of Light
Both theory and experimentation confirm that the round trip speed of light in a vacuum is constant relative to any inertial observer.5 So, if we take light and bounce it off one or more mirrors so that it returns to its source location, the time it takes will be constant for a given distance (for any inertial observer who performs the experiment) and is given by L/c where L is the total length of the path and c is the (round trip) speed of light. However, the speed of light in any one direction is not necessarily constant. As counter-intuitive as it may seem, the one-way speed of light is not a constant of nature, but is a matter of convention. It is something we may choose, providing that our choice preserves causality, is self-consistent, and providing the round trip speed of light is still exactly c.
The act of choosing a synchrony convention is synonymous with defining the one-way speed of light. If we select Einstein synchronization, then we have declared that the speed of light is the same in all directions. If we select ASC, then we have declared that light is essentially infinitely fast when moving directly toward the observer, and ½c when moving directly away. Under ASC, the speed of light as a function of direction relative to the observer (θ) is given by cθ = c/(1-cos(θ)), where θ = 0 indicates the direction directly toward the observer.
It seems counter-intuitive that we may simply stipulate the one-way speed of light. It seems that the one-way speed of light should be unambiguous and measurable, in which case we would not have the freedom to choose an alternate synchrony convention. However, this is not so. We should remember that people once thought that durations in time and lengths in space were objective and unambiguous, irrespective of the observer’s velocity. But Einstein’s discoveries rule out such possibilities. In the next two sections, I will show that the one-way speed of light is conventional. It is something that is stipulated by us, and is not an independent measurable property of the universe. This will be only a brief review of what is often called the “conventionality thesis.” More thorough treatments are available in the technical literature (Salmon 1977; Winnie 1970a, b).
Attempts to Measure the One-Way Speed of Light
Measuring the round-trip average speed of light is quite easy in principle. We could set up a clock at location A and a mirror at location B which is distance S from A. We send out a light beam from the clock at location A; the beam reflects off the mirror at B and returns to A. We subtract the time when the light left from the time when it returned and call the difference t. The round trip time-averaged speed of light is then given by c = 2S/t.
We could attempt to measure the one-way speed of light by a similar experiment. But since the light is no longer on a closed path, we will now need another clock at B to record the time at which the light arrives. The time of light arrival at clock B minus the time of light departure at clock A is t. The one-way speed of light would seem to be cθ = S/t. But there is a catch. In order for us to obtain the correct answer we must be certain that clock B is synchronized with clock A—that both clocks read the same time at the same time. This seemingly trivial task turns out to be surprisingly difficult.
How do we synchronize clock B with clock A? Suppose that we send out a radio signal from clock A when it strikes noon. Clock B is then set to noon when it receives this signal. But the problem here is that the radio signal has taken some time to travel from A to B. So, perhaps we should set clock B a bit ahead of noon, when it receives the signal. But how far ahead should we set it? This of course will depend on the amount of time it took the radio pulse to travel from A to B. Radio waves travel at the speed of light. But the one-way speed of light is the very thing here in question. So, we would have to know the one-way speed of light in advance in order to synchronize clock B with clock A, in order to measure the one-way speed of light. The catch-22 is clear.
Other types of signals suffer from the same problem. All other types of signals directly or indirectly depend upon the one-way speed of light. For example, sending an electrical signal from A to B to synchronize the clocks does no good, because electricity travels at essentially the speed of light, which is the quantity in question. Even sound signals are dependent on the one-way speed of light, because the collision of atoms is an electromagnetic interaction; and electromagnetic fields propagate at the speed of light.
Another way in which we might attempt to synchronize clocks at A and B is to bring the clock at B to A and synchronize the two at the same location. This eliminates any ambiguity due to light travel time. We then move one of the clocks to point B. It’s simple enough, but there is again a catch. Einstein tells us that motion affects the passage of time. So, although the two clocks were indeed synchronized when they were together, the very act of moving one clock to B has caused it to become desynchronized with the clock at A. How much it is off will depend on the one-way speed of light, the very issue in question.
Slow Clock Transport
Some people have proposed a method by which we might overcome the difficulty of synchronizing clock B with clock A. Since motion affects the passage of time, if we were to synchronize two clocks at point A and then move one clock to B and then back to A, the two clocks would no longer read the same time. If we repeated this experiment but moved clock B much more slowly, we would find that it would be much closer to synchronization with clock A, though still not exactly.
Although we will not repeat the proof here, it is a consequence of Special Relativity that clock B will be exactly synchronized with clock A if we do this experiment in the limit as the velocity of clock B goes to zero (Salmon 1977, p. 264; Winnie 1970a, pp. 96–97). In other words, clock B will be very nearly synchronized with clock A as long as we move it as slowly as possible. Based on this, some have suggested that slow clock transport will allow us to synchronize clocks separated by a distance. Simply synchronize clock B to clock A when the two clocks have the same location. Then move clock B to a distant location as slowly as possible, and (it is claimed) it should still be synchronized with clock A.
As reasonable as this may sound, there is a fundamental flaw in the method; a critical assumption has been made. We know from Special Relativity that a clock moved slowly will still be synchronized with its stationary counterpart when moved back to the original position (in the limit of zero velocity). However, we have merely assumed that it remained synchronized throughout the journey. In other words, how do we know that clock B did not lose ten minutes when moved to its distant position, and then subsequently gain ten minutes when moved back to clock A? It could very well be that outgoing clocks experience time differently than incoming clocks. Special Relativity only requires that the net effect adds to zero when clock B returns home in the limit of zero velocity (Winnie 1970a, pp. 96–97). The amount by which clock B becomes desynchronized as it gains distance from A can be computed, but only if the one-way speed of light is known in advance.
In all cases, the one-way speed of light must first be stipulated before we can construct any experiment to measure it. Therefore, at best, such experiments can only show consistency. But they show consistency for many different synchrony conventions. If we synchronized two distant clocks using the Einstein synchrony convention, and then used these clocks to measure the one-way speed of light, we would find that it is the same in all directions. This result is hardly surprising since we have assumed this at the outset. The very method of Einstein synchronization implicitly presupposes that the speed of light is the same in all directions.
If we were to repeat the experiment, this time synchronizing our clocks by ASC, then we would find that the speed of light is different in different directions—confirming (but not proving) our starting presupposition. Such experiments cannot therefore ever actually test the one-way speed of light without first stipulating it. The results are self-consistent; but other definitions of simultaneity also lead to self-consistent results. Although there have been attempts to refute the conventionality thesis, so far all such attempts have subtly presupposed Einstein synchronization as the method by which the two clocks are synchronized; hence, they have begged the question and are not cogent refutations (Sarker and Stachel 1999).
Einstein himself noted that attempts to measure the one-way speed of light are inherently circular. In discussing the simultaneity of two bolts of lightning at A and B, as perceived by a person standing exactly in between them at M, he says,
. . . if only I knew that the light by means of which the observer at M perceives the lightning flashes travels along the length A → M with the same velocity as along the length B → M. But an examination would only be possible if we already had at our disposal the means of measuring time. It would thus appear as though we were moving here in a logical circle. (Einstein 1961, pp. 22–23).
Einstein rightly concludes that the one-way speed of light is not an empirical quantity of nature, but a choice of man. He states,
That light requires the same time to traverse the path A → M as for the path B → M is in reality neither a supposition nor a hypothesis about the physical nature of light, but a stipulation which I can make of my own freewill in order to arrive at a definition of simultaneity (Einstein 1961, p. 23) [emphasis is in the original].
This conclusion is quite profound. Since we cannot (even in principle) ever measure the one-way speed of light, Einstein concludes that the one-way speed of light is not actually a property of nature, but a choice of man. Before Einstein, we might have assumed that the one-way speed of light (and thus, the corresponding synchrony convention) is a property of the universe—one that we are not clever enough to measure. But according to Einstein, the fact that we can never test a synchrony convention shows us something fundamental about the universe. Namely, it tells us that synchrony conventions are not a property of the universe, but are instead a system of measurement invented by man. According to the conventionality thesis, no experiment will ever be able to establish one synchrony convention over another, because synchronization systems are a human invention by which we measure other things—much like the metric system.
The Motivation for Selecting a Synchrony Convention
The above thought experiments demonstrate that nature does not prefer one synchrony convention over another any more than nature prefers the metric system over the English system. We may choose to work in the metric system, but we can always convert to another system. Likewise, we may freely stipulate the one-way speed of light (within certain constraints) and synchronize clocks accordingly. However, there are good reasons for selecting one convention over another depending on the circumstances. Though the Bible may use ASC exclusively (I will make an argument for this shortly), this does not mean that we must also use ASC in all circumstances. After all, it would be absurd to say that we cannot use “meters” or “yards” on the basis that the Bible uses “cubits.”6 Einstein synchronization does have its place. In particular, Einstein synchronization is isotropic; the speed of light is stipulated to be the same in all directions. This greatly simplifies the equations of Special Relativity, thereby making Einstein synchronization the preferred convention to be used when doing physics computations.
Much as the metric system is easier to use in physics calculations than the English system, no one would suggest that students learning Special Relativity for the first time should use anything other than the Einstein synchrony convention. One consequence of the Einstein synchrony convention is that all observers agree on the timing of distant events if the observers have the same velocity—regardless of the position of the observers. Conversely, ASC would have all observers agree on the timing of events if the observers have the same location, regardless of velocity. Since Relativity is concerned with velocity reference frames, it is very useful to select a synchrony convention in which velocity alone (irrespective of location) sets the timing of distant events. The mathematical advantages of the Einstein synchrony convention are clear.
And yet, mathematical advantage is not the only consideration when selecting a synchrony convention. The focus of this paper is to discern what convention the Bible is using, not which convention should be used in introductory physics textbooks. Indeed, the Bible does not always select the convention that modern physicists would prefer. For example, consider the timing of events on earth. Events on earth can be measured in terms of local time (the time as defined by our local time-zone), or universal time (the standard time in Greenwich, England). A scientist measuring the speed of an aircraft (one that crosses several time zones) would no doubt use universal time. And yet the Bible uses local time (not identical to our time-zones, but similar), more or less exclusively. The primary purpose of the Bible is to communicate as clearly as possible, in a way that reaches all people-groups at all times, not just modern physicists. To best accomplish this purpose, the anisotropic synchrony convention is superior to the Einstein synchrony convention. Thus, it seems very likely that the Bible uses ASC. Let us consider some of the advantages of ASC in terms of communicating truth to all cultures at all times.
The Biblical Basis for ASC
Note that ASC has definite observational advantages over the Einstein synchrony convention. Of all the infinite possible synchrony conventions, only ASC does not require knowledge of the distance to the source to record the time of any event. Since the surface of simultaneity is essentially identical with the past light cone, events happen as they are seen. Any other synchrony convention requires (1) knowledge of the distance to the source, and (2) knowledge of the speed of light (or at least the stipulation of its one-way speed), in order to compute the light-travel-time from the object to the observer. The resulting number is then subtracted from the time the event was observed, to find the time when the event happened. But since the (inward directed) light-travel-time of ASC is axiomatically zero, there is no need to know the distance to the source, nor the round-trip speed of light.
As far as we know, ancient cultures did not know (1) the distance to any star (aside from perhaps the sun, and then only very roughly), nor (2) the speed of light (either in one direction, or the round trip speed). Thus, it appears that all ancient cultures on earth implicitly used ASC. The time when a celestial event is seen was considered to be simultaneous with the time in which the event happened. It is also noteworthy that modern astronomers also use ASC (implicitly), for example, when naming supernovae. A supernova (such as 1987A) is always named for the year in which its light reaches earth—the anisotropic synchrony convention.
Einstein synchronization only became widely used in the twentieth century, and only in educated parts of the world. Given that ASC has been the standard for all other times and cultures, it makes sense that the Bible would use ASC when communicating the timing of celestial events. The perspicuity of Scripture (the principle that the Bible is clear and meant to be understood by all cultures at all time periods) strongly suggests a synchrony convention that would be understood by all cultures at all times, rather than a synchrony convention that would only be used by academics in the twentieth and twenty-first centuries.
Perhaps most significantly, Scripture itself seems to suggest that the creation of the stars was nearly simultaneous with their light reaching earth. Genesis 1:14–15 describes the creation of the celestial lights, and gives their purpose: to be for signs, seasons, days, and years, and to give light upon the earth (Genesis 1:15). Verse 15 also states, “and it was so” indicating that the stars immediately functioned in their God-ordained role: to give light upon the earth. This strongly implies that the Bible is using the anisotropic synchrony convention—the only convention in which all events are effectively simultaneous with their light reaching the observer.
If the above analysis is correct and the Bible is indeed using ASC, then the distant starlight problem is resolved. The starlight problem was not so much a physics problem, but an error of exegesis. It is the semantic anachronism fallacy (Carson 1984). This is the fallacy of reading a modern meaning into an ancient term. In this case, people have been reading Genesis as if it were using the modern Einstein convention, rather than the more ancient and more common ASC. Since it now strongly appears that the Bible is using ASC, starlight from the most distant galaxies will naturally reach earth essentially instantaneously on the fourth day of creation.
It may seem a strange result to those unfamiliar with Special Relativity. However, it is already well-established that clocks tick slower as they approach the speed of light, and would stop completely if they could attain the speed of light. So, from light’s point of view (imagine that we could travel alongside the light) every trip is instantaneous anyway. This happens regardless of which synchrony convention we use. So, it is not so surprising that we can find a synchrony convention where the travel time is also zero as measured by observers on earth.
In light of this, it seems that distant starlight cannot be legitimately used as an argument against the biblical timescale. The critic cannot even begin to construct an argument based on starlight travel-time unless he can first show that the Bible does not use ASC or some equivalent synchrony convention. Of course, there are many other things the critic would also have to demonstrate about the nature of light, spacetime, and so on. The point here is that his argument cannot have any merit whatsoever until he at least deals with synchrony conventions and attempts to refute the claim that the Bible uses ASC.
Potential Objections to the Anisotropic Synchrony Convention
Although it is impossible to anticipate all potential objections to the above analysis, I will here discuss some of the more obvious possibilities.
(1) Consider the person who says, “But if the Bible really indicates that God created in six days by ASC, then when we convert ASC to Einstein synchrony, it would mean that God really created over millions of years. It means that He made the stars long before the earth so that their light would reach earth on Day Four. But then God didn’t really create in six days.” Such an objection fails for several reasons. First, it contradicts the conventionality thesis. The objection subtly presupposes that the Einstein synchrony convention marks the “true” time, and that ASC does not. However, the conventionality thesis tells us that ASC marks the “real” time of an event just as much as does Einstein synchrony. According to Einstein, there is no “true” time if by that we mean an objective universal synchrony convention that doesn’t depend on position or velocity. The person who argues otherwise has slipped into non-Einstein thinking. ASC is a perfectly legitimate synchrony convention. Therefore, God really did create in six ordinary days, and the light really did reach earth on Day Four.
Second, even if the conventionality thesis were refuted, this objection still fails because the issue is not “which convention does nature prefer?” but rather “which convention does the Bible use?” If someone could show that ASC is merely a phenomenological convention, this would not invalidate the Bible’s use of it. Sunrise and sunset are phenomenological, and the Bible does use them in that way. To be clear, I do not believe that ASC is phenomenological.7 But even if it were, the critic must still show that the Bible is not using ASC, but is using Einstein or some other synchrony convention in which light-travel-time is not instantaneous.
Third, while it is true that converting from six days in ASC to the Einstein synchrony convention will give billions of years, we should also consider the reverse: Converting from six days in the Einstein synchrony convention to ASC will also give billions of years. So, the critic’s objection is completely reversible, and therefore not legitimate. The real issue is not age per se, but rather what does the Bible teach?
(2) “But maybe light really does travel the same speed in all directions. You don’t know for sure that it doesn’t. So, ASC could potentially be wrong.” This objection also denies the conventionality thesis. Those unfamiliar with Relativistic physics are deeply inclined to believe in absolute time and space. And therefore, it will seem strongly intuitive to them that the one-way speed of light should be an objective, invariant, and measurable quantity. But the universe is not constructed that way. For whatever reason, God has constructed the universe in such a way that length, duration, and synchronization are relative to a given observer. Our inability to measure the one-way speed of light is not due to a lack of creativity on our part in designing some experiment to do it. Rather, it is due to the way God has constructed spacetime. Consequently, the one-way speed of light must be stipulated at the outset.
(3) “If God made things such that their light reaches earth on Day Four, then He must have made them millions of years before earth. But Exodus 20:11 indicates that God created everything within six days.” This objection is fallacious because it begs the question. Only in the Einstein synchrony convention would God have made the celestial sources long before earth such that their light reaches earth on Day Four. In ASC, the stars are made on Day Four of the Creation Week, and their light reaches earth essentially instantaneously. This criticism implicitly assumes that the Bible uses the Einstein synchrony convention in Exodus 20:11 to argue that the Bible must use that convention in Genesis. But such an assumption is unwarranted. We have seen previously that there are good reasons to think that the Bible uses ASC throughout—including Exodus 20:11.
(4) “ASC is more mathematically complex than the Einstein synchrony convention. Therefore, by Occam’s razor, Einstein synchrony is more likely to be correct.” This objection also fails for two reasons. First, Occam’s razor applies to competing models, not alternative conventions. It would be ridiculous to argue that the metric system is more likely to be “correct” than the English system on the basis that it is mathematically simpler. A system of measurement cannot be “correct” or “incorrect”, though it may be “useful” or “not useful.” Likewise, the Einstein synchrony convention and ASC are two different systems of measurement (like English units and metric), and one can be converted to the other. They are not competing models.
Second, by arguing that one measurement system is “correct,” this hypothetical critic exhibits non-Relativistic thinking. He has denied the conventionality thesis in which we understand that both ASC and Einstein synchronization are legitimate synchrony conventions in Special Relativity. Even for those people familiar with Relativity, it is all too easy to slip back into pre-Einstein thinking, in which we intuitively feel that the one-way speed of light (and hence a given synchrony convention) can be “true” or “false.” But that simply isn’t so. Synchrony conventions are stipulated. They are not a property of the universe that can be investigated.
The ASC Model
The anisotropic synchrony convention is just that—a convention. It is not a scientific model; it does not make testable predictions. It is a convention of measurement and cannot be falsified any more than the metric system can be falsified. However, I have made an argument in this paper that the Bible uses the ASC system. This claim is in principle falsifiable, though of course I have argued that it is true. Furthermore, given the information in Genesis and the inference that the Bible does use ASC, we can construct a cosmology that does make testable predictions. I will refer to this as the “ASC model.”
To be clear, the ASC convention does not make testable predictions and cannot be falsified. However, the ASC model goes beyond the mere convention and does make testable claims and is therefore falsifiable. The essential claim of the ASC model is that the Bible uses the ASC convention. Depending on which additional assumptions we make, we could actually construct a number of different ASC models which make different testable predictions about the way the universe should appear today. These will all have certain features in common because—by definition—they all presume that the Bible’s description in Genesis is accurate and is using the anisotropic synchrony convention.
We now consider some additional reasonable assumptions upon which we can construct the ASC model. Let us suppose first of all that the effects of gravitational time dilation in the universe are relatively small. Einstein’s General Relativity tells us that gravitational potential affects the passage of time. However, the effect is quite small except near the surface of a neutron star or a black hole. Based on the estimated mass in the visible universe, and the distance to the galaxies, the gravitational potential between earth and the farthest known galaxies is small enough that it produces only a nominal amount of relativistic time dilation. So we have a good reason for making this assumption.
I am aware that there are young-universe cosmologies which suppose that the effects of gravitational time dilation are, or at least were at some point in the past, extremely large (Humphreys 1994). In principle, ASC is perfectly compatible with a large degree of gravitational time dilation; however, such dilation is not required in the ASC model. Thus, the ASC model I propose here will presume that gravitational time dilation is negligible. This may turn out not to be the case, in which case the model will need to be modified. But it seems the simplest interpretation of the data at the moment.8 I will further stipulate that the consensus understanding of galactic distances, redshifts, and universal expansion is basically correct, having been established by good scientific procedures which are verifiable in the present.
Observational Predictions and Confirmations of the ASC Model
Given the above stipulations, we are now in a position to make falsifiable predictions about how the universe should appear. Since the ASC model has the stars being made on the fourth day of the Creation Week, and since light travel-time is zero under the selected synchrony convention, and since we have supposed that gravitational time dilation is negligible, it follows that the universe appears at all distances as it is now, having aged an equal amount everywhere. Therefore, when we look at any region of the universe, we are seeing it at an age of roughly 6,000 years.9 That being the case, we should expect to see indications of the youth of the universe (in contrast to billions of years) at all distances. We should expect to find processes that cannot be easily extrapolated into a billions-of-years hypothetical past, and which consequently place an upper limit on the age of the process that is far less than big bang models would predict. The ASC model predicts that such indicators will be found at all distances within the visible cosmos. It is noteworthy that we already have some confirmation of this.
Consider blue stars. Blue, O-type, stars are the hottest and most luminous stars in the universe. Although they are more massive than their yellow and red counterparts, their high luminosity means that they use up their fuel much more quickly than other stars. The hottest blue stars cannot last more than a million years or so. Moreover, it is well known that spontaneous star formation is riddled with theoretical difficulties (overcoming internal gas pressure, angular momentum, and magnetic fields) and lacks any significant observational support. This is particularly problematic for blue stars since they have the greatest mass. If blue stars do not form, then their presence in any region of space suggests that that region was created in the recent past. Blue stars are ubiquitous in our galaxy, and are apparently in the most distant spiral galaxies as well. This is a strong confirmation of the ASC model. The fact that numerous blue stars exist at all distances is consistent with a universe that is thousands of years old at all distances as we now see it.
Another example is spiral galaxies. It is well known that spiral galaxies rotate differentially, with the inner regions rotating significantly faster than the outer regions. Thus, if any spiral galaxy were more than 1 billion years old, its spiral structure should be so tightly wound that it would no longer be discernable. Yet this is not what we find. Spiral structure is easily visible in most face-on galaxies, indicating the youth of these galaxies regardless of their distance from the solar system.
Secular astronomers have created auxiliary hypotheses to rescue their worldview from this evidence. For example, they suppose that some sort of density waves might trigger star formation in spiral patterns thereby continually creating new spiral structure as the old structure dissipates (Lin and Shu 1964). But such a hypothesis has a number of difficulties (the trigger mechanism, contrary observations like backward-wound spirals, etc.) and presupposes star formation (which has difficulties of its own). So the simplest explanation is that the galaxies are young.
Indeed spiral galaxies nearby strongly resemble those found in the Hubble Deep Field—at the edge of our current knowledge of the universe. The spiral structure is clearly seen in both nearby and distant galaxies, suggesting that they are all roughly the same age as we see them now. This again confirms the ASC model. Even the amount of spiral wrapping seems to be about the same for nearby and very distant galaxies as we see them now—exactly as the ASC model predicts.
The ASC model also makes some predictions that are as yet only partially confirmed. Since the model predicts that all regions of the universe should have aged only a few thousand years as we now see them, it follows that there should be evidence of youth in our own solar system as well as distant stellar systems. Creationists have already pointed out a number of such examples in the solar system. Comets, the internal heat of three of the Jovian planets,10 and strong planetary magnetic fields are all things than cannot last billions of years and yet are found within our solar system. I am aware that secularists have their auxiliary hypotheses to explain these things from within their own worldview. Here I simply mean to show that within a creationist framework these lines of evidence confirm a young solar system.
Of course, evidence of youth within our solar system does not confirm the ASC model over and above other creation models. But it does confirm the ASC model over and above secular models. But unlike some creation models, the ASC model also predicts that such things should exist at great distances within our galaxy, and even in the most distant galaxies in the universe. We have already seen indications of youth in other stellar systems.
As one example, most astronomers would concede that ring systems (such as those surrounding Saturn) cannot last billions of years.11 Yet even now there is evidence that at least some extrasolar planets have such ring systems as well. Fomalhaut b, for example, is suspected to have a massive ring system based on its high brightness in visible wavelengths (Kalas et al. 2010). The planet’s brightness in infrared suggests a high temperature which is also indicative of youth (Kalas et al. 2010). Although Fomalhaut b is one of only a handful of extra-solar planets that have been directly imaged so that we have such brightness and temperature data, and although it is not a very distant world by cosmological standards,12 it at least suggests that other extra-solar planets will exhibit the same indications of youth that we find within our own solar system. Extra-solar planet research is still in its infancy. But the prospect of finding evidence of planetary youth (as the ASC model predicts) in other solar systems both within and beyond our galaxy is very exciting.
Conclusions
The distant starlight problem is resolved if we accept that Genesis is using the anisotropic synchrony convention (ASC) rather than the Einstein synchrony convention. The resolution is simple: under ASC, the one-way speed of light when directed toward earth is axiomatically infinite, even though the round-trip speed of light remains 3 × 108 m/s. Thus, the light from stars that are created on the fourth day will naturally reach the earth essentially instantaneously.
Moreover, we have seen that there are good reasons to suppose that the Bible does indeed use ASC. First, the fact that Genesis implies that the light from stars created on Day Four reached earth on that day (“and it was so”) naturally implies the ASC convention. Second, such a convention was the only one available to the ancient world. Thus, if the Bible really is designed to communicate truth to all people-groups at all times then ASC is the obvious choice. The Einstein synchrony convention was not in common use until the early twentieth century, and so it makes little sense for God to use such a convention in the Scriptures. Third, we have seen that the Einstein convention is heavily dependent on the observer’s state of motion. Thus, events that are simultaneous in one velocity frame will be spread over millions of years in another. Even the earth’s annual orbit would cause the Creation Week to become millions of years long.13 There is no hint of this in Scripture, thereby suggesting that the Bible does not use the Einstein convention. Indeed, the problem disappears when we use ASC.
We have seen that synchrony conventions amount to a choice of coordinate system. They are stipulated on the basis of their usefulness. They are not a hypothesis; they are not something that can be “tested” for truthfulness. Stipulating a synchrony convention is mathematically equivalent to stipulating the one-way speed of light. Though it may seem counter-intuitive to those unfamiliar with Relativity, the one-way speed of light cannot be measured without first stipulating it either explicitly or implicitly. In the same way that we cannot test whether the English system or the metric system is “correct,” so we cannot test the one-way speed of light. It is chosen as a matter of convention.
There are an infinite number of possible synchrony conventions. However, two of them turn out to be extremely useful. The Einstein (standard) synchrony convention has the advantage that two observers with the same velocity will agree on which events are simultaneous (regardless of position). The anisotropic synchrony convention has the advantage that two observers with the same position will agree on which events are simultaneous (regardless of velocity). Since Relativity is primarily concerned with velocity frames, it is normally formulated according to the Einstein convention in which the equations take on their simplest form due to symmetry.
However, Relativity can be (and has been) formulated in non-Einstein synchrony conventions (Winnie 1970a, b). Indeed, Einstein himself pointed out that it would be possible to stipulate that the past light cone is the surface of simultaneity, just as ASC does. He states:
We could content ourselves with evaluating the time of events by stationing an observer with a clock at the origin of co-ordinates, who assigns to an event to be evaluated the corresponding position of the hands of the clock when a light signal from that event reaches him (Sarkar and Stachel 1999).
He ended up choosing to formulate Relativity in the standard synchrony convention, not of necessity, but because it has the advantage of being independent of the position (rather than the velocity) of the observer. Of the anisotropic synchrony convention Einstein states that it “has the drawback that it is not independent of the position of the observer with the clock” (Sarkar and Stachel 1999). However, there are other factors that make ASC the superior choice for best preserving the perspicuity of Scripture.
The potential objections to ASC covered above are found to be unwarranted. Most of them deny the conventionality thesis. Many of them beg the question by presupposing that only Einstein synchronization is acceptable, and then arguing that alternatives are unacceptable. Moreover, even if the conventionality thesis were refuted, the critic would still have to show that the Bible cannot be using ASC as a convenient phenomenological system. It is my judgment, however, that the case for the conventionality thesis is quite strong, and cannot be refuted without begging the question.
By merely accepting the ASC as a convention, the distant starlight problem is resolved. However, by making a few additional, reasonable assumptions, we are able to produce a basic model of cosmology—the ASC model. This model makes falsifiable predictions, many of which have already been confirmed. The ASC model implies that all regions of the universe have aged only a few thousand years as we now see them. This prediction is contrary to most other starlight models, including time-dilation models. Yet, the prediction has some observational support, such as the detection of blue stars and spiral galaxies at all distances.
We note that the ASC model only accounts for distant starlight and other earthward-directed phenomena that move at nearly the speed of light (such as neutrinos). It has been suggested that other celestial phenomena require billions of years: collisions of galaxies, jets of material from active galactic nuclei (AGNs), etc. However, I do not believe this is so. It seems to me that the mature creation argument works quite well on distributions of matter. Unlike light, the supernatural creation of matter in a specific configuration does not undermine any precondition of intelligibility; nor do we have biblical information that would be contrary to the idea that God may have created the matter in the universe very close to its present location. So, we should consider the possibility that galaxies currently in collision may have been created in collision. There is no reason to assume that they must have come from a previous state. The fact that it is possible to imagine a previous state which could have led up to the present state is logically irrelevant. After all, it is possible to imagine a previous state which would have led up to Adam’s adult state—namely a baby. Yet Adam did not come from such a state.
Starlight is different because we do have some Scriptural information about its origin. Namely, it really did come from the stars (Genesis 1:15). And our sensory experiences are basically reliable. Therefore events we see happening in space really have happened, which would seem to refute the light-in-transit model. Yet, starlight is not a challenge for a young universe when we consider the anisotropic synchrony convention. Taking all the Scriptural information into account, ASC seems to be implied by the Bible, and naturally solves the starlight problem by reducing inward-directed light-travel-time to zero. Moreover, ASC forms the basis for a new young-universe cosmological model which has made successful predictions.
References
Carson, D. A. 1984. Exegetical Fallacies. Grand Rapids, Michigan: Baker Book House.
Chaffey, T. and J. Lisle. 2008. Old-earth creationism on trial. Green Forest, Arkansas: Master Books.
Einstein, A. 1961. Relativity: The special and general Theory, authorized translation by R. W. Lawson. New York: Crown Publishers Inc.
Humphreys, D. R. 1994. A biblical basis for creationist cosmology. In Proceedings of the Third International Conference on Creationism, ed. R. E. Walsh, pp. 255–266. Pittsburgh, Pennsylvania: Creation Science Fellowship.
Kalas, P., J. Graham, E. Chiang, M. P. Fitzgerald, M. Clampin, E. S. Kite, K. Stapelfeldt, C. Marois, and J. Krist. 2008. Optical images of an exosolar planet 25 light years from earth. Science 322, no. 5906:1345–1348.
Lin, C. C. and F. H. Shu. 1964. On the spiral structure of disk galaxies, Astrophysical Journal 140:646–655.
Lisle, J. 2006. Taking back astronomy, pp. 48–50. Green Forest, Arkansas: Master Books.
Newton, R. 2001. Distant starlight and Genesis: Conventions of time measurement. TJ 15, no. 1:80–85
Salmon, W. C. 1977. The philosophical significance of the one-way speed of light. Noûs 11:253–292.
Sarkar, S, and J. Stachel. 1999. Did Malament prove the non-conventionality of simultaneity in the Special Theory of Relativity? Philosophy of Science 66:208–220.
Winnie, J. A. 1970a. Special Relativity without one-way velocity assumptions: Part I. Philosophy of Science 37:81–99.
Winnie, J. A. 1970b. Special Relativity without one-way velocity assumptions: Part II. Philosophy of Science 37:223–238.
















