Research conducted by Answers in Genesis staff scientists or sponsored by Answers in Genesis is funded solely by supporters’ donations.
Abstract
I examine the Dodwell hypothesis, that the earth underwent a catastrophic impact in 2345 BC that altered its axial tilt and then gradually recovered by about 1850. I identify problems with the selection and handling of certain ancient and medieval data. With the elimination of questionable data, a discrepancy may remain between ancient measurements of the earth’s tilt and our modern understanding of how the tilt has varied over time. This discrepancy, if real, does not demand the sort of catastrophe suggested by Dodwell, so there is doubt that this event occurred. If there were some abrupt change in the earth’s tilt in the past, the available data are not sufficient to fix the date of that event with any precision.
Keywords: catastrophism, obliquity of the ecliptic
Introduction
Nearly everyone is familiar with the earth’s axial tilt and knows that it is responsible for our seasons. A less well-known fact is that the direction and magnitude of the earth’s tilt slowly are changing due to gravitational forces of the sun, moon, and planets. These changes are well understood, but the late Australian astronomer George F. Dodwell (1879–1963) determined that ancient measurements of the earth’s tilt were at variance with that understanding. Fitting a curve to his data, Dodwell (Dodwell 1) concluded that the earth underwent a catastrophic change in its tilt in the year 2345 BC, and that the tilt had only recently recovered to the relatively stable situation now governed by the conventional theory. I understand that Dodwell was a Seventh Day Adventist, so he likely saw in this proposal a connection to biblical catastrophism. For instance, the 2345 BC date for the dramatic change in the earth’s axial tilt is very close to the Ussher chronology date of the Flood (2348 BC). Many recent creationists today think in terms of huge upheaval at the time of the Flood, including an impact (or impacts) related to the beginning of the Flood. Dodwell obviously was thinking in terms of an impact that altered the earth’s tilt. Some recent creationists today favor pushing the date of the Flood further back (the Septuagint chronology is nearly a millennium longer than the Masoretic text), and so in their thinking a 2345 BC impact would coincide with a post-Flood catastrophe. In this paper I will examine Dodwell’s hypothesis, but first, Syrus, we must define a few terms.
To better understand the terminology that I will use, I ought to start with the celestial sphere (fig. 1). Astronomers use the celestial sphere as a mental construct to describe the locations of objects and concepts of astronomical interest as seen from the earth. We imagine the earth to be a sphere at the center of the much larger celestial sphere (radius >> the earth’s radius) on which astronomical bodies and concepts are located. For instance, we can extend the earth’s rotation axis to the celestial sphere. The intersections of this axis and the celestial sphere are the north and south celestial poles. As viewed from either of the earth’s poles, the corresponding celestial pole would be directly overhead (the zenith). As the earth spins each day, astronomical bodies appear to revolve around the celestial poles. Since Polaris, or the North Star, is very close to the north celestial pole, it appears to stay relatively motionless as other stars, the sun, the moon, and the planets appear to revolve around it. As we can draw on the earth an equator half way between the poles, we likewise can construct the celestial equator half way between the celestial poles. The celestial equator will pass through the zenith at locations on the earth’s equator. Mathematically, the celestial equator is the great circle arc representing the intersection of a plane perpendicular to the axis of rotation.
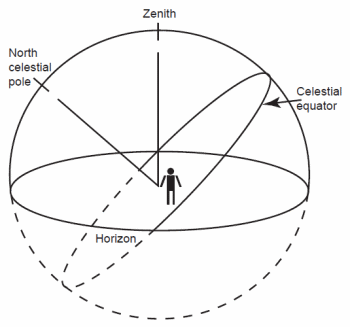
Fig. 1. The celestial sphere.
The earth’s revolution around the sun defines a plane as well (see fig. 2). The intersection of that plane with the celestial sphere is the ecliptic. Due to the earth’s orbit, the sun appears to move through the background stars on the celestial sphere along the ecliptic, taking one year to complete one circuit. The ecliptic is a circle, so perpendicular to the ecliptic is the axis around which the earth revolves each year. Where this revolution axis intersects the celestial sphere is the ecliptic pole. By definition, the angle between the earth’s rotation axis and revolution axis is the earth’s tilt. The angular separation of the north celestial pole and the ecliptic pole is the same angle, and the planes of the ecliptic and celestial equator have the same angular relationship. Since the earth’s tilt is a measure of how obliquely the ecliptic is inclined to the celestial equator, astronomers since ancient times have called this tilt the obliquity of the ecliptic, a convention that we shall follow here. We normally use ε to indicate the obliquity of the ecliptic.
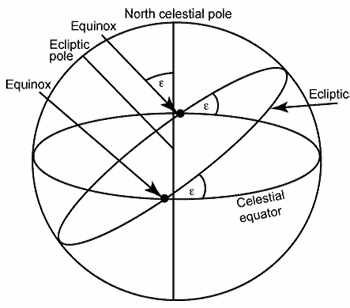
Fig. 2. The relationship between the ecliptic and the celestial equator.
The first measurements of the obliquity of the ecliptic are very ancient. For instance, Hipparchus, a second century BC Greek astronomer, determined that obliquity of the ecliptic was about 23°50´. Hipparchus also is credited with the discovery of the precession of the equinoxes, though this effect was not explained until after Newton developed physics. Precession is the gradual circular motion of the axis of a spinning object due to external torques (see fig. 3). The gravity of the sun and moon pulls on the equatorial bulge of the earth, attempting to reduce the earth’s tilt. If force were the only consideration, the pull of the sun and moon on the earth’s equatorial bulge would cause the obliquity of the ecliptic to go to zero degrees. However, the earth spins, so it possesses angular momentum. When a force acts on a spinning body in this way, the force produces a torque. The torque causes the direction of the rotation axis slowly to spin, or precess. In this case, the earth’s rotation axis precesses around the revolution axis, or we can say that the north celestial pole precesses around the ecliptic pole. It takes 25,900 years to complete one circuit. This causes the equinoxes, the intersections of the celestial equator and ecliptic, to slide gradually along the ecliptic, hence the name, precession of the equinoxes. During the precessional cycle the north celestial pole would move along a circle having angular radius equal to the obliquity of the ecliptic and centered on the ecliptic pole. Superimposed upon precession is nutation, a much smaller, similar effect of the moon with an 18.61 year period. Nutation is caused by the moon’s orbit being tilted to the ecliptic by about 5°—if the moon orbited in the ecliptic plane, then there would be no nutation. The magnitude of nutation is only 9.2′ of arc, far smaller than the nearly 23½° amplitude of precession. Both precession and nutation change the direction of the earth’s axis, but by themselves they don’t appreciably change the obliquity of the ecliptic, particularly on a timescale of only a few thousand years.
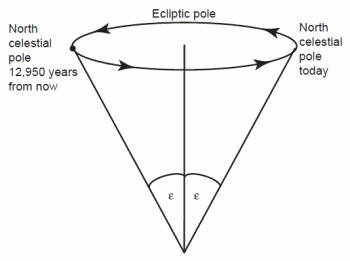
Fig. 3. The precession of the north celestial pole.
More complex interaction, particularly involving the planets will gradually change the obliquity of the ecliptic. If the moon were not present, the obliquity of the ecliptic would change over a very wide range, resulting in tilts from nearly 0° to 90°. Instead, the stabilizing effect of the moon limits the change in the obliquity of the ecliptic to about 2°. Wild swings in the obliquity of the ecliptic would have very devastating effects upon living organisms, so there is a design implication here. The current value of ε is 23.4°, and it has been decreasing for some time. In the secular view, a near maximum of 24.2° was achieved about 8500 BC. The physics affecting changes in the obliquity of the ecliptic is well known, and the theoretical value of ε is known with great precision far into the past and future. The value of the obliquity of the ecliptic is described by a polynomial function of time. For nearly a century the standard description of the obliquity of the ecliptic as a function of time was that of Simon Newcomb (1906, p. 237), determined about 1895. Newcomb’s formula is a third degree polynomial,1 but more recent treatments are fifth or even tenth degree. Dodwell used the Newcomb formula, because that was all that was available when Dodwell did his work. However, the high precision of much higher degree expressions is necessary only over very large time intervals. For the epochs of concern for the Dodwell hypothesis, there is no real difference between the Newcomb expression and others, so use of the Newcomb values is quite adequate.
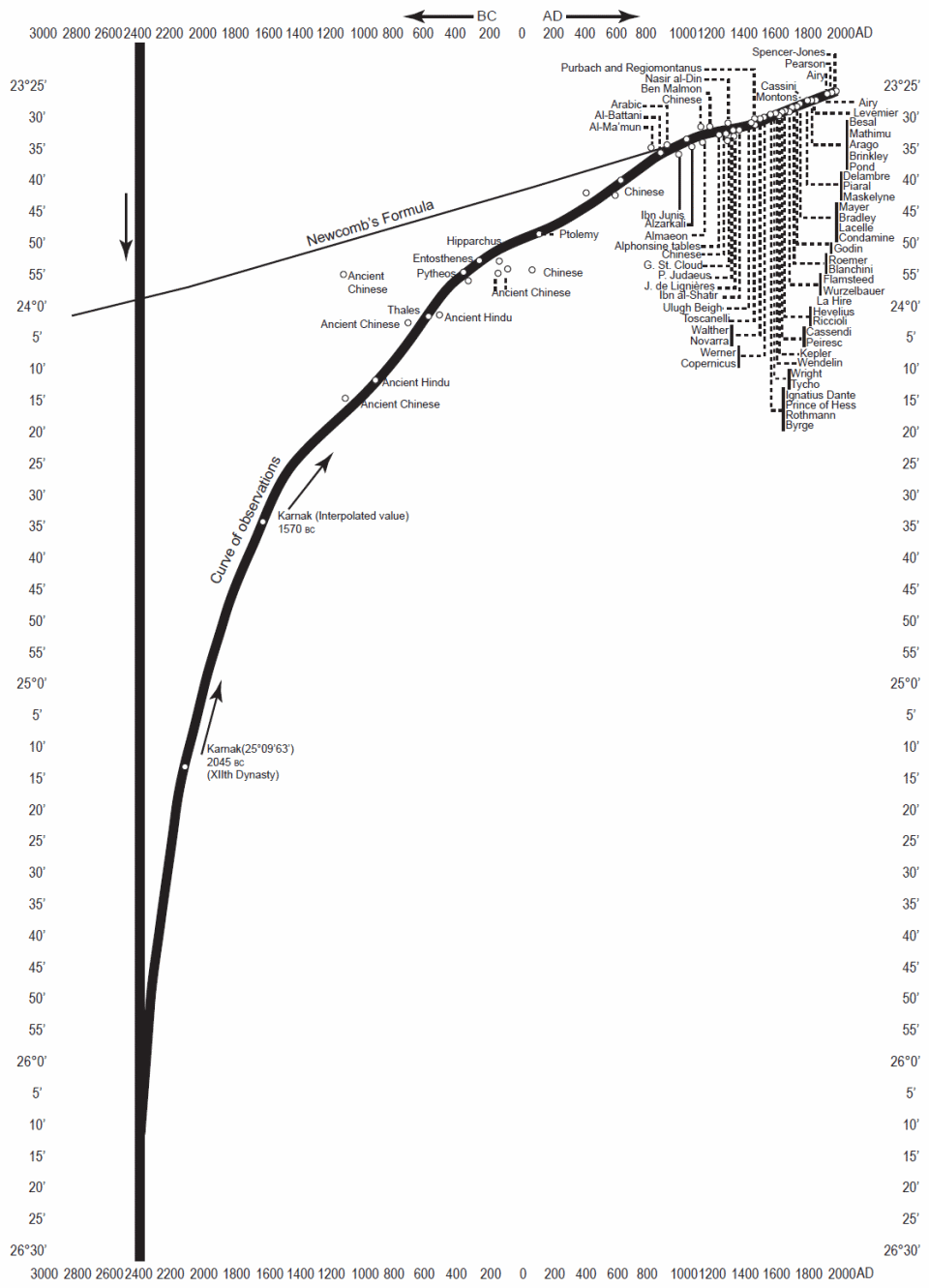
Fig. 4. Obliquity of ecliptic. Final curve. (Newcomb + log sin curve + oscillations) (from Dodwell).
Click image to view full size.
Dodwell saw a noticeable difference between the Newcomb formula and the values of obliquity of the ecliptic that he derived from historical measurements. Dodwell fitted a curve to his data, and in the curve he saw two trends superimposed upon the Newcomb curve. Fig. 4 shows Dodwell’s data and his curve fitted to the data (taken directly from the Dodwell manuscript). First, Dodwell’s curve primarily is a logarithmic sine curve that, going backward in time, increases without bound at the year 2345 BC. Dodwell thought that this represented a catastrophic event, perhaps an impact, at that date that drastically altered the obliquity of the ecliptic. Second, he saw superimposed upon the logarithmic sine curve a harmonic sine curve of diminishing amplitude that vanished about AD 1850. Dodwell thought that this was a curve of recovery from the catastrophic event. The possibility of such a catastrophic event obviously is of keen interest to recent creationists. This event, if real, could be identified with the Flood or, as some recent creationists believe, a possible post-Flood event.
I will analyze how credible this alleged event is. To do this, I will divide the problem into several parts. First, I will examine how well founded the data are. Second, where discrepancies between the data and the Newcomb formula exist, I will attempt to assess the likely errors in the data. Third, I will discuss whether the data with the appropriate error limits support either of the two trends that Dodwell noted.
Examination of the Data
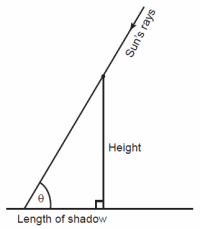
Fig. 5. The vertical gnomon.
The easiest and most direct way to measure the obliquity of the ecliptic is through the use of a vertical gnomon. A gnomon is a device used in casting the sun’s shadow for measurement purposes. The most common gnomon is on a sundial to cast a shadow on the scribed surface where the hour is read, but this gnomon normally is not mounted vertically. A vertical gnomon is a post of known height mounted perpendicular to a flat, level surface upon which the shadow of the sun is cast. The length of the shadow divided by the height of the post is the tangent of the altitude of the sun (Fig. 5). Altitude is the angle that an object makes with the horizon, which must be between 0° and 90°. Fig. 6 shows the situation of measuring the sun’s altitude at noon at the summer solstice and again at noon six months later at the winter solstice. At the summer solstice the sun will make an angle ε above the celestial equator, and at the winter solstice the sun will make an angle ε below the celestial equator, so that the difference of the altitude of the sun measured at noon on these two dates will be double the obliquity of the ecliptic. This apparently was the method used by Hipparchus, because Ptolemy (1952, p. 26) reported Hipparchus’ result as “more than 47°40´ but less than 47°45´.” One might expect to find the obliquity of the ecliptic by dividing this result by two, yielding 23°51.25´. However, there are three corrections to the observations that one must make. Those corrections are, in order of decreasing magnitude:
- Semi-diameter of the sun
- Refraction
- Solar parallax.
I shall now discuss each of these corrections.
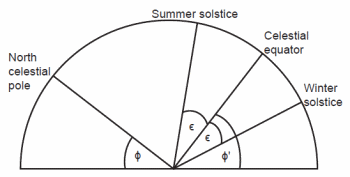
Fig. 6. The noon altitude of the sun at the summer and winter solstices.
The semi-diameter correction is necessary, because the sun is not a point source. See Fig. 7. Let point P be the bottom of the gnomon and point G be the top of the gnomon. The ray coming from the top of the sun will pass point G and fall at point A, while the ray from the bottom of the sun will fall at point B. Between points A and B there will be some sunlight, so only the penumbral shadow will be present there, but the full (umbral) shadow will extend from the bottom of the gnomon to point A. To do proper comparison of the sun’s altitude at different times, we need to know the altitude of the sun’s center, so it is important to know how to properly correct the observed shadow edge for the shadow that would be cast by rays coming from the center of the sun’s disk. The ray from the sun’s center will fall at point C, and so the altitude of the sun’s center will be angle GCP. The angle GAP is the observed altitude of the sun as determined by the length of the actual shadow. Let μ represent the half angular diameter of the sun. From geometry we see that the difference between the observed altitude and the altitude of the sun’s center is μ. Therefore we must correct the observed altitude of the sun by subtracting the half angular diameter of the sun. Because the earth has an elliptical orbit, the sun’s angular diameter is not constant, but varies between 31.6´ and 32.7´. Thus, the solar semi-diameter correction, μ, can be between 15.8´ and 16.35´. Since the range in μ is only 0.55´ and the likely error in measuring the altitude is at least 1´, in most cases it is acceptable to use the average, 16.08´. In this discussion I have assumed that a person observing the sun’s shadow would see it end at point A. However, the edge of the shadow will be a bit indistinct—will a person judge the shadow to end at point A, or at a point past point toward point C? Newton (1973, p. 367) previously has pointed out this problem, and decided that the error introduced by this ambiguity easily could account for 7–8 arc minutes or error.
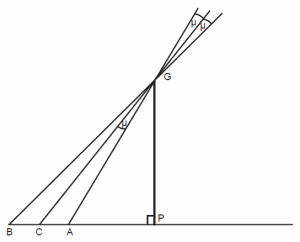
Fig. 7. The solar semi-diameter correction.
Dodwell described an experiment that he conducted in Adelaide, Australia, where several people measured the shadow of a gnomon that he constructed and compared the results to the accurately computed altitude of the sun’s center. He found that the average correction determined empirically was only 13.2´, a value that Dodwell apparently used in most of his data reductions. Dodwell neither acknowledged nor commented as to why this correction was nearly 3´ less than expected. Much of this probably is due to the indefinite edge of the sun’s shadow mentioned above. Dodwell reported that his results came from a total of 172 measurements made by 9 individuals, and he further reported the range of the highest (15.3´) and lowest (10.4´) measurements from the average, and he compared the mean of those two to the overall mean. However, without more information it is not possible to compute the standard deviation or probable error. From this limited information the likely error of measurement was at least 1´ and probably more. It might be profitable to repeat this experiment to properly ascertain the error of observation.
If one determines the obliquity of the ecliptic by the above described method in the temperate zone, the correction for the sun’s semi-diameter is made in the same sense for both measurements, so the effect cancels out. Therefore the exact value of the correction is not important. On the other hand, the earth currently comes to perihelion less than two weeks after the winter solstice and to aphelion less than two weeks after summer solstice, so if a variable correction is applied, the correction at winter solstice is greater by about a half minute of arc. Dodwell did not discuss whether he considered this correction in his computations.
The correction for refraction is necessary, because the earth’s atmosphere bends, or refracts, light as it passes through. This phenomenon is well understood, and it is easy to compute using the plane-parallel approximation, if the altitude is not too low. All the data considered by Dodwell met this criterion. Refraction causes light to bend downward, making the altitude appear greater than it actually is, so we must subtract this correction to get the true altitude. Let ζ be the zenith distance, the angle that the sun makes with the zenith. Since the zenith is directly overhead, ζ is the compliment of the altitude. The correction is given by ρ = 58.2” tan(ζ) (Smart 1977, p. 26). The correction is much greater at the winter solstice so that the corrections for summer and winter can differ by more than an arc minute. This is the correction with the greatest effect for measurements made in temperature latitudes.
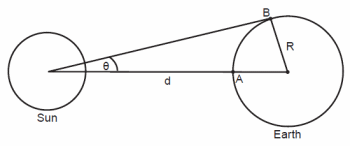
Fig. 8. Solar parallax.
The correction for solar parallax is necessary, because the sun’s distance is not infinite, and so people observing the sun at different altitudes are not looking in parallel directions. For proper comparison, we adjust altitude measurements to what they would be if the sun’s rays traveled along paths parallel to the line connecting the center of the sun to the center of the earth. Consider two observers located at points A and B on the earth looking at the sun (fig. 8).2 Point A is along the subsolar line and so requires no correction, but point B is as far off the subsolar line as possible, requiring the maximum correction. Using the small angle approximation, the maximum angular displacement for these two observers is θ = R/d, where R is the earth’s radius and d is the distance to the sun. This angle is about 8.8”. Point B corresponds to viewing the sun on the horizon. Since the altitude measurements considered here were taken at noon not in the arctic, the correction for solar parallax always will be less than the maximum of 8.8”.
Consider an observer at point C located at a distance x above the subsolar line (fig. 9). Let δ be the angle that the line between point C and the earth’s center makes will the subsolar line. The solar parallax correction will be ψ. Now, x = R sin δ, and by the small angle approximation,
ψ = x/d = (R/d) sin δ = 8.8” sin δ.
Since all observations of interest here are made at noon on the solstices, δ is a simple function of ε and the latitude of the observations, so the solar parallax correction is easy to compute. This correction will be less than the maximum of 8.8”, and so the correction is at least an order of magnitude less than the error of observation. Given that this correction is dwarfed by the other two, one may question the necessity of applying it. The only possible gains in applying it are to be as thorough as possible and to avoid round-off errors that could propagate through. In checking the work of Dodwell I made all three corrections, and in many cases I was able to accurately reproduce his results. A few I was not able to replicate exactly, but the differences between my computations and those of Dodwell were less than the likely errors in the original measurements.
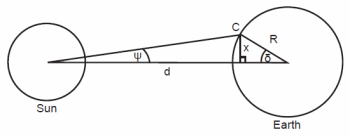
Fig. 9. The correction for solar parallax.
Let us now consider some specific measurements that Dodwell discussed. Pytheas, a contemporary of Alexander the Great, was famous for an extensive voyage. He measured the altitude of the noon sun on the summer solstice where he lived in Massalia, a Greek colony at the site of modern Marseilles, France. We assume that the date was about 325 BC, and we know the location of the city, but there is a discrepancy in the reporting of his measurement. Dodwell (Dodwell 1) wrote that Strabo said that the height of the gnomon to the length of its shadow was 120:41⅘,3 while Ptolemy said that the ratio was 60: 20⅚ = 120: 41⅔. The corresponding values for the observed solar altitude are θ = 70°47´42” and θ = 70°51´7”. Note that these values differ by only 3´25”. The situation is diagrammed in Fig. 10. The altitude of the north celestial pole is equal to the latitude, φ. Since the celestial equator is at right angles to the north celestial pole, the altitude of the celestial equator is the compliment of the latitude, φ´. At the summer solstice the sun is at an angle ε above the celestial equator, so the altitude of the sun,
θ = ε + φ´ = ε + 90°−φ.
Or,
ε = θ + φ−90°.
Dodwell (Dodwell 7) took the latitude of Massilia to be 43°17´52”, the latitude of the old Marseilles observatory near the port. This appears to be very close to the latitude where Pytheas made his measurement. We can apply the three corrections to get two values for the obliquity of the ecliptic, one each for the measurements reported by Strabo and Ptolemy. Dodwell (Dodwell table) reported values of ε to be 23°53´46” and 23°54´53”, but I have not been able to reproduce these values, for I got 23°52´5” and 23°55´29”. There is something strange here, for this amounts to a single observation made at one place and time, so the sun’s semi-diameter and solar parallax corrections are the same. The two slightly different altitudes reported result in a difference in the refraction correction of far less than an arc second. Therefore from the above equation it is obvious that two computations of ε turn out to differ by 3´25”. My two values differ by this amount (with a one second round-off error), but Dodwell’s values differ by only a third of that amount.
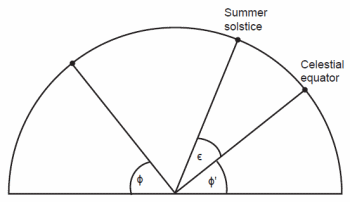
Fig. 10. The measurement of Pytheas.
This probably is a good time to point out that, while we can compute the obliquity of the ecliptic to the nearest arc second, the error of observation likely is at least a minute of arc, so reporting measurements of the obliquity of the ecliptic to the nearest arc second (as Dodwell did) is meaningless. For comparison and to avoid round-off error, it is good practice is to compute ε to full accuracy but then settle upon final values to the nearest arc minute at best. Following that procedure, Dodwell’s values round to 23°54´ and 23°55´ and mine round to 23°52´ and 23°55´. Furthermore, following the conventional rule of averaging half values to the nearest even digit, either of our two values average to the same 23°54´. If we recognize that the errors of observation may result in an error of plus or minus three arc minutes, then all four of these values are within that range. That is, while I cannot exactly replicate Dodwell’s results here, his values are well within the accuracy probably allowed.
Dodwell applied similar methodology to Ptolemy’s aforementioned statement based upon observing the altitude of the sun at the two solstices that the obliquity of the ecliptic was “always more than 47°40´ but less than 47°45´”.4 By knowing the latitude of Alexandria, Egypt where Ptolemy did his work, Dodwell was able to determine what Ptolemy’s measured altitudes were. Note that Ptolemy did not report these altitudes, but that Dodwell inferred them from the result. Let α be the observed altitude of the sun at the winter solstice and β be the observed altitude of the sun at the summer solstice. Let μ be the correction for the sun’s semi-diameter, ρ be the correction for refraction, and ψ be the correction for solar parallax. If θ1 is the corrected altitude of the sun’s center on the winter solstice and θ2 is the corrected altitude of the sun’s center on the summer solstice, then those values are determined by
θ1 = α1−μ1−ρ1 + ψ1
and
θ2 = α2−μ2−ρ2 + ψ2,
where the subscripts 1 and 2 refer to the corrections made at the winter and summer solstices, respectively. Note the corrections in the sun’s semi-diameter and refraction decrease the true altitude, but that the correction for solar parallax increases the angle. From Fig. 6 you can see that
θ1 = φ´−ε = 90º−φ−ε
and
θ2 = φ´−ε = 90º−φ−ε.
Combining these four equations, we find
ε = ½ [(β−α)−(μ2−μ1)−(ρ2−ρ1) + (ψ2−ψ1)].
In this expression (β − α) is the observed difference in the altitude of the sun measured at noon during the summer and at the winter solstice, the amount fixed by Ptolemy to be between 47º40´ and 47º45´. This observational error of 2.5´ in (β − α) would appear to dominate over the errors of the other terms in the expression. When Dodwell applied these corrections, he determined ε to be 23º52´4”, a value that I replicated within two arc seconds. Rounding to the nearest minute of arc, the value of ε is 23º52´, but with a likely range of 23º50´ − 23º54´. With full consideration of error in the other terms and rounding, one could argue that the range ought to be 23º49´ − 23º55´.
While I agree with Dodwell’s computation of the obliquity of the ecliptic based upon this ancient measurement, Dodwell assigned this measurement to the wrong epoch, at the time of Eratosthenes, more than 350 years before Ptolemy. This is based upon a misunderstanding of The Almagest. Dodwell wrote:
Ptolemy tells us that the double obliquity angle observed by Eratosthenes and Hipparchus was less than 47º45´ (maximum value) and greater than 47º40´ (minimum value). (Dodwell 5)
Here is the relevant passage from The Almagest:
… we found the arc from the northernmost to the southernmost limit, which is the arc between the tropic points, to be always more than 47º40´ but less than 47º45´. And with this there results nearly the same ratio as that of Eratosthenes and as that which Hipparchus used. For the arc between the tropics turns out to be very nearly 11 out of the meridian’s 83 parts. (Ptolemy 1952, p. 26)
Ptolemy clearly stated that “we found” this value, apparently referring to himself and his colleagues in Alexandria. He then goes on to note that this value of twice the obliquity of the ecliptic agrees with the earlier measurements of Eratosthenes and Hipparchus.
Newcomb’s value for the obliquity of the ecliptic at the epoch of Ptolemy is 23º40´41”. This is only two seconds off from the value of 23º40´39” from Laskar (1986, p. 59), a tenth degree polynomial expression, showing that at the epochs of concern it doesn’t matter which standard formula of the obliquity of the ecliptic that we use. The measurement of Ptolemy is about ten arc minutes greater than that expected from Newcomb and well outside of the range suggested by Ptolemy.
Dodwell (Dodwell 5) computed a measurement of the obliquity of the ecliptic supposedly using data from Ptolemy. For this Dodwell relied upon the work of a 17th century Flemish astronomer, Godefroy Wendelin,5 but since Dodwell didn’t reference either Wendelin’s statements or where the data supposedly came from Ptolemy, this is difficult to verify. It appears that Wendelin noted that Ptolemy had observed the moon just 2⅛° from the zenith when the moon was at the summer solstice at its maximum distance north of the ecliptic. There is something garbled here, because the sentence as constructed indicates that Ptolemy recorded “numerous observations” of this, but this isn’t possible, since this circumstance happens, at best, once every 19 years. Dodwell converted 2⅛° to 2º7´30”, corrected for refraction and lunar parallax, and, knowing the ecliptic latitude of the moon at that point and the latitude of Alexandria, determined that the obliquity of the ecliptic was 23º48´24”. Dodwell also computed that this (rare) event must have happened in AD 126. However, in his tabulation of all data used in his study, Ptolemy’s single point is listed as 8” less and in the year AD 139. This discrepancy is insignificantly small, but unexplained. And it is outside of the range for the obliquity of the ecliptic previously determined from a more direct measurement of the obliquity of the ecliptic derived from Ptolemy’s work.
This datum is fraught with problems. It is a very indirect method, relying upon data not collected for the purpose of determining the obliquity of the ecliptic. It is not well documented, making it impossible to verify, and it is not consistently reported in Dodwell’s report. Furthermore, the error involved may be larger than most. The zenith distance of the moon was reported as 2⅛°. What does this mean? In the modern manner of reporting data, it would seem that the error of measurement is ± 1⁄16° = 3´45”. Whatever the error, it would propagate through to the final result, so the final value of ε could be between 23º45´ and 23º52´, rounding off to the nearest minute of arc. The range of this datum overlaps the range of the earlier determined Ptolemaic obliquity of the ecliptic. Given the problems with this one point and the fact that what appears to be a more reliable determination of ε that is consistent with this datum with some reasonable error analysis, it is best to omit this datum from further consideration.
Dodwell again relied upon Wendelin to determine the value of the obliquity ostensibly at the time of Hipparchus, a very important second century BC Greek astronomer credited with the discovery of the precession of the equinoxes. Dodwell quoted Wendelin,
… from his own observations stated the distance between the topics was in proportion to the whole circle as 11 is to 83, exactly the same as Eratosthenes, and found the maximum obliquity 23º51´20”. (Dodwell 5)
The source of this information obviously is from The Almagest (quoted above), where Ptolemy stated that his determination of twice the obliquity of the ecliptic was the same as that of Hipparchus and Eratosthenes. In fact, Ptolemy’s statement appears to attribute the 11 to 83 ratio to Eratosthenes, not Hipparchus as Wendelin seemed to think. Nor is the method of the determination mentioned, though Dodwell assumed that it was done with a vertical gnomon. Dodwell applied corrections assuming that this was the method used and at the location of Rhodes where Hipparchus lived, though use of the correct location of Eratosthenes at Alexandria is unlikely to change the result much. With his correction Dodwell computed the obliquity of the ecliptic to be 23º52´16”, about a minute of arc greater than determined by Wendelin. Wendelin almost certainly didn’t correct for refraction, which is on the order of the difference. Rounding to the nearest minute, we get 23º52´, the same result discussed above from Ptolemy, but this is no surprise since Ptolemy stated that his value agreed with that of Eratosthenes and Hipparchus.
What is the meaning of Ptolemy’s statement that the obliquity of the ecliptic was “very nearly 11 out of the meridian’s 83 parts?” Does this mean that the first number was 11 plus or minus a small amount or that the number was a little less than 11? Or does it mean that the ratio was 11 to the number 83 more or less? The latter interpretation is the most conservative, and it allows us to estimate some error. Interpreting this as the higher number in the ratio is closer to 83 than it is to 82 or 84, I find a plus or minus error of 8´ in the 23º52´ measurement of the obliquity of the ecliptic. This error perhaps is too great, but applying this error gives the minimum value of the obliquity of the ecliptic of 23º44´, a minute of arc greater than the Newcomb value of 23º43´13” at the epoch of Eratosthenes. Of course, with one of the alternate interpretations mentioned above, the error is greater, and the result then is consistent with Newcomb.
Dodwell computed four measurements of the obliquity of the ecliptic from Eratosthenes’s data, making several assumptions and conjectures about what Eratosthenes did at both Alexandria and Syene (modern day Aswan, Egypt). For instance, Dodwell seemed to think that the legendary well at Syene with no shadow on its bottom at noon on the summer solstice and thus supposedly inspired Eratosthenes to measure the size of the earth was exactly on the Tropic of Cancer at the time of Eratosthenes. However, this is not necessarily true, and there are several reasons to doubt this. First, the story may be apocryphal. Second, one must assume that the walls of the well were vertical on all sides. Third, the semi-diameter correction produces a “gray” region in latitude where one might see no shadow, but Dodwell assumed that this location was exactly on the edge of this region. Dodwell’s four computations round to 23º52´, and none of the four differ from this round number by more than 13”. Since this agrees with the aforementioned measurement of the obliquity of the ecliptic from the 11:83 ratio, there is no reason to treat these as additional data.
Dodwell again relied upon Wendelin to determine the obliquity of the ecliptic at the time of Thales, a sixth century BC Greek philosopher from Miletus (on the western coast of modern day Turkey). Dodwell quoted Wendelin as writing that Thales
… defined the interval between the two tropics as 8 parts out of 60 of the whole circle. From this we find the interval 48º, as we divide the circle into 360º, so that the maximum obliquity of the sun was 24 whole degrees. (Dodwell 5)
Dodwell took this measurement of the obliquity of the ecliptic to be exactly 24º, assumed that it came from vertical gnomon observations, and corrected for the location of Miletus to yield a final result of 24º0´56” that easily rounds to 24º1´. But was the ratio exactly 8:60? Not likely. Again, taking a conservative approach and treating the measures as we would today, there is a plus or minus error of 12´. That is, this measure of the obliquity of the ecliptic could be as low as 23º49´ and as high as 24º13´. The Newcomb value for the obliquity of the ecliptic at the epoch of Thales is 23º45´50”, three minutes less than the minimum value considered here.
This idea that the obliquity of the ecliptic was in ratio of 1:15 was prevalent in many ancient cultures. This is a nice round ratio, but unfortunately Dodwell often treated this as a precise statement, erroneously concluding that the value was 24º0´0”. For instance, Dodwell presented a measurement of the obliquity of the ecliptic from India (Dodwell 4) contemporary to Thales and similarly expressed as the one attributed to Thales. He referenced Brennand (1896) in saying that the ancient Indians thought that the obliquity of the ecliptic at that time was 24º0´. Assuming the location of observation and the use of a vertical gnomon, Dodwell corrected this to 24º0´44”. Dodwell assumed a very precise measurement of 24º0´, but Brennand did not claim this precision. The two pages Dodwell referenced (Brennand 1896, pp. 80, 236) say that the obliquity of the ecliptic was “24º.” And elsewhere Brennand (1896, p. 47) said that the obliquity of the ecliptic was “nearly 24º.” Brennand never stated that ε was 24°0´, so Dodwell claimed far more precision here than is warranted, so this datum is deleted from further discussion. Dodwell presented an Indian determination of the obliquity of the ecliptic from an even earlier epoch, but it was based upon what appears to be a cosmological model. Dodwell computed from the specifics of the model precisely what the obliquity of the ecliptic would be, made corrections, assuming the latitude of observation, and found 24º11´4” for the obliquity of the ecliptic. However, there are many questions here, such as whether the description of the cosmology was intended to accurately convey what the Indians of the time thought that the obliquity of the ecliptic was. Given the uncertainties, it is best to view this measurement with caution.
Dodwell included a chapter on ancient Chinese measurements of the obliquity of the ecliptic (Dodwell 3), but these are impossible to evaluate, because he offered none of the original data. And by his own account, the data were transmitted several times, passing from an early 18th century French missionary in China to a French astronomer at that time, and later to the famous Pierre-Simon Laplace. As we saw with Wendelin’s handling of quotes of Ptolemy, such transmission can alter meanings. With these reservations, I am skeptical of the ancient Chinese measurements of the obliquity tabulated by Dodwell, and so I will not consider them further.
Dodwell tabulated many medieval measurements of the obliquity of the ecliptic. In the medieval period the difference between Dodwell’s curve and Newcomb’s curve are smaller than during ancient times. Dodwell acknowledged that most of the medieval measurements of the obliquity did not include discussions of corrections, if any, which were made. He assumed that many of them made the correction for the sun’s semi-diameter, but that they used the much too high Ptolemaic solar semidiameter, so Dodwell re-computed the obliquity of the ecliptic by first removing the incorrect semi-diameter and then adding the correct one. What was the reason for this? Dodwell found that many of the medieval measurements of the obliquity of the ecliptic agreed with the Newcomb formula, but not with his curve. He even re-computed some measurements on the assumption that some of the gnomon used may have had a conical top, requiring an additional correction. Why? In his own words at the conclusion of his chapter 6, Dodwell wrote,
If we admit that some of the Arab observations were corrected for Ptolemaic parallax, and some were not, and also that, probably in the earliest part of the period, a gnomon with a conical top may sometimes have been used, then the observed mean value of the Obliquity would agree more closely with the new Curve than with Newcomb’s Formula. (Dodwell 6)
That is, Dodwell altered some of the medieval data to better fit his thesis. Which points did Dodwell not correct for the incorrect Ptolemaic solar semi-diameter? The ones that fit his thesis without this correction. At the end of his sixth chapter Dodwell plotted raw and corrected measurements of the obliquity of the ecliptic as a function of time, along with curves representing his thesis (with and without the oscillation) and Newcomb’s formula. The corrected data scatter around Dodwell’s curves, but the raw data match the Newcomb formula pretty well. One could easily argue that the medieval measurements do not support the Dodwell hypothesis. The medieval data support the Dodwell hypothesis only with manipulated data. This is begging the question. Given this, and the fact that the supposed discrepancies are so small during this period, it is best to eliminate the medieval data from discussion.
Dodwell included some more recent measurements of the obliquity of the ecliptic. For instance, at the end of his seventh chapter there is a table containing 42 measurements from 1660 to 1868, along with the discrepancies from the Newcomb curve. The largest discrepancy is −16”, and the discrepancies sum to −1”. The standard deviation is 5.5”. These modern values are of no help in discriminating between the Newcomb curve and the Dodwell hypothesis.
Probably the most important datum in support of the Dodwell hypothesis is the alignment of Temple of Amun Re in the Karnak Temple Complex in Egypt. Its importance stems from its antiquity, with Dodwell’s adopted date of construction of 2045 BC, when the difference between the curves of Newcomb and Dodwell is much greater than at later epochs. Sir Norman Lockyer (1894) was one of the first to suggest that ancient Egyptian temples had alignments with the rising and setting of various astronomical bodies. Drawing from Lockyer, Dodwell discussed alleged alignments of the solar temples at Heliopolis and Abu Simbel. The former would have had alignment with the setting sun on two specific dates, and the latter with the direction of the rising sun on two other dates. None of these dates are the solstices or equinoxes. In 1891 Lockyer took note that the alignment at Karnak was close to the azimuth of the setting sun on the summer equinox. Supposing that this was the purpose of the alignment, Lockyer asked that the site be surveyed and even checked empirically on the summer solstice. When this eventually was done, it proved not to be viable, even when corrected for Newcomb’s obliquity of the ecliptic. Of course, if the Newcomb curve is in error, as Dodwell argued, then the alignment may have occurred at the time of construction. Conversely, because of the antiquity of this structure, this alleged alignment became an important datum in establishing the nature of the Dodwell curve. This is demonstrated by the fact that the obliquity of the ecliptic derived from this assumption lies precisely on the Dodwell curve, as well as a later (1570 BC) point also from Karnak. If these two points are removed, any number of very different curves could be fitted to the remaining Dodwell data.
Dodwell made his case for various solar alignments by quoting sources on ancient Egyptian rituals and construction. One must be careful in evaluating these, because while some appear to be translations of inscriptions, many are conjecture of the authors. The translations of the inscriptions quoted refer to the king looking to the stars while laying the foundation of a temple, but no solar alignment is mentioned. Apparently, no such inscriptions exist at Karnak, because these translations come from elsewhere. But read what Dodwell concluded about Karnak:
From what has now been said about the orientation ceremonies, so carefully carried out by the Egyptian temple-builders, we have good reason for believing that the Temple of Amen Ra at Karnak, the most important solar temple in Egypt, was truly oriented to the setting sun at the summer solstice in the year of its foundation, about 2045 BC. (Dodwell 8)
The quotes about the ceremonies that Dodwell offered preceding his statement here said nothing about solar alignment, so this is conjecture about Karnak. A bit later Dodwell quoted from a translation of an inscription about the worship ceremony at Heliopolis, though that narrative contains no mention of sunlight flooding down a passage at a particular moment. Dodwell follows the quote with this observation:
This inscription relates to a ceremony which took place at Heliopolis, but it is obviously the typical service of the Egyptian solar temple; a similar procedure would be followed at the Karnak temple, and the Egyptians at Thebes doubtless took advantage of this impressive spectacle in the ritual for the Temple of Amen Ra. (Dodwell 8)
Dodwell has embellished what we actually know of the temple ceremony at Heliopolis, and then transferred it to Karnak. In short, the only evidence that the alignment was to view sunset on the summer solstice is that the azimuth of the passage is approximately correct for doing so, but it is conjecture to say that this is of necessity the case.
Egyptologists have been very unreceptive to most of the alleged astronomical alignments of ancient Egyptian temples. They likely would be convinced if there were inscriptions that actually showed this to be the case, but apparently no such inscriptions exist. A recent survey of the orientation of ancient temples in Upper Egypt and Lower Nubia (Shaltout and Belmonte, 2005, p. 273) is most interesting. This survey listed the azimuths of axes of symmetry in nearly every temple in the region, including all of those at Karnak. There are more than 100 entries. They also listed the declinations of astronomical bodies that would be visible at rising or setting along the axes of symmetry. There is a strong cluster of these at declination = −24º, which was the position of the sun at the winter solstice at the time. Furthermore, there is a preponderance of axes oriented toward the southeast (azimuth 115º−120º, depending upon latitude), indicating some interest in aligning with sunrise in ancient Egypt, but no evidence of interest in sunset at any solstice. The authors noted that “curiously enough, the other solstice, the summer one at 24º is basically absent from our data.” Indeed, the only one that I saw in the table that was close to this was the 25.4º azimuth of the Amun Re. If this truly was to align with the setting sun on the summer solstice as Dodwell (and Lockyer before him) concluded, then it makes this temple unique, at least in Upper Egypt and Lower Nubia. Furthermore, if this axis aligned with the sun when the obliquity of the ecliptic was much larger than that according to the Newcomb curve, then one must explain all the other alignments of the rising sun at winter solstice according to Newcomb but would not have aligned if Dodwell is right. Preponderance of the data argues against the alignment of Karnak being solsticial.
If Dodwell is wrong, then what is the significance of the azimuth of the axis at Amun Re? The authors of the temple study have an excellent suggestion. They also tabulated the angle that the axes of symmetry made to the direction of the flow of the Nile River at each location. Most axes, including the one in question here, are aligned at right angles to the river. This suggests that once a site for a temple was selected, the axis was laid out so that one viewed the axis of symmetry as one approached the temple from a boat on the river. This makes sense, because most sites probably had boat landings at their entrances, and so this would have grand entrances for nearly everyone who visited the sites.
Dodwell discussed Stonehenge in his chapter 9 (Dodwell 9). Because the architects of Stonehenge left no records, we don’t know its purpose. There are a number of possible astronomical alignments, so theories abound. Of particular interest is the Avenue, which aligns well with sunrise on the summer solstice. If this and other alignments truly have astronomical significance, then it is possible to determine the obliquity of the ecliptic at the time of construction. Indeed, determining the date of construction was one of the purposes in measuring the azimuths of such alignments. In the 19th and well into the 20th century many people thought that Stonehenge was constructed by the Druids, which would date it to the first millennium BC. This was the thinking during Dodwell’s lifetime, for he commented:
We see, from the results, that the astronomical date, found by using either Stockwell’s or Newcomb’s formula, is greatly out of agreement with the modern archaeological investigation previously described.When the formula is corrected, however, by means of the New Curve of Obliquity, in the same was as for the oriented Solar Temple of Karnak, the astronomical date agrees with archaeology and history. (Dodwell 9)
John N. Stockwell was an astronomer who had written on the time dependence of the obliquity of the ecliptic prior to Simon Newcomb. Newcomb’s formula improved upon Stockwell’s treatment. Using archaeological conclusions then available, Dodwell rightly noted that the date of construction of Stonehenge did not conform to the obliquity of the ecliptic from Newcomb’s formula but agreed well with his determination of the obliquity of the ecliptic at the epoch of Stonehenge’s construction. However, in the past half century much archaeological work has been done at Stonehenge. According to his preface, Dodwell did much of his work in the 1930s. Since that time archaeologists have revised the time line of Stonehenge, placing its construction over several stages, but all much earlier than the Druids in England.6 The date today for the Avenue is at the same epoch derived from the Newcomb value of the obliquity of the ecliptic. Curiously, while Dodwell had derived obliquity of the equinox measurements at various dates from many historical observations and several other archaeological sites, he did not do so for Stonehenge, for he neither tabulated nor plotted a datum from Stonehenge. This may be because of uncertainty in precisely dating the construction of Stonehenge in his time. Rather, he used what was then thought about the age of Stonehenge as a sort of test for his hypothesis. That is, what was then believed about Stonehenge contradicted the Newcomb theory but matched Dodwell’s prediction. However, since then the understanding of Stonehenge has radically changed, and the modern dating of Stonehenge matches Newcomb’s curve, but not Dodwell’s. In this sense Dodwell’s theory fails the very test that he proposed.
Analysis
Dodwell presented a lengthy table of historical measurements of the obliquity of the ecliptic that he had determined (Dodwell table), and he plotted those as a function of time in his Fig. 6, along with a plot of Newcomb’s formula. There is an obvious departure between the data and Newcomb’s curve. Dodwell also plotted in the figure a log sine curve that he fitted to the data. The agreement between the data and his curve is good, though this is not surprising, since he fitted the curve to the data. The best fit is at the earliest epochs and at the latest epochs. The fit at the latest epochs is not surprising, because those data are the most numerous and the most accurate and thus have little scatter. The fit at the earliest epochs isn’t surprising either, because the only two points there show the most radical departure from what is expected from Newcomb, and they represent nearly one quarter of the entire time interval concerned. By mathematical necessity the curve fitted to the data must pass through or very closely to those two points, so the excellent fit there is not surprising. The greatest scatter in the data is in between, in the first millennium BC and very late second millennium BC. Thus the scatter here probably gives us an idea of the likely errors of the ancient measurements of the obliquity of the ecliptic. Judging by the curve, those errors appear to be a few arc minutes.
In his Fig. 4, Dodwell plotted his data fitted to his log sine curve. Dodwell saw in that plot an oscillation of diminishing amplitude with a period of 1,198 years. He judged that the oscillation had gone through 3½ periods before subsiding about 1850. Dodwell included the plot of this oscillation in his Fig. 4. From that plot the maximum amplitude of the alleged oscillation is less than 3´. By 200 BC where the amplitude is less than 2´ there is much scatter in the data, with the residual of some data points exceeding the amplitude. Dodwell did not compute statistics of this harmonic term, but because of the large scatter in the data compared to the alleged amplitude of the oscillation, it appears to be a poor fit to the data. If error bars of a few arc minutes were displayed on the figure, the need for a harmonic term would vanish.
If we were to apply those same errors to the first two data points (those of Karnak, 2045 BC and 1570 BC), any number of curves could pass through the data. If we were to stick with a log sine curve, the point of verticality at 2345 BC would shift. Thus, with inclusion of likely errors the precision of Dodwell’s date of 2345 BC of the catastrophic event is not supportable. Note that this does not preclude that such an event took place, but only that we could not establish the date of the event with such certainty.
But what if the axis of symmetry at Karnak was not aligned with sunset on the summer solstice, which is by far the majority (unanimous?) opinion of Egyptologists? Those two points drive Dodwell’s thesis to the extent that their elimination would seriously undermine Dodwell’s work. A linear expression but with a different slope than Newcomb’s probably could fit the remaining data well. Non-linear expressions would fit too, though nothing nearly as drastic as Dodwell’s catastrophic change in the obliquity would be required. Therefore, the elimination of the earliest, very questionable data strongly argues against the Dodwell hypothesis.
Does this mean that the Newcomb formula must be correct? Not necessarily. In the previous section I criticized Dodwell’s unwarranted precision of many of the measurements of the obliquity of the ecliptic. I also argued against inclusion of questionable data. What data would I exclude and what would I include? Modern measurements (last four centuries or more) differ so little from Newcomb’s curve as to be irrelevant in this discussion. The medieval measurements listed by Dodwell deviate from Newcomb’s curve more than modern ones, but many of them would be consistent with Newcomb if appropriate errors were considered. Furthermore, as I previously described, Dodwell massaged some of the medieval data by removing alleged incorrect solar semi-diameter corrections of data that agreed better with the Newcomb curve than with his curve. These considerations warrant removal of the medieval measurements. I reject the two data from Karnak, because Egyptologists reject the conclusion upon which they are based. I also reject the ancient Chinese and Indian measurements, because I lack information to further check them. This leaves the measurements gleaned from the work of Thales, Pytheas, Eratosthenes, and Ptolemy, and I would change the epoch of at least one datum from that of Dodwell. Furthermore, I would eliminate some of the duplication that Dodwell had, such as the four measurements taken from Eratosthenes. This amounted to over-mining of the information. Besides, all four are well within the likely errors of the observation. This pares the data far from Dodwell’s total number to four points. These four measurements of the obliquity of the ecliptic are in Table 1, along with the epoch and errors that I assessed in the previous section. Supporters of Dodwell may cry foul over my paring of the data, but a plot of these points proves most interesting.
Table 1.
| Name | Epoch | ε | Error |
|---|---|---|---|
| Thales | 558 BC | 24º 01´ | 12´ |
| Pytheas | 326 BC | 23º 54´ | 3´ |
| Eratosthenes | 230 BC | 23º 52´ | 8´ |
| Ptolemy | 139 AD | 23º 52´ | 3´ |
The data are plotted in Fig. 11, along with a plot of Newcomb’s formula for the obliquity of the ecliptic. With the points I have included error bars reflecting my assessed errors. Note that the direction of increasing obliquity of the ecliptic is downward, following the convention of Dodwell’s plots. Not only do all data points, sparse as they are, fall below the Newcomb curve, so do all the error bars of the points. If these data are to be believed, they strongly suggest a noticeable departure from the Newcomb formula approximately 2,000 years ago. If true, then there is a major factor affecting the obliquity of the ecliptic (at least in the past, if not effective today) that the Newcomb and other similar definitive treatments fail to account for. However, I may have underestimated the errors. If Newton’s analysis is correct, then the Newcomb curve falls within the error bars of these data and there is no discrepancy. If Newton overestimated the errors, then there is a modest discrepancy between Newcomb and the observations, but this does not necessarily lead us to the Dodwell hypothesis for a single catastrophic event or for a decaying harmonic term.
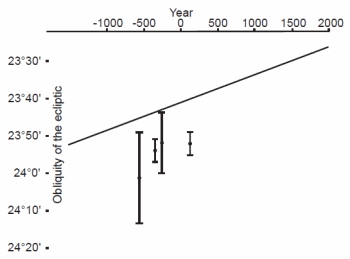
Fig. 11. Plot of Table 1 data.
What is the likely response of astronomers to these ancient data? It’s not as if these data haven’t been available. Likely they have been ignored because they don’t fit what we know today, with the rationale that the errors involved were so great. However, the errors would have to be on the order of ten arc minutes or more. This is a sixth of a degree. While this is small, the eye can discern angles on the order of a minute or two of arc. Tycho Brahe, the famous 16th century Danish astronomer, was able to make measurements of this accuracy with instruments that were only marginally improved over those available to the ancient Greeks (Tycho died a few years before the invention of the telescope). We don’t know how ancient Greek instruments compared to that of Tycho, but, in my opinion the errors of the ancient astronomers is not great enough to explain this discrepancy.
Conclusion
I have examined the methodology that Dodwell employed in developing his hypothesis that the earth was subjected to a catastrophic change in its tilt in 2345 BC, an alleged catastrophe that the earth has recovered from as recently as 1850. In a few instances I have had difficulty in replicating Dodwell’s results. In other cases Dodwell was a bit overzealous in extracting data and uncritically relied upon secondary sources. With no discussion of errors in the observations, it appears that he treated his data with near infinite precision. Dodwell’s hypothesis is highly dependent upon early measurements of the obliquity of the ecliptic that are not supported by Egyptologists. From these considerations, I consider the Dodwell hypothesis untenable. Despite these defects, a skeptical analysis that I have conducted here has left a few data points that are difficult to square with the conventional understanding of the obliquity of the ecliptic over time. While I cannot rule out that in the past the earth’s tilt was altered by some yet unknown mechanism, neither can I confirm it. The most reliable ancient data do not demand the sort of catastrophic change in the earth’s tilt with a gradual recovery that Dodwell maintained, so there is great doubt that this alleged event happened. If such an event actually happened, we cannot fix the date of that event with any certainty. Creationists are discouraged from embracing the Dodwell hypothesis.
References
Brennand, W. 1896. Hindu astronomy. London, United Kingdom: Charles Straker and Sons.
Dodwell 1. Retrieved from https://web.archive.org/web/20130519150537/http://www.setterfield.org/Dodwell_Manuscript_1.html.
Dodwell 3. Retrieved from https://web.archive.org/web/20130609044102/http://www.setterfield.org/Dodwell_Manuscript_3.html.
Dodwell 4. Retrieved from https://web.archive.org/web/20130609043949/http://www.setterfield.org/Dodwell_Manuscript_4.html.
Dodwell 5. Retrieved from https://web.archive.org/web/20130128191425/http://www.setterfield.org/Dodwell_Manuscript_5.html.
Dodwell 6. Retrieved from https://web.archive.org/web/20130128175943/http://www.setterfield.org/Dodwell_Manuscript_6.html.
Dodwell 7. Retrieved from https://web.archive.org/web/20121210121209/http://www.setterfield.org/Dodwell_Manuscript_7.html.
Dodwell 8. Retrieved from https://web.archive.org/web/20130127125252/http://www.setterfield.org/dodwell_manuscript_8.html.
Dodwell 9. Retrieved from https://web.archive.org/web/20121107003943/http://www.setterfield.org/Dodwell_Manuscript_9.html.
Dodwell table. Retrieved from https://web.archive.org/web/20130609044453/http://www.setterfield.org/Dodwell%20main%20chart.html.
Hamilton, H. C. and W. Falconer. 1854–1857. Strabo’s geography in three volumes. London: Henry G. Bohn. Retrieved from http://books.google.ca/books?id=K_1EAQAAIAAJ http://books.google.ca/books?id=KcdfAAAAMAAJ http://books.google.ca/books?id=0cZfAAAAMAAJ
Laskar, J. 1986. Secular terms of classical planetary theories using the results of general relativity. Astronomy and Astrophysics 157:59–70.
Lockyer, J. N. 1894. The dawn of astronomy: A study of the temple-worship and mythology of the ancient Egyptians. London, United Kingdom: Cassell.
Newcomb, S. 1906. A compendium of spherical astronomy with its applications to the determination and reduction of positions of the fixed stars. New York, New York: MacMillan.
Newton, R. R. 1973. The authenticity of Ptolemy’s parallax Data – Part I. Quarterly Journal of the Royal Astronomical Society 14:367–388.
Ptolemy. 1952. The almagest (Great Books of the Western World). Trans. R. C. Taliaferro. Chicago, Illinois: Encyclopedia Britannica.
Shaltout, M. and J. A. Belmonte. 2005. On the orientation of ancient Egyptian temples: (1) Upper Egypt and Lower Nubia. Journal for the History of Astronomy 36, no. 3: 273–298.
Smart, W. M. 1977. Textbook on spherical astronomy, 6th ed. Cambridge, United Kingdom: Cambridge University.












