Research conducted by Answers in Genesis staff scientists or sponsored by Answers in Genesis is funded solely by supporters’ donations.
Abstract
Some recent creationists have attempted to address the light travel time problem indirectly with an implied appeal to a small universe. If the universe is no more than a few thousand light years in size, then the light travel time is eliminated almost by definition. Here I survey the methods used for establishing astronomical distances. The only direct method of measuring stellar distances generally results in reliably measured distances of less than a thousand light years. However, that limit likely soon will exceed 6000 light years. Indirect methods already produce distances that are thousands, millions, and even billions of light years. The indirect distance determination methods ultimately are tied to direct determinations of distance, and they are reasonably consistent with one another. Furthermore the indirect methods are supported by well-understood physics. It is extremely unlikely that these methods are so wrong that the light travel time problem can be answered with a small universe.
Keywords: light travel time problem, parallax, magnitudes
Introduction
The recent creation model is that the earth and the rest of the universe were created supernaturally in six normal days a few thousand years ago and that the Flood in Noah’s time was global and universal. This is contrary to what is held by most scientists, who believe that the earth and universe are billions of years old. The size of the universe is a challenge for the recent creation model. Though they appear related, the large size of the universe and deep time are distinctly different concepts. If the universe is only a few thousand years old, then it would seem that today we could see objects out to a distance of at most a few thousand light years. Astronomers think that many objects are millions or even billions of light years away. To many people, the fact that we can see objects at such distances is strong evidence that the universe is indeed billions of years old. Recent creationists have called this “the light travel time problem.”
As I have previously argued, the light travel time problem often is improperly formulated (Faulkner 2013). Most discussions of this issue ask how we can see astronomical objects more than 6000 light years away, when in reality anything more than two light days away is a problem. The nearest star is a little more than four light years distant, yet Adam needed to see stars only two days after their creation. Ultimately, appealing to a universe that is only a few light years in size may suffice to explain how we can see stars today, but it fails to explain how Adam would have seen any stars at all.1 Any solution for the light travel time problem must account for Adam seeing the stars as evening fell at the conclusion of Day 6.
Creationists have responded to the light travel time problem with several possible solutions. For instance, in my recent paper (Faulkner 2013) I presented the Dasha’ solution.2 Setterfield (1989) suggested that the speed of light was very great in the beginning but rapidly decayed, allowing the light from the most distant parts of the universe to arrive as early as the end of the Creation Week. Humphreys (1994) has suggested that the universe began with a white hole rather than a big bang. In this model, relativistic effects caused billions of years to pass in much of the universe, but only a few thousand years on and near the earth. More recently, Hartnett (2008 and references therein) also has used general relativity, but with an alternate metric. Another recent solution is the Anisotropic Synchrony Convention of Lisle (2010). One of the most popular answers is to posit that God created a fully functioning universe, with light created in transit (Akridge 1979, DeYoung 2010). Each of these suggested resolutions have their good and bad points, a topic that I will not discuss further here.
Others have questioned whether the distances in astronomy really are as great as generally thought (for instance, see Armstrong [1973], Niessen [1983]). They point out that the only direct method of finding distances in astronomy may be applicable for distances of no more than a few hundred light years. All other methods that give much greater distances are indirect and thus are subject to many assumptions, not to mention errors. The implication is that if the assumptions are incorrect or that the errors are much greater than thought, then there are no truly large distances in the universe. If that is the case, then the universe at most may be a few thousand light years in size, and light from the most distant regions could have arrived at the earth by now.
How reasonable is this approach? There are at least two problems. First, it fails to answer the properly formulated light travel time problem as I discussed above. Second, it fails to adequately address the great distances involved in astronomy. In what follows I will explore various methods of finding distances in astronomy. Because distance determination methods beyond the solar system rely upon distances within the solar system, I briefly discuss solar system distances first. I will spend far more time discussing methods used to find the distances within the Milky Way galaxy, mostly to stars, and then consider extragalactic methods. I will present the most commonly used ones, plus a few of the more specialized ones. This is not an exhaustive study, for I will omit some of the more specialized distance determination methods. In each case I will discuss the assumptions and likely errors. I will evaluate the errors to see if they may accumulate so as to yield a universe far smaller than usually thought.
Solar System Methods
The ancient Greeks attempted measurements of the sizes and distances of the moon and sun. The best ancient work on this subject was that of Aristarchus of Samos (310–230 BC). Aristarchus determined that the angle that we observe between the moon and sun at the moon’s quarter phases was 87°, and from geometry he concluded from this that the sun must be 18–20 times farther away than the moon. Because the sun and moon appear about the same size in the sky, this result also implied that the sun must be 18–20 times larger than the moon. The earth’s shadow during a lunar eclipse is circular (because the earth is a sphere), and Aristarchus estimated that the moon is about ⅜ the size of the earth’s shadow. Combining all this information in geometric construction, Aristarchus determined the sizes and distances of the sun and moon compared to the earth’s size. He found that the moon was about ⅓ the diameter of the earth but that the sun’s diameter was about seven times the earth’s diameter.3 Aristarchus was the first person that we have record of being a heliocentrist, and many surmise that his conclusion about the sun being far larger than the earth influenced him to reach that conclusion. However, Aristarchus had seriously underestimated the distance of the sun, for the angle between the quarter moon and sun is far closer to 90°, with result that the sun is 400 times farther away than the moon (and 400 times larger). Nevertheless, the ancient values were accepted until a few centuries ago. Around 200 BC, Eratosthenes accurately measured the diameter of the earth (Faulkner 1997), which allowed computation of absolute sizes and distances for the sun and moon.
The first person to determine the relative distances of the planets from the sun was Nicolaus Copernicus (1473–1543). He did this in his book, De Revolutionibus (On Revolutions), published in 1542. His book was very influential in providing an argument for the simplicity of the heliocentric model as compared to the geocentric Ptolemaic model. However, Copernicus did more than that in his book; he used several centuries of data to determine the true relative orbital periods and orbital sizes of the naked eye planets, Mercury, Venus, Mars, Jupiter, and Saturn. No one had done this prior to Copernicus, because up to that time nearly everyone was a geocentrist, and such a computation was not possible in the Ptolemaic model. Mercury and Venus, orbiting closer to the sun than the earth, are inferior planets; the other three planets are superior planets. Fig. 1 shows the circumstances of how we view a superior planet. When a superior planet is on the other side of the sun as reckoned from the earth, and hence invisible to us, we say that the planet is in conjunction with the sun. When the planet is opposite the sun as seen from the earth, we say that the planet is at opposition. Notice that a superior planet is closest to the earth at opposition, so this is the best time to look at a superior planet.
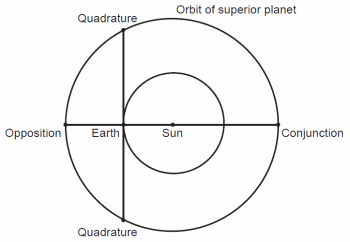
Fig. 1. Circumstances of viewing a superior planet.
Both the superior planet and the earth orbit the sun, but in Fig. 1 we can imagine that the earth does not move (this is geocentric). The length of time it takes for a planet to go from one conjunction with the sun to the next conjunction with the sun is the synodic period. The sidereal period, the true orbital period, is the length of time required for a planet to complete one orbit as viewed by an observer from outside of the solar system, or at least from the viewpoint of an observer who is not orbiting the sun as the earth is. Since the earth orbits the sun as do the other planets, it is not possible for us to measure directly a planet’s sidereal period. During one synodic period the earth will lap a superior planet, and Copernicus showed that the relationship between the sidereal period, P (in years), and the synodic period, S (in years), for a superior planet is
1/P = 1−1/S.
For the case of an inferior planet, the inferior planet laps the earth, so the relationship for an inferior planet is
1/P = 1 + 1/S.
Since Copernicus had data spanning several centuries, he was able accurately to calculate the sidereal periods of the five naked eye planets.
Partway between conjunction and opposition, a superior planet is at quadrature, meaning that the planet makes a right angle with the sun as viewed from earth. Notice that there are two quadrature points in Fig. 1. The arc length along the superior planet’s orbit between the two quadrature points that contains the opposition point is shorter than the arc length between the two quadrature points that contains the conjunction point. Assuming a near constant rate of revolution, a superior planet takes less time to go from one quadrature to the next while passing through opposition than it takes to go from one quadrature to the next while passing through conjunction. The larger an orbit is, the less difference there is between these two lengths of time. Assuming circular orbits (a close approximation in most cases), the ratio of these two lengths of time is related to orbital size. Copernicus was able to work out the relative sizes of the orbits of the three naked eye superior planets in terms of the earth’s orbital size.
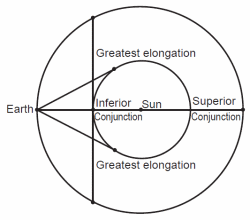
Fig. 2. Circumstances of viewing an inferior planet.
Similar reasoning applies to the inferior planets. The circumstances of an inferior planet are shown in Fig. 2. Notice that an inferior planet cannot be at opposition to the sun, nor can it be at quadrature. However, an inferior planet can be at conjunction with the sun two ways, when the planet passes between the earth and sun and when the planet passes on the other side of the sun. When between the earth and sun we say the planet is at inferior conjunction and that it is at superior conjunction when on the other side of the sun. When an inferior planet makes the greatest angle with the sun as seen from the earth, we say that the planet is at greatest elongation. Notice that there are two points of greatest elongation, one east of the sun and one west of the sun. The arc length between the greatest elongation points containing inferior conjunction is shorter than the arc length between the two greatest elongation points containing superior conjunction. Assuming constant speed, it takes less time for an inferior planet to travel from one greatest elongation to the other while passing through inferior conjunction than it does to pass from one greatest elongation to the other while passing through superior conjunction. The ratio of those two time intervals is related to the size of the orbit of the inferior planet. In a manner similar to computation of the superior planets, Copernicus was able to determine the sizes of the orbits of the two inferior planets.
With centuries of recorded data, Copernicus was able to compute the orbital sizes and periods of the then known planets with considerable accuracy. Those values stood for some time. The only limitation was that the orbital sizes were known in terms of the earth’s orbital size. The astronomical unit (AU) is defined to be the earth’s orbital size, or the average distance of the earth from the sun. While the average distances of the other planets from the sun (in astronomical units) were well determined, the astronomical unit itself was not. As mentioned above, Aristarchus had measured the astronomical unit, but had seriously underestimated it. A few other ancient Greeks had similarly computed the astronomical unit. Best known was Claudius Ptolemy (AD 90–168), whose result was similar to Aristarchus’s, and his was the value used throughout the Middle Ages.
With the invention of the telescope, the measurements of the astronomical unit greatly improved and approximated the modern value. People soon realized that the infrequent transits of Venus across the sun offered a good way to determine the astronomical unit’s length.4 The method is to observe Venus’s transit at two widely separated points on the earth. The known distance between the two points of observation is the baseline of a triangle. The difference in path and/or the duration of the transit from the two locations provides the angle opposite the baseline. Solution of the triangle using trigonometry allows computation of the earth-Venus distance at the time of the transit. The earth-Venus distance at transit was already known in astronomical units, from which the length of the astronomical unit follows. Jeremiah Horrocks (1618–1641) attempted to do this during the Venus transit of 1639, and, while his value was an improvement over previous estimates, it fell short of the modern value. The next transits of Venus were in 1761 and 1769, and a concentrated international effort allowed successful measurements of the astronomical units that are close to the modern accepted value. This was repeated at the transits of Venus in 1874 and 1882. In 1895 Simon Newcomb (1835–1909) combined data from these transits with measurements of the aberration of starlight and the speed of light to obtain the best measurement of the astronomical unit up to that time. The observed parallax of the minor planet 433 Eros near the earth in 1900–1901 and again in 1930–1931 allowed additional refinement. This method was similar to the Venus transit method in that it allowed the measurement of the earth-Eros distance in kilometers, which, since that distance was already known in astronomical units, allowed calibration of the astronomical unit.
There was another pair of Venus transits in 2004 and 2012, and the next one won’t be until the twenty-second century, but, while interesting, they don’t attract the scientific attention that they once did. The reason is that 50 years ago astronomers began to use radar reflected off the surfaces of solar system bodies to accurately measure their distances. Since the distances are known in astronomical units, this allows determination of the astronomical unit. These methods are far more precise than what we can learn from Venus transits.
Stellar Distances
Trigonometric parallax
Radar ranging doesn’t work to find the distances of stars, because stars are so incredibly far away that any return signal would take many years and would be very feeble. The only direct method of finding stellar distances is trigonometric parallax. As the earth revolves around the sun each year, we change our vantage point from which we view stars (see fig. 3). Our change in location causes the apparent position of a nearby star to shift slightly with respect to more distant stars. Surveyors on the earth use the same principle to measure the distance to remote objects or the altitudes of high mountains. With stars, we define the baseline to be the radius of the earth’s orbit, which is only half the total change in our position (the diameter of the earth’s orbit). Thus we define the parallax angle to be half the observed total angular shift. Let π be the parallax.5 If a is the radius of the earth’s orbit and d is the distance to the star, then by the small angle approximation
π = a/d.
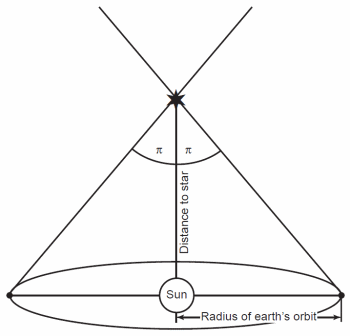
Fig. 3. Trigonometric parallax.
If π is measured in seconds of arc, then with an appropriate change of units we can write the above equation
π = 1/d,
where the appropriate unit of distance for d is the parsec (pc). We choose this unit and this name, because it is the distance required for a star to have a parallax of one second of arc. A pc is equal to 3.09 × 1013 km or 3.26 light years. Obviously the nearest stars will have the largest parallaxes. The nearest star (Proxima Centauri) is 1.3 pc away, which corresponds to a parallax of 0.″76.6
Friedrich Bessell (1784–1846) measured the first parallax in 1838. The star that he measured was 61 Cygni. For much of the nineteenth century astronomers used a filar micrometer attached to a telescope to measure parallaxes. A filar micrometer has two thin lines (usually spider web) viewed through an eyepiece. At least one of the lines can be moved by a screw with very fine threads. A filar micrometer allows very precise measurements of small angles, such as those required in parallax measurements. At the beginning of the twentieth century astronomers switched to photography. The standard procedure for measuring parallax has been precision measurements of the position of a target star with respect to background stars on photographs taken at six month intervals, on either side of the earth’s orbit around the sun. To do this, astronomers constructed measuring engines with very fine threaded screws to move an eyepiece over the photographic plates. Any difference in position is the result of parallax. Traditional parallax measurement done in this manner is very tedious, so what is the selection process for appropriate candidate stars for further study? Astronomers pick high proper motion stars from proper motion studies. I will explain proper motion in the next section.
Under good conditions the error in traditional parallax measurements has been about 0.″01. Because a parallax of 0.″01 would yield a distance of 100 pc, many people erroneously conclude that trigonometric parallax works to a distance of 100 pc. Even some astronomy textbooks have gotten this wrong. Suppose that we measure a star’s parallax to be 0.″01. The computed distance would indeed be 100 pc, but the 0.″01 error implies that the actual parallax could be anywhere between 0.″00 and 0.″02. These extremes correspond to distances anywhere from 50 pc to infinity. Obviously such a result is meaningless. Consider a measurement of 0.″05, which corresponds to a distance of 20 pc. Since 0.″01 is 20% of 0.″05, this measurement will have an error of 20%. Thus we can say that traditional ground based parallax is reliable (within 20%) to a distance of 20 pc (65 light years). Note that this relative error will increase for smaller parallaxes (greater distances). However, distances on the order of 20 pc by themselves are no problem for a recent creation. Roughly 760 stars have had their distances determined with this accuracy using classical techniques from the ground, which probably is about 20% of the total number of stars within 20 pc of the sun.
Modern technology has revolutionized parallax studies. CCD (charge coupled device) cameras replaced traditional photography before the end of the twentieth century. Charge coupled devices are far more sensitive than photographic emulsions. Since a charge coupled device records a digital image, computers have replaced measuring engines, saving much labor. Additionally, there have been several very specialized experiments developed for measuring parallax to much greater precision than before, but many of these have very limited application. Up to this point the greatest limitation on all parallax measurements has been the blurring effects of the earth’s atmosphere. Parallax measurements took a huge leap forward when the European Space Agency (ESA) launched Hipparcos (HIgh Precision PARallax COllecting Satellite) in 1989. Hipparcos had a 3½ year mission, and it was specifically designed to use the near perfect observing environment of space to obtain very accurate positions, parallaxes, and proper motions of a huge number of stars with unprecedented accuracy. We now have reliable distances of stars out to nearly 1,000 light years (Perryman et al. 1997). The original Hipparcos catalogue contained nearly 120,000 stars. In similar manner, the location of the Hubble Space Telescope (HST) above the earth’s atmosphere and its superb optics make it a suitable instrument to measure highly accurate parallaxes, though its heavy use for other research projects limit that amount of time for positional work.
Building on the success of Hipparcos, European Space Agency plans the launch of Gaia late in 2013. The Gaia mission has several objectives, including obtaining accurate distances of millions of stars out to tens of thousands of light years. This information ought to provide a very good 3-D map of much of the galaxy. If successful, for the first time direct distance measurements will exceed the light travel time limit of the recent creation model. This would of course eliminate any real possibility that the light travel time problem could be solved simply by appealing to a smaller than thought universe.
Moving cluster parallax
There are many star clusters in our galaxy, the Milky Way. A star cluster is a gravitationally bound group of stars. There are two types of star clusters, open clusters and globular clusters. Open star clusters contain hundreds or even thousands of stars, but globular clusters contain between 50,000 and a million stars. All stars have some motion, which astronomers call space motion. Space motion is divided into two components, radial and tangential velocities. The radial velocity is along our line of sight, and we easily measure it by Doppler shifts in lines in a star’s spectrum. The tangential velocity is perpendicular to our line of sight and is much more difficult to measure. Over time, the tangential velocity will cause a star’s position in the sky to change slightly. Measurements of stellar positions made over several years allow us to determine the rate at which a star’s position changes. We call this rate of change the proper motion, indicated by the Greek letter mu, μ. Proper motion is expressed in arc seconds per year. Barnard’s Star has the greatest proper motion, 10.4″/yr. Proper motions tend to be largest for nearby stars and virtually zero for very distant stars. As previously mentioned, proper motion surveys have provided the most likely candidates for the laborious task of measuring parallax. Proper motion surveys typically are done by comparing wide-field photographs of stars taken years, or even decades, apart. Unlike parallax, which is cyclical, proper motion accumulates over time, so photographs made over several years or decades give a large baseline over which to measure proper motions very accurately. While we can measure radial velocities directly via the Doppler Effect, we must know the distance to convert proper motions into tangential velocities. If the distance, d, is expressed in pc, and the tangential velocity, VT, is expressed in km/s, then the relationship is
VT = 4.74μd.
The members of a star cluster have space velocities that are roughly parallel because they share a common motion. The parallel space motion and the principle of perspective cause the proper motions to appear to converge or diverge at some point in the sky (see fig. 4). This is the same effect of perspective that makes the parallel rails of a train track appear to meet near the horizon. The point where the proper motions appear to intersect is the convergent point. The angle between any given star in the cluster and the convergent point is the same angle that is between the star’s radial velocity and space velocity. The complement of this angle is the angle between the space velocity and the tangential velocity. Knowing the angle and radial velocity allows us to compute the tangential velocity, and since the proper motion is known, we can infer the distance. In practice, astronomers apply this method to as many members of the cluster as possible, and average the results.
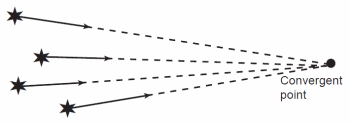
Fig. 4. Proper motion of cluster stars appear to converge at one point.
As with trigonometric parallax, moving cluster parallax has a limited range. For many years astronomers had successfully applied this method only to the Hyades star cluster (42 pc) and to two groups (a group is much more extended and loosely bound than a cluster and has fewer stars than a cluster). Until the Hipparcos mission, the moving cluster parallax method was far more important in calibrating other methods. Now that Hipparcos has greatly improved trigonometric parallax, this method is not quite as important. Hipparcos has recalculated the distance to the Hyades as 46 pc and has used the moving cluster parallax method to measure the distance to a total of ten open star clusters. Other studies involving different techniques and telescopes (including the Hubble Space Telescope) gave similar results for the Hyades. The average of these results, 47 pc, is now the standard distance to the Hyades. Moving cluster parallax does not work beyond a few hundred light years, so this method of finding distances does not present a direct problem for a recently created universe. If Gaia is successful, the moving cluster parallax method may fall into disuse, though it may be useful in providing checks of consistency of other distance determination methods.
Distance modulus, distance equation, and standard candles
Astronomers use the magnitude system to measure stellar brightness. Magnitude is measured on a logarithmic scale. The magnitude system has the added peculiarity of being backwards. That is, larger numerical magnitudes correspond to fainter stars. If two stars have intensities of I1 and I2, then the magnitude difference is
m2−m1 = −2.5 log(I2/I1).
The magnitude system is calibrated by the adoption of standard stars having defined magnitude values, so accurately measuring a star’s apparent magnitude is a straightforward process.
Apparent magnitude is how bright a star appears on earth, which obviously depends upon how bright the star actually is (its intrinsic brightness) and its distance. Astronomers use absolute magnitude to express the intrinsic brightness of a star. The definition of absolute magnitude, M, is the apparent magnitude a star would have if its distance were 10 pc. The difference between the two magnitudes, m-M, is the distance modulus and is related to the distance, in parsecs, by the equation
d = 10(m-M+5)/5.
Therefore, if we know the absolute magnitude of a particular star, we can find its distance by measuring its apparent magnitude and using the above distance formula. We shall see later that there are standard candles for which we think that we know M. That information with the above equation yields the distance.
Statistical parallax
There are classes of stars for which we believe that the members of the class have similar absolute magnitude. An example would be stars of the same spectral and luminosity class.7 Another example would be RR Lyrae variables, which I will discuss later. If we consider the members of such a homogeneous group of stars within a narrow range of apparent magnitude, then we conclude that they must lie at some mean distance. We can ascertain the mean distance by measuring the radial velocities and proper motions of the selected group of stars. It is also necessary that we know the location of the solar apex, the direction in which the sun is moving through space. Proper motion studies long ago revealed the solar apex.8 We can use the mean distance and mean apparent magnitude to determine the absolute magnitude of any member of the sample from the above equation. Once we know the absolute magnitude of any particular star in the group that we are considering (not necessarily in our sample to establish the mean distance), we can use the distance formula to find the distance.
Statistical parallax does not yield the confidence that comes from trigonometric parallax measurements, so we use the former only when the latter fails. Statistical parallax methods have been very useful in calibrating some of the indirect methods, such as the RR Lyrae variable method and the Cepheid variable method. With the improvements in trigonometric parallax from Hipparcos, a few RR Lyrae stars and Cepheids can be measured directly, so the method of statistical parallax is less important now. Again, if Gaia is successful, there probably will be no more need for the statistical parallax method.
Cluster main sequence fitting
The Hertzsprung-Russell (HR) diagram is a plot of the luminosities of stars versus their temperatures (see Faulkner and DeYoung 1991 for a discussion of the HR diagram). Fig. 5 shows a schematic Hertzsprung-Russell diagram. A Hertzsprung-Russell diagram can plot other quantities, such as absolute magnitude vs. spectral type or color. When considering a group of stars at the same distance (such as in a star cluster), the Hertzsprung-Russell diagram may be a plot of apparent magnitude vs. color. The easiest way to measure stellar temperature is with color. We generally use colored filters in magnitude measurements. A hot star will appear brighter in the blue part of the spectrum than in the red. Conversely, a cool star will be brighter in red than in blue (see fig. 6). The difference in magnitude measured in two different parts of the spectrum is a color. The most common color is B-V, where B is a blue magnitude and V is a visual (yellow-green) magnitude where the human eye is most sensitive.9 A plot of magnitude versus color is a color-magnitude (CM) diagram. The most common type of color-magnitude diagram is V versus B-V. One might expect that such a plot would show no correlation between the two variables, but most stars fall along a diagonal path that astronomers call the main sequence (MS). The hottest stars usually are the brightest, and the coolest generally are the faintest. Most stars lie along the main sequence. Those that lie above the main sequence are very large, so we call them giants, while those that lie below are very small, and we call them white dwarfs.
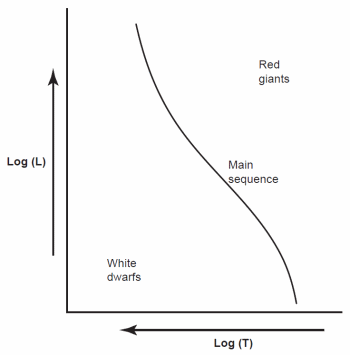
Fig. 5. Schematic Hertzsprung-Russell diagram.
Obtaining a color-magnitude diagram of a star cluster is a matter of observation. Unless the cluster is very far away and hence faint, we can identify the main sequence. Assuming that the main sequence of each cluster represents the same sort of stars, comparison of the main sequence for different clusters will reveal the relative distances. For instance, if one cluster has a fainter main sequence than another cluster, then we conclude that the fainter cluster has a greater distance. If we know the distance to any one cluster, then we can establish the absolute magnitude of the main sequence at any color. We say that the main sequence is calibrated. We may compare the main sequence of a cluster for which we do not know the distance to the calibrated main sequence. The amount of shift between the two is the distance modulus, from which we can calculate the distance.
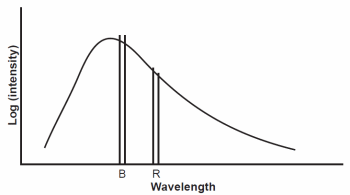
Fig. 6. The spectrum of a hot star. B indicates the blue band pass, while R indicates the red band pass.
An example will illustrate this method. For decades we have known the distance to the Hyades cluster by the moving cluster method. Before Hipparcos, neither trigonometric parallax nor the moving cluster parallax method could be used to find the distance of the Pleiades star cluster. Fitting the main sequence of the color-magnitude diagram of the Pleiades to the color-magnitude diagram of the Hyades revealed a distance of about 140 pc. Astronomers measured the distance of other open clusters the same way. The distance of the Pleiades determined by Hipparcos is 118 pc. Other post-Hipparcos studies have found distances closer to 140 pc, which has resulted in controversy that has not yet been resolved. The range in values for the Pleiades is less than 20%, but that is higher than expected. In the case of the ten clusters for which Hipparcos has measured distances, the old distances are usually within 20% of the improved ones.
While this method is simple in principle, there are subtle factors for which we must apply corrections. The upper portion of the main sequence is missing from most clusters. Astronomers attribute this to differences in age, with the oldest clusters missing the greatest amount of the upper main sequence. Secular astronomers think that the Hyades is a few billion years older than the very young Pleiades, so the color-magnitudes of the two clusters overlap only on the lower main sequence. The double cluster h and χ Persei have a portion of the main sequence that the Pleiades lack. Most astronomers attribute this to these star clusters being even younger than the Pleiades.
Another problem is with the observed magnitudes and colors themselves. As light passes through the interstellar medium (ISM), it encounters dust, which scatters some of the light. The greater the distance or the dustier the environment through which the light passes, the greater the scattering. Scattering dims light, an effect that we call extinction. If a star has been dimmed, then we think that the star is farther than it actually is, so extinction causes us to overestimate distances. Therefore, we must account for extinction. This may seem hopeless, but observations and theory reveal that interstellar dust scatters shorter wavelength (bluer) light more efficiently than longer wavelength (redder) light, and so obscured stars appear redder than they would otherwise. This should not be confused with red shift, where the photons have their wavelengths shifted to greater values. With interstellar reddening, the flux is depressed, but more in the blue than in the red part of the spectrum so that the stars appear redder than they actually are. The result is that starlight is not only dimmed but is reddened as well, and the amount of dimming is proportional to the amount of reddening that occurs. Therefore, if we can determine the amount of reddening, we can correct both the observed color and magnitude for interstellar extinction. There are several ways to determine how much reddening that a star has endured.
From the study of stellar structure and atmospheres we know that composition affects the colors of stars also. Most stars are about 75% hydrogen by mass, with helium making up most of the remainder. The remaining few percent or less are made of all other elements, which astronomers collectively call metals. The variable Z gives the percentage of metal abundance. A low metal composition causes the main sequence to shift in color toward the blue, the amount of shift being proportional to Z. Within a cluster observations show that the composition does not vary much, so measurement of Z for a few stars is sufficient to establish the metalicity for the cluster. We can do this with detailed spectral study or by Stromgren photometry.10 Stellar models tell how much to correct the color-magnitude diagrams for composition.
To summarize the cluster main sequence method, we first obtain a color-magnitude diagram for a star cluster. From the metal abundance, we correct the color, which is a horizontal shift of the main sequence. An estimate of interstellar extinction allows a blueward shift in color and an upward shift in magnitude. Now we compare the corrected color-magnitude diagram to a calibrated color-magnitude diagram to determine how much vertical shift is required to cause the magnitudes to agree. This shift is the distance modulus, from which we calculate the distance. We calibrate the lower main sequence knowing the distance to the Hyades, as well as by using nearby field (non-cluster) main sequence stars for which we know distances from trigonometric parallax measurements. The cluster main sequence fitting method is a bootstrapping operation that plays a key role in calibrating other methods. The inherent errors are certainly greater than those for good parallaxes, but probably within 20%. This method can be used for any cluster for which we can observe the main sequence. Astronomers have measured the distances of many open clusters this way, usually resulting in distances of thousands of light years or less. Globular clusters on the other hand have distances from 10,000 ly to many tens of thousands of light years. Many globular clusters are in the outlying parts of our Milky Way galaxy. So when used to its limits, the cluster main sequence method presents a difficulty for a universe only a few thousand years old, and it is not likely that the expected errors can change the situation.
Cepheid variable method
Cepheid variable stars are giant pulsating stars named for the prototype δ Cephei, which John Goodricke (1764–1786) discovered was a variable star in 1784. Cepheids regularly change brightness by up to two magnitudes with very regular periods. The range of Cepheid periods is between two days and two months. Cepheids have distinctive light curves characterized by a rapid rise to maximum brightness followed by a more gradual decline back to minimum brightness. Fig. 7 shows a schematic Cepheid variable light curve. Henrietta Leavitt discovered their significance as a distance determination method in 1912 while studying them in the Small Magellanic Cloud (SMC) and the Large Magellanic Cloud (LMC). The Small Magellanic Cloud and Large Magellanic Cloud are two small satellite galaxies of the Milky Way in which many of the brighter stars are easy to observe. She noticed that the average apparent magnitudes of Cepheids in either galaxy were directly proportional to the logarithm of their periods. From the small apparent sizes of the Small Magellanic Cloud and Large Magellanic Cloud it is evident that any differences in distance within them are small compared to the overall distance to the Clouds. In other words, all of the stars in the Small Magellanic Cloud or the Large Magellanic Cloud are at approximately the same distance. Thus differences in apparent magnitude must result from real differences in absolute magnitude. Therefore there must be a period—luminosity (P-L) relation for Cepheids, a point that we miss when considering Cepheids nearby in our galaxy because of large differences in distance. Fig. 8 shows a schematic P-L relationship for Cepheid variables.
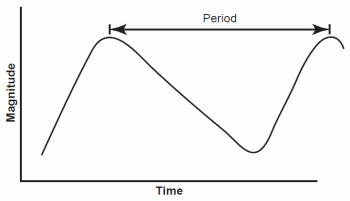
Fig. 7. Typical Cepheid variable light curve.
To use this fact to measure distances requires that we calibrate the P-L relation. We can do this if we know the distance to at least a few Cepheids from some other method, preferably from trigonometric parallax. Unfortunately, Cepheids are so rare that none of them lie close enough for direct measurement by classical techniques, and so astronomers used other methods for a long time. A few Cepheids are found in star clusters, and so the cluster main sequence method could be used to calibrate the P-L relation, but statistical parallax has been the preferred method. The Hipparcos mission has allowed the direct measurement of the parallax of a number of Cepheids. The earlier calibrations were changed by about 10%. It is unlikely that the Gaia mission will change the calibration much, but we shall see.
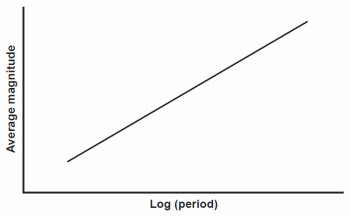
Fig. 8. A schematic period luminosity relation for Cepheid variables.
During the 1950s astronomers discovered that there are two types of Cepheids, Type I, or classical Cepheids, and Type II, or W Virginis stars. The Type II Cepheids are about 1.5 magnitudes fainter than the Type I Cepheids. Because Cepheids are quite luminous, we can see them at great distances, and they provide a crucial link in establishing the extra- Galactic distance scale. Most of the more distant Cepheids are of type I, but the method was originally calibrated with type II. When the two types of Cepheids were recognized, it caused the perceived size of the universe to roughly double. Until the Hipparcos mission astronomers feared that the P-L relation might have errors as great as 20 or 30%. The fact that that was not the case gave great confidence that another major re-calibration such as occurred during the 1950s is not likely. Cepheid variables within the Milky Way galaxy can have distances of tens of thousands of light years, so this method of finding distances places some pressure on a recent creation. The situation is worse when applied to extragalactic distances.
RR Lyrae stars
RR Lyrae stars are named for the prototypical star, RR Lyrae. RR Lyraes are pulsating variables with many similarities to Cepheids. They are on the horizontal branch to the upper right of the main sequence, but are lower in the Hertzsprung-Russell diagram than the Cepheids. Both Cepheids and RR Lyrae stars lie in the instability strip of the Hertzsprung-Russell diagram where pulsating stars are. RR Lyrae stars have amplitude of about a magnitude, while their periods are between 0.3 and 0.7 days. Unlike the Cepheids, however, they do not follow a P-L relation, but instead they all have about the same average absolute V magnitude. Currently we think that their absolute V is +0.75. This calibration largely comes from Hipparcos data, for several RR Lyrae stars were in the Hipparcos data set. This calibration was an improvement over the calibration from statistical parallax (none were close enough for classical, ground-based parallax measurements). There is a small correction for metalicity, Z. Furthermore, there is a weak P-L relation in wavelengths other than V. Knowing that all RR Lyrae stars have about the same absolute magnitude, it is obvious that they offer an excellent opportunity to measure distances wherever we see them. Measurement of the apparent magnitude, m, gives the distance modulus, m−M.
Though RR Lyraes are too faint to effectively use for finding distances to other galaxies, we observe them throughout our galaxy. These variables are very common in globular star clusters, so they are sometimes called cluster variables. Thus they are the prime method for finding distances to globular clusters. The nearest globular cluster is about 10,000 ly away, and others are well over 50,000 ly distant. Therefore the RR Lyrae method clearly suggests that the universe is larger than a few thousand light years.
Spectroscopic parallax
Using the various methods of finding stellar distances, we can construct a calibrated Hertzsprung-Russell diagram. This fixes the absolute magnitude of various parts of the Hertzsprung-Russell diagram, such as the main sequence, white dwarfs, and the several types of giant stars. At some points, theory of stellar structure and atmospheres must be used in constructing a calibrated Hertzsprung-Russell diagram. Turning the process around, if we can deduce the location of a star on the Hertzsprung-Russell diagram by some means, then we can infer the star’s absolute magnitude. We directly measure the apparent magnitude, and so we know the distance modulus and hence the distance.
We often can learn the location of a star on the Hertzsprung-Russell diagram from spectroscopy. The presence and strengths of various absorption lines determine a star’s spectral type, which is related to temperature or color. The width of the spectral lines reveal how large a star is (I will discuss the basic physics of this later). The size fixes the star’s location on the Hertzsprung-Russell diagram for a given spectral type. This method is rather crude and is generally used when other methods are not possible. This is true of non-variable field stars (that is, stars that are not in clusters).
Binary star method
This method can proceed a couple of different ways. A visual binary is a binary system in which both stars are visible. The stars slowly orbit one another, often taking decades to do so. From the orbital motion of either star we find the masses of the stars, provided that we know the distance to the system. We can turn the process around: if we estimate of the masses of the stars, then we can treat the distance as the unknown. We can infer the masses of the stars by observing the spectral types and by assuming that they have similar properties as other stars of the same types. This process is called the method of dynamic parallax, and since is applies only to visual binary stars, it is obviously of limited use.
Another method involves the very few visual binaries that are also spectroscopic binaries. A spectroscopic binary is one in which the motions of the stars are detected by their Doppler shifts. From the speeds of the stars we can determine the sizes of the orbits, and from the angular sizes of the orbits we can calculate the distance. Both of these methods using visual binary stars are of only limited use, but they do offer some checks upon the other methods.
Eclipsing binary stars offer another method of finding distances. An eclipsing binary star is a binary star system where we view the orbit nearly edge-on so that the stars pass in front of (eclipse) one another every revolution. The stars are too close together to be seen separately, so their light fuses into a single image. However, the periodic eclipses diminish the amount of light that we receive. A light curve is a plot of the amount of light received as a function of time throughout a complete cycle. Analysis of an eclipsing binary light curve allows us to model the system and determine such quantities as the sizes (radii) of the stars involved.
The brightness of a star depends upon the size and temperature of the star. We may determine temperature a number of ways, such as spectral classification or the photometric color (a result from the photometric data used to create the light curve). The Stefan-Boltzman law states that the emission per unit area goes as the fourth power of the temperature, while the surface area goes as the square of the radius. Thus the luminosity, L, is
L = 4πR2 σT4,
where σ is the Stefan-Boltzmann constant. We can use stellar atmosphere models to convert the luminosity to an absolute magnitude. We easily can combine the absolute magnitudes of the two stars in the binary system into a single absolute magnitude. The difference between the calibrated apparent magnitude and the absolute magnitude is the distance modulus, from which we find the distance. While this method generally will give us the distance to an individual binary star, this method becomes very important when applied to binaries in external galaxies, which I will discuss shortly.
Geometric methods
A supernova remnant is a cloud of hot gas rapidly expanding from the site of a supernova. Several supernova remnants are known, but the best example is the Crab Nebula. The Crab Nebula coincides with the position of a supernova that the Chinese recorded in the year 1054. Astronomers have extensively studied the Crab Nebula. For instance, there are Doppler shifts in the spectrum of the Crab Nebula that indicate that gas is moving both toward and away from us at speeds of up to 2000 km/s. The best interpretation is that the Crab Nebula has a three-dimensional shape and that gas on the edge of the nebula nearest us is moving toward us and gas on the opposite side is moving away from us. At the same time, comparison of photographs made a few decades apart reveal that knots of material in the nebula are moving laterally outward as well (perpendicular to our line of sight). If we assume that the remnant is roughly spherical, then we can equate the measured line of sight Doppler motion with the tangential velocity. As I discussed earlier, the tangential velocity, VT, the proper motion, μ, and the distance, d, are related by the equation
d = VT/4.74 μ.
Thus we can find the distance, but further consideration allows us to find the time since the supernova explosion and the size of the supernova remnant as well.
From any photograph of the Crab Nebula, one can see that it is not spherical. Assuming that it is a prolate spheroid as suggested by the photographs, one obtains a distance of about 2,000 pc, an origin date of AD 1140 (as would be observed on earth—the eruption itself would have been some time prior to this) and a diameter of a few light years. The good agreement (within a little more than 10%) with the observed origin date of 1054 gives us confidence in the distance and size. There may have been some slowing of the expanding material, which, if corrected for, would improve the fit to the date. Overall, this appears to be a good distance determination method, albeit somewhat restricted in use. Astronomers have used a similar procedure to find the distance of Nova Persei by studying an expanding shell of gas that appeared after its 1901 outburst. Astronomers used a similar method to measure the distance to SN 1987A, a supernova seen in 1987. The derived distance is the same as determined by other methods for the Large Magellanic Cloud, the host galaxy of the supernova.
Pulsar distances by dispersion
The name “pulsar” was coined in 1967 for the then newly discovered objects that rapidly pulsed, or flashed, radio emission. Today astronomers know of thousands of pulsars, and they frequently discover new ones. Pulsar periods range from a little more than a millisecond to a few seconds. We think that a pulsar is a rapidly rotating neutron star with a very strong magnetic field carried along by its rotation. The relative speed between material near the surface of neutron star and the magnetic field may be a significant fraction of the speed of light. The rapidly moving magnetic field accelerates charged particles so that they emit radiation that is beamed along the axis of the magnetic field. If we happen to lie near the cone swept out by the rotating magnetic field, then we periodically view down toward a magnetic pole of the neutron star (and hence the beam of radiation) and experience a pulse of radiation. Therefore, the period of the pulsar is the same as the rotation period of the pulsar. This explanation of pulsars makes specific predictions about the radiation that agree with observations. For instance, the radiation from a pulsar is polarized and has a characteristic synchrotron spectrum, as predicted by theory. One of the first pulsars discovered was the famous one in the Crab Nebula. The Crab Pulsar flashes 30 times per second. The coincidence of the Crab Pulsar with a supernova remnant was a key clue in concluding that a neutron star is one of the two possible objects left behind by a supernova (the other is a black hole). The Crab Pulsar is important for other reasons as well.
Pulsars radiate by tapping their considerable rotational kinetic energy. In this respect they act as flywheels. As their rotational kinetic energy is radiated away, pulsars slowly increase their periods as they age (astronomers observe small period increases in pulsars). With so much stored energy, pulsars can last a very long time, but not so supernova remnants. Supernova remnants expand and dissipate, so their lifetimes are far shorter than pulsar lifetimes. Therefore not all pulsars are embedded in supernova remnants. Nor do all supernova remnants have pulsars inside. There are at least three reasons for this. First, some supernovae result in black holes, not neutron stars. Second, since our ability to see a neutron star as a pulsar depends upon our lying near the cone swept out by the neutron stars’ magnetic field, we obviously don’t see most neutron stars as pulsars. Third, there is some evidence that some pulsars are ejected from the site of the supernova by an asymmetrical explosion. An example of a possible pulsar runaway is PSR 1758-23 and the supernova remnant W28.
Pulsars usually are close to the galactic plane, where the material in the interstellar medium is densest. Much of the visible light of a pulsar is absorbed by dust in the interstellar medium, making optical identification of the pulsar or any associated supernova remnant impossible in many cases. However, the radio emissions are not affected by dust very much, so we may observe pulsar radio emissions from considerable distance. On the other hand, charged particles (mostly electrons) in the interstellar medium do affect radio emissions. The speed of propagation of radio waves is slowed slightly by the electrons, with the amount of slowing depending upon the frequency. High frequency waves are less affected than low frequency waves. Therefore, if we simultaneously observe pulses at various wavelengths, we find that the pulses observed at lower frequencies are delayed slightly from pulses observed at higher frequencies. Astronomers call this effect dispersion.
The amount of dispersion also depends upon the column density of electrons, which is the product of the average number density of electrons and the distance. If we measure the dispersion and know the average number density of electrons between a pulsar and us, we can find the distance. Astronomers believe that the average electron number density is 0.028/cm3. This figure was derived from the measured dispersion and known distance of the Crab Pulsar. This is why the Crab Pulsar is a very important object. This method relies upon the assumption that the number density of electrons is reasonably uniform in the interstellar medium and that we know what the average value of the number density is. Given the relatively large distance to the Crab Pulsar we have confidence that the derived number density of electrons probably is a good average. Most pulsar distances measured by this method are less than 2000 pc, the distance to the Crab Pulsar. Some of the nearby pulsars could have average number densities that deviate from the assumed average, which would of course affect the distance determination. It is unlikely that the error in any case is as much as a factor of two.
Extra-Galactic Distances
Other galaxies are so far away that only the brightest individual stars are visible, and then only in the nearest galaxies. Until recently, only the Cepheid variables among the methods described in the previous section were possible with other galaxies. Most extra-galactic distance determination methods rely upon establishing some sort of standard candle; that is, concluding that there is some class of very bright objects for which we know the intrinsic brightness, or absolute magnitude. If we measure the standard candle’s apparent magnitude, then we find the distance modulus, and hence the distance.
Eclipsing binaries
As previously mentioned, the Milky Way galaxy has two small satellite galaxies, Large Magellanic Cloud and the Small Magellanic Cloud. At distances of perhaps 160,000 and 200,000 light years, respectively, the Large Magellanic Cloud and Small Magellanic Cloud represent very important steps in establishing extra-galactic distances. For instance, the P-L relation was discovered in the Large Magellanic Cloud and Small Magellanic Cloud. Many Cepheids are readily visible in the Magellanic Clouds, and they are used here to calibrate that and other methods. Unfortunately, there has been some disagreement over the distances to the Large Magellanic Cloud and Small Magellanic Cloud, which introduces uncertainty in the calibrations of many other methods. To sort this out, Guinan et al. (1998) used the Hubble Space Telescope to observe an eclipsing binary star in the Large Magellanic Cloud. From the earlier discussion of eclipsing binary stars, we saw that we can find the absolute magnitudes of the stars involved. When compared to the apparent magnitude, the distance easily follows. The distance of the Large Magellanic Cloud that they found (166,000 ly) was similar to the distance that had been established for decades, but was about 20,000 ly less than a more recent distance from the improved calibration of the Cepheid method with the Hubble Space Telescope. The discrepancy (a little more than 10%) has not been resolved. Astronomers have determined the distances of several other eclipsing binary stars in the Large Magellanic Cloud, Small Magellanic Cloud, M31, and M33. These are the closest galaxies of any size.
Extra-galactic Cepheid variables
Because Cepheids are intrinsically very luminous (M = −6 for the brightest), astronomers can identify them in the nearest galaxies. As discussed earlier, we calibrate this method in our own galaxy, and so it represents the important transition from stellar to extra-galactic distances. Of course we make the assumption that the Cepheids seen in other galaxies are similar to the ones in the Milky Way. The re-calibration of the 1950s was a result of the realization that we were seeing a different type in other galaxies than the type used to calibrate the method. At first this may seem a promising avenue of pursuit if one wishes to scale back the great extragalactic distances. However this will not work unless quite serious revision is done. Currently the Cepheid method is used to fix extra-galactic distances to a few tens of millions of light years. A revision like that of the 1950s would change these distances by only a factor of two, far too small to have real consequence for recent creation.
As previously discussed, Hipparcos directly measured the distances of some Cepheids. For the sake of argument, let us ignore the Hipparcos results. With that assumption, no Cepheids can have their distances measured by parallax, so they all must be at least 20 pc away. A few of the brightest appearing Cepheids are quite bright, of naked eye brightness in some cases. The ones visible in nearby galaxies are about 20 magnitudes fainter, implying that they must be about 108 times fainter. By the inverse square law this means that the faint Cepheids in other galaxies must be 10,000 times farther away than the nearby Cepheids. If the nearby Cepheids are just beyond parallax measurement, say 100 ly, then the extragalactic ones must be roughly a million light years away. The only way this distance can be reduced to a few thousand light years is to deny that what we think are extra-galactic Cepheids are Cepheids at all, but rather are some other sort of fainter pulsating stars. This raises a number of problems. What kind of stars are they? Why don’t we see them nearby? Why don’t we see other types of stars, such as the sun, in other galaxies? With the largest telescopes and modern detectors, stars like the sun should be visible to a distance of more than 100,000 ly, yet we do not see these stars in other galaxies. Yet the spectra of the combined light from these galaxies appear to match that of solar type stars. This suggests that solar type stars are very numerous in these galaxies.
We usually express extra-galactic distances in megaparsecs (Mpc), or one million parsecs. One Mpc is then 3.26 million ly. Until the Hubble Space Telescope the Cepheid distance method worked out to a distance of about 6 Mpc, far enough to measure the distances of about 30 of the closest galaxies. The Hubble Space Telescope has extended the upper limit of the Cepheid variable method to nearly 25 Mpc, which includes hundreds of galaxies. This range includes the Virgo Cluster of galaxies, an important step in establishing the extra-galactic distance scale. This was one of the key projects for the Hubble Space Telescope.
Brightest stars
The most luminous stars are super giants that are brighter than the Cepheids, and so are visible at greater distances. The most luminous seem to have an absolute magnitude of about −9. So if we can identify the few brightest stars in a galaxy and measure their apparent magnitudes, then we know the distance modulus, and hence the distance, of the galaxy. With the Hubble Space Telescope this method works to a distance of about 200 Mpc, whereas before the Hubble Space Telescope it worked to a distance of about 25 Mpc. This obviously is a crude method, depending upon the accuracy to which we know the absolute magnitude of the brightest stars. The error inherent in this method could easily be on the order of 100%, but this does not mean that this method has nothing to say about light travel times. An error of 100% amounts to a factor of two. To reduce a distance of 100 million ly to 10,000 ly would require an error of a million percent, which is obviously not the case.
Novae
Novae is the plural of the word nova, which comes from a Latin word meaning “new.” Since ancient times astronomers have known novae as stars that suddenly appear without warning and then fade. They are not actually new stars, but are stars that temporarily flare up to thousands of times brighter than usual. At one time astronomers thought that a nova was an exploding star, a misconception that persists with the public. Today astronomers believe that novae occur in binary systems in which the stars are close together and one of the stars is a white dwarf. Mass transfer from the companion star results in a build-up of hydrogen on the surface of the white dwarf. Eventually thermonuclear detonation of the hydrogen occurs, which is the observed brightening. The process of hydrogen accumulation and detonation repeats many times. Many types of novae are recognized today, with some recurring every few days or even within a few minutes. The amount of brightening is directly related to the period between outbursts, so that the ones that recur frequently brighten by only a small amount, while the classic novae brighten the most and probably take thousands of years to repeat. Thus, novae of all types represent a continuum.
For our purposes here, we are concerned with the classic bright novae. At peak, the brightest novae are about 10 times brighter than the brightest Cepheids, and so we may observe them in nearby galaxies. Thus we can use this method to determine distances a little greater than the Cepheid method, but not as far as the brightest super giant method. Because it is not as well calibrated as the Cepheid method, it has more error. The Cepheid variables play a role in calibrating this method. If both Cepheids and a nova are seen in a nearby galaxy, the distance to the galaxy as established by the Cepheids gives the distance to the nova. This distance gives that nova’s absolute magnitude, and if all bright novae have about the same absolute magnitude, the method should work. A nova is a relatively rare event, but with monitoring of many galaxies, it is not unusual to find them.
Extra-galactic globular clusters
Globular clusters contain 50,000 to perhaps a million stars. They have a spherical symmetry that gives them the appearance of large balls, hence the name. The absolute magnitudes of globular clusters in the Milky Way and the Andromeda galaxy (M31) follow a Gaussian distribution. Astronomers call this distribution the globular cluster luminosity function (GCLF). The globular cluster luminosity function’s of the Milky Way, M31, and members of the Virgo Cluster of galaxies are similar, suggesting that there may be a universal globular cluster luminosity function. Knowing the distances of individual globular clusters in the Milky Way and the distance of M31, astronomers calibrate the globular cluster luminosity function in absolute magnitude. This allows astronomers to measure the distance of any other galaxy by measuring its globular cluster luminosity function. The difference of the galaxy’s globular cluster luminosity function and the calibrated globular cluster luminosity function is the distance modulus. There probably is no truly universal globular cluster luminosity function, so by assuming that there is may introduce an error of 20% in distance. Secondarily, astronomers can use the apparent sizes of globular clusters to find the distance to the host galaxy. Globular clusters appear to have a tight distribution in size, so by measuring the apparent sizes of globular clusters in other galaxies, we can calculate the distances of the galaxies.
Planetary nebulae
Planetary nebulae are clouds of gas that were ejected from stars via winds. Astronomers think that this process is the transformation of a red giant star into a white dwarf star (Faulkner 2007). Similar to globular clusters, astronomers have found that the luminosities of planetary nebulae follow a Gaussian distribution, and they call this the planetary nebula luminosity function (PNLF). We can see planetary nebula in nearby galaxies, so calibration of the planetary nebula luminosity function allows us to find the distances of the host galaxies, provided that planetary nebula luminosity function of other galaxies is similar to that of the Milky Way and M31.
HII Regions
HII refers to singly ionized hydrogen, HI being neutral hydrogen. An HII region is a large region around hot, bright stars in which the hydrogen is ionized. The hot, bright stars are necessary to produce enough ultraviolet photons to maintain the ionization. The electrons recombine with the protons to form hydrogen atoms and in the process emit photons of light, some in the visible Balmer series. Reionization and recombination repeatedly occur, so that an HII region appears very bright. The Great Orion Nebula (M42) is an example of an HII region.
The total brightness of an HII region depends upon the number and type of stars that are powering it, as well as the density of the gas. Thus the luminosities of HII regions vary over a large range. However, some studies have shown that the linear sizes of the largest HII regions are about the same from one galaxy to another of the same type. Like the globular cluster and planetary nebulae methods, this can give us a standard candle. This method is at least as crude as the globular cluster method, but it should work to about the same distance as the brightest super giant method.
Supernovae
As the name suggests, supernovae are eruptions in stars that are much more energetic than those of ordinary novae. Based upon differences in observed light curves and spectra, there are two basic types: type I and type II, with type I having subclasses a, b, and c. Astronomers think that type II, type Ib, and type IIc supernovae are explosions of high mass stars caused by the catastrophic collapse of their cores. Type Ia supernovae appear to originate in interacting binary stars where one of the members of the system is a white dwarf that accretes enough material from its companion to exceed the Chandrasekhar limit. The Chandrasekhar limit is the maximum mass that a white dwarf may have, and is a little more than 1.4 times the mass of the sun. When a white dwarf exceeds this limit it catastrophically collapses into a much smaller neutron star or is completely disrupted. The collapse is accompanied by a tremendous release of energy that is we see as the supernova.
Both theory and observations suggest that type Ia supernovae have about the same absolute magnitude at maximum brightness.11 This uniformity and extreme brightness makes them an excellent standard candle. At maximum brightness supernovae can outshine an entire galaxy, at absolute visual magnitude of −19.3. This is 10,000 times brighter than the brightest super giants, and so supernovae should be visible about a hundred times farther away than super giants. Assuming that we have properly calibrated the brightness of supernovae and assuming that supernovae in other galaxies are similar to ones in or near our galaxy, we can use them to find the distances of galaxies in which supernovae are observed. Despite their lack of uniformity, type II supernovae can now be used with what is called the expanding photosphere method.
Problems of the supernovae method stem from doubts about the calibration, questions about the uniformity of supernovae, and the often decades-long wait between supernovae in any particular galaxy. Given these caveats, this is still a very powerful method in that we can see supernovae over such great distances (more than a billion light years). To solve the problem of the rarity of supernovae, a network of robotic telescopes takes images of many different galaxies each night. The system quickly compares the images to archival images to find any supernovae that may have happened. When the system finds a supernova, it instantly relays that information to major observatories so that astronomers can measure the brightness and obtain spectra of the supernovae. This effort has netted many supernovae. In 2013 the Hubble Space Telescope detected a type Ia supernova about ten billion light years away. In 1999 data from type Ia supernovae played a key role showing that the rate of expansion in the universe may be speeding up, an effect attributed to dark energy. These very powerful methods of finding distances are obviously difficult to reconcile with a creation only a few thousand years old.
Tully-Fisher relation
The Tully-Fisher relation, pioneered in the late 1970s, is a very useful way to measure the distances of spiral galaxies. Spiral galaxies, such as the Milky Way, contain large, cool, rarified clouds of neutral hydrogen (HI regions). Under such conditions electrons mostly are in the ground state, but they may undergo a highly forbidden transition from the parallel to the antiparallel spin state with respect to the proton. Each transition is accomplished by the emission of a photon at a wavelength of 21 cm, which is in the radio part of the spectrum. This radiation is easily observed, and for decades radio astronomers have used 21 cm emission to map out the spiral structure of the Milky Way.
This emission is very sharp, but because of the orbital motions of the clouds about the center of a galaxy, the emissions are Doppler shifted so that the 21 cm emission from a galaxy is broadened. The amount of broadening depends upon the speed of the revolving clouds, which, since the clouds are following Keplerian motion, depends upon the mass of the galaxy. The amount of mass in a galaxy should be directly related to the amount of stars, and hence to the total brightness of the galaxy. Therefore there should be a direct relation between the intrinsic brightness of a galaxy and the broadening of the 21 cm emission. The calibration of this relation is accomplished by observing nearby galaxies, for which distances can be measured by other methods. Use of this method requires measurements of 21 cm emission broadening and the apparent magnitude of a galaxy. A correction to the broadening must be applied by measuring the angle by which the plane of the galaxy is inclined to our line of sight. This can be measured from a photograph of the galaxy. In recent years astronomers have discovered that this method works best in infrared rather than visual.
Because elliptical galaxies lack hydrogen gas clouds, the Tully-Fisher relation does not work for them. However astronomers have developed a similar method for ellipticals that makes use of the velocity dispersion of stars that exists in such systems. The integrated spectrum of a galaxy is that of the combined light of all of the stars in the galaxy. Because stars have absorption spectra, the integrated spectrum of a galaxy is also an absorption spectrum. Rather than a broadening in an emission line, the orbital velocities of the stars produces broadening in the profiles of absorption lines in the spectra of ellipticals.
The errors of distances determined by the Tully-Fisher relation depend upon the calibration (which is based upon other distance determination methods) and upon the accuracy of the assumption that similar type galaxies of the same mass have similar luminosities. Variations of 10 or 20% in the luminosities of similar mass galaxies could easily be the case, but we do not expect that they would be any greater than this. Both errors probably would not approach 100%. Overall this method is very powerful, because of the great distances over which we can measure the dispersion.
Hubble relation
The Hubble relation probably is the best known method of determining galaxy distances, and undoubtedly it is the method most distrusted by many recent creationists. Edwin Hubble discovered his famous relation in 1929, based upon the understanding that the universe likely is expanding. Objects that are moving fastest with respect to us ought to be the greatest distance away from us. Therefore there should be a linear relation between the distance and radial velocity:
V = HD,
where V is the radial velocity,12 D is the distance, and H is the constant of proportionality (the Hubble constant). Due to either expansion or velocity moving away, absorption lines in a spectrum are shifted to longer wavelengths. Longer wavelengths are toward the red end of the spectrum, so we call this redshift. Astronomers have spent much effort in determining the value of H, because once we know it we may reverse the process to find the distance of any galaxy for which we measure its redshift. To find the calibration we must measure the redshifts and distances (by other methods) of a number of galaxies. The greater the number of galaxies and the larger the range in their distances used in the calibration process, the more confidence that we have in the constant.
The original value of H determined by Hubble was 550 km/s/Mpc, but by 1960 the value was down to 50 km/s/Mpc. The Hubble relation remained unchanged until the early 1990s. Today astronomers think that H is about 70 km/s/Mpc. Revisions of H came about through improved methods and better understanding, but also through better handling of the data. For instance, different researchers can obtain different values of H because they weigh the data differently. The 1990s saw much work in the determination of H. One of the key projects for which the Hubble Space Telescope was constructed was to better determine the Hubble constant. The increase in the value of H in the early 1990s caused a decrease in the estimated age of the big bang universe and a re-evaluation of the ages of globular clusters.
Any redshift measurement is a combination of expansion and true Doppler motion. When using the Hubble relation to determine the distance of a faraway galaxy, the expansion term dominates the redshift, so the Doppler motion isn’t important. However, for nearby galaxies the Doppler motion easily may exceed the expansion term. But nearby galaxies are the ones for which we have reasonably confident distances and hence are used for calibrating H. Therefore to determine H one must account for the Doppler motion inherent in the nearby (and hence low redshift) galaxies. How to adequately handle this problem has been a major part of the disagreement over the value of H. It should be kept in mind that use of the Hubble relation is an extrapolation, but this does not necessarily invalidate its use. The Hubble relation generally is the only method by which we can measure the distances of quasars, the most distant objects in the universe.
Since the 1960s the Hubble relation has come under attack from Halton Arp. His work will not be discussed here, but suffice it to say that he has presented evidence that calls into question the trustworthiness of redshifts to relate distances. Most astronomers dismiss Arp’s work mostly because of its implications for cosmology: the big bang theory demands that redshifts be cosmological. For this reason many recent creationists applaud Arp’s work. However, this support from recent creationists stems in part from the failure to fully understand Arp’s position. Arp doesn’t dispute that in general the Hubble relation works; he merely questions the slavish application of the Hubble relation for all galaxies and quasars. Even if the Hubble relation does not work in every case, there is strong evidence that, in general, redshift is proportional to distance.
Given these caveats and assuming that Arp is wrong, what is the error when using the Hubble relation? Doppler shifts can be accurately measured and local velocities are insignificant at great distances, so the greatest error should occur because of uncertainty in the value of the Hubble constant. Over the past half century the measurement of H has varied by less than a factor of two, and it is not likely to vary by more than that. Therefore it is unlikely that distances measured with the Hubble relation could be in error by more than a factor of two.
Brightest galaxies in clusters
Galaxies tend to associate together in groups, or clusters. Within a cluster there is a large range in brightness among the members, but it appears that from cluster to cluster the brightest members have about the same total luminosity. This is very similar to the situation for stars, for which the brightest super giant stars in any galaxy are about as luminous as the brightest super giants in any other galaxy. Just as that fact can be used to estimate the distances of galaxies, the brightest galaxies in a cluster can be used to measure distances to the cluster. This is a very crude method, usually giving relative distances, so it has only limited use. It can be used when other methods fail, finding particular application for very distant clusters, which are too faint to have a Doppler shift measured by spectroscopy.
Geometric methods
Earlier we saw that the expansion of gases in a supernova remnant may be used to find the distance to the remnant. If similar motions can be observed in extra-galactic objects, then geometric methods can be used to find the distances of the objects. At extra-galactic distances any transverse motion will not be detectable in the optical part of the spectrum. However, in the radio portion of the spectrum several radio telescopes widely separated around the world may be combined to produce a single image having the effective resolution of a telescope nearly the size of the earth. This is called very long baseline interferometry (VLBI). This allows for very accurate relative positional work, and so large transverse motions can be measured in the radio spectrum. One of the first applications of this method was to the galaxy NGC 4258 (Hernstein et al. 1999).
Discussion
Table 1 is a list of the distance determination methods that I have discussed here, along with rough estimates of the upper limit of distance that these methods can be used. Some of these limits are merely estimates. Many of these limits are likely to increase.
Table 1. List of distance determination methods with rough limits of use.
| Method | Range |
|---|---|
| Radar ranging | Within the solar system |
| Trigonometric parallax | 1,000 light years |
| Moving cluster parallax | 500 light years |
| Statistical parallax | A few thousand light years |
| Cluster MS fitting | A few thousand light years |
| Cepheid variables | 50 million light years |
| RR Lyrae variables | 100,000 light years |
| Spectroscopic parallax | Thousands of light years |
| Binary star method | Thousands of light years |
| Geometric methods | 100 million light years |
| Pulsar dispersion | 50,000 light years |
| Eclipsing binaries | A few million light years |
| Brightest stars in galaxies | 600 million light years |
| Bright Novae | 150 million light years |
| Globular clusters in galaxies | 50 million light years |
| Planetary nebulae in galaxies | A few million light years |
| Bright HII regions in galaxies | 50 million light years |
| Type Ia supernovae | 10 billion light years |
| Tully-Fisher relation | 100 million light years |
| Hubble relation | Billions of light years |
| Brightest galaxies in clusters | Billions of light years |
The size of the solar system does not present recent creation with a light travel time problem. I have reviewed 10 stellar and 12 extra-galactic distance determination methods. Trigonometric parallax is the only direct method, but it works to a relatively short distance, with new techniques extending this to a maximum of nearly 1000 ly. This is no problem for recent creation of only a few thousand years, but it is a problem for recent creation if the light travel time problem is properly formulated. However, the Gaia mission probably will extend the direct method of determining distances out to tens of thousands of light years. If Gaia is successful, then this will be a problem with a universe only a few thousand light years in size. Other indirect methods for finding stellar distances extend beyond this distance, and at their limits of use they place some pressure on the concept of a recent creation. The errors inherent in the indirect methods easily could be 30% or more, which cannot change the picture much either way. The many methods are bootstrapped and cross-checked so that they do give reasonable consistency and ultimately are calibrated to trigonometric parallax measurements. The reliability of many methods has been tested with results from the Hipparcos mission. In each case the calibrations were altered, but generally within the errors previously estimated. This is a good indication that most of the methods are reliable.
At this time the one stellar distance method that presents a tremendous light travel time problem is the Cepheid method. This is because it bridges from intragalactic to extra-galactic distances. The Cepheids in the Large Magellanic Cloud and the Small Magellanic Cloud played a crucial role in deducing the period-luminosity relation, and they certainly appear to be similar to galactic Cepheids. The Cepheids seen in more distant galaxies also appear to be similar in galactic ones. If this is true, then a simple calculation shows that the extra-galactic Cepheids are at least two orders of magnitude more distant than a young creation would seem to allow.
Some might question if these much fainter appearing Cepheids really are the same sorts of stars as the brighter appearing Cepheids. There are good physical reasons to conclude that these are all the same kind of stars. The absorption lines seen in the spectra of stars reveal not only composition, but more importantly, the temperature as well. The spectral lines of a particular element can be present only if the element is present in the star. However the absence of spectral lines does not mean that an element is not present in a star. The vast majority of stars are made almost entirely of hydrogen, but hydrogen lines are not seen in every star. The electronic transitions that cause hydrogen lines in the visible part of the spectrum require that a significant number of hydrogen atoms have electrons in the first excited state. The temperatures in the coolest stars are so low that nearly all of the electrons are in the ground state. In the hottest stars virtually all of the hydrogen atoms are ionized. Stars with intermediate temperatures have a sufficient number of electrons in the first excited state to produce hydrogen lines. Hydrogen lines strengths are at their maximum at a temperature of about 10,000 K. Similar principles apply for other elements as well. For instance, singly ionized metals have their peak near the temperature of the sun (a little less than 6000 K). Therefore the types and strengths of spectral lines reveal the temperatures of stars.
The widths of lines tell us the sizes of stars. Some stars have very broad spectral lines, while others have very narrow lines. There are several mechanisms that can broaden spectral lines, but the most important here is pressure broadening. Pressure broadening is caused by Doppler shifts of the atoms as they are jostled about by collisions due to the pressure in the gas in the atmospheres of stars. The greater the pressure, the greater the pressure broadening is. Stars must be in hydrostatic equilibrium. That is, the outward pressure and inward gravitational force must be balanced, or otherwise stars would quickly expand or contract. Therefore the amount of pressure broadening must be related to the gravity present in the atmosphere of a star. Stars of large radius have small gravity at their surfaces where spectral lines are formed, while small stars have strong gravity. Thus the widths of spectral lines tell us how large stars are. Super giants have the thinnest lines, giants a little more broad, main sequence stars more broad, and white dwarfs have the broadest of all. This effect is not just theoretical—it has been confirmed with stars for which we have found their radii by independent means.
When these principles are applied to Cepheid variables, we find that the faintest appearing ones are identical to the brightest appearing ones. That means that they must have the same temperatures and sizes. The intrinsic brightness, or luminosity, of a star depends upon the surface area and the fourth power of the temperature. The surface area goes as the square of the radius, so we can write this as
L = 4πR2 σT4,
where R is the radius, T is the temperature, and L is the luminosity. Similar reasoning may be applied to other types of stars as well. Therefore other methods of finding distances, such as spectroscopic parallax, appear to be solidly founded.
All of this reasoning is based upon well-understood and tested physics. Some could argue that the physics that works here might not work elsewhere. If this were true, then we could raise doubts about the physical principles involved. This approach undermines a basic assumption that makes science possible. We assume that there is universality about natural law. That is, how the universe operates here and now is how it has operated everywhere since creation (miracles excepted).13 Indeed some have argued that science is a western concept that could only have arisen under Christianity where it is understood that there is an underlying order imposed upon the universe by the Creator. Thus to argue against the universality of physical laws amounts to a very subtle attack upon what it is creationists are trying to argue in the first place.
Other than the Cepheid distance method, the extra-galactic distance measurement methods are less precise. Their calibration largely relies upon the Cepheid method, so any inherent errors in that method propagate in the others. This was illustrated by the doubling of the size of the universe in the 1950s. Additionally, each method has its own uncertainties, but it is unlikely that those amount to errors of 100% or more. This is not to suggest that these methods are useless, but rather that the distances could be off by a factor of two. Distances that are incorrect by a factor of 10 would require a 1000% error, while the factor of 100 mentioned above would require a 10,000% error.
Such large errors would be very difficult to accept. In most galaxies we do not see any individual objects (stars, star clusters, nebulae). Why? It is most reasonable to assume that the vast majority of galaxies are at such immense distances that we cannot see the individual objects. Only in nearby galaxies do we see individual objects, and even then we only see what appear to be the brightest stars and biggest clusters and nebulae. That is, with exception of their much fainter brightness and smaller size, these objects appear identical with the biggest and brightest objects in our galaxy.
To scale back the size of the universe to avoid the light travel time problem would require that we radically alter our understanding of various astronomical observations and astrophysical principles. For example, stars that appear to be Cepheids in nearby galaxies are not. Likewise, stars like the sun that appear to be common in the solar neighborhood and should be visible in nearby galaxies if they are much closer to us than is currently thought are somehow absent. Also, the spectrum of the integrated light of every other galaxy appears to be that of average stars that are rather common in the Milky Way, but this cannot be because they would be resolved easily if they were only a few thousand light years away.
What, then, are the galaxies that we see? For a long time astronomers thought that they were nebulae in our own galaxy, and hence not very far away. It was in 1924 that that Hubble first observed a few of the brightest stars in the Andromeda galaxy, establishing that it (and by inference other galaxies) was a stellar system in its own right. There is now abundant evidence that the Andromeda galaxy, as well as many other galaxies, truly are more distant than a few thousand light years. Though we may not know the distance to any galaxy with a lot of precision, the distance is known to be quite large.
Conclusion
In my survey of astronomical distance determination methods I have shown that we can have confidence that the universe really is as large as astronomers claim. To explain the light travel time problem by appealing to a universe much reduced in size is not tenable. Therefore, the light travel time problem is real, and it requires a real solution. Fortunately, we have a number of solutions already in the creation literature, but further proposals are welcome.
References
Akridge, G. R. 1979. The mature creation: More than a possibility. Creation Research Society Quarterly 16, no. 1:68–72.
Armstrong, H. L. 1973. “Light years” disappear. Creation Research Society Quarterly 9, no. 4:243.
DeYoung, D. B. 2010. Mature creation and seeing distant starlight. Journal of Creation 24, no. 3:54–59.
Faulkner, D. R. 1997. Creation and the flat earth. Creation Matters 2, no. 6:1.
Faulkner, D. 2004. Universe by Design. Green Forest, Arkansas: Master Books.
Faulkner, D. R. 2007. A review of stellar remnants: Physics, evolution, and interpretation. Creation Research Society Quarterly 44, no. 2:76–84.
Faulkner, D. R. 2013. A new solution to the light travel time problem. Answers Research Journal (in press).
Faulkner, D. R. and D. B. DeYoung. 1991. Toward a creationist astronomy. Creation Research Society Quarterly 28, no. 3:87–92.
Guinan, E. F., E. L. Fitzpatrick, L. E. DeWarf, F. P. Maloney, P. A. Maurone, I. Ribas, J. D. Pritchard, D. H. Bradstreet, and A. Giménez. 1998. The distance to the Large Magellanic Cloud from the eclipsing binary HV 2274. Astrophysical Journal 509, no. 1:L21–L24.
Hartnett, J. 2008. Starlight, time, and the new physics. In Proceedings of the Sixth International Conference on Creationism, ed. A. A. Snelling, pp. 193–203. Pittsburgh, Pennsylvania: Creation Science Fellowship and Dallas, Texas: Institute for Creation Research.
Harnett, J. 2011. Does observational evidence indicate the universe is expanding? Part 1: The case for time dilation. Journal of Creation 26, no. 3:109–114. Retrieved from http://creation.com/expanding-universe-1.
Hernstein, J. R., J. M. Moran, L. J. Greenhill, P. J. Diamond, M. Inoue, N. Nakai, M. Miyoshi, C. Henkel and A. Riess. 1999. A geometric distance to the galaxy NGC 4258 from orbital motions in a nuclear gas disk. Nature 400:539–541.
Humphreys, D. R. 1994. Starlight and Time. Green Forest, Arkansas: Master Books.
Lisle, J. 2010. Anisotropic synchrony convention—A solution to the distant starlight problem. Answers Research Journal 3:191–207. Retrieved from http://www.answersingenesis.org/articles/arj/v3/n1/anisotropic-synchrony-convention.
Niessen. R. 1983. Starlight and the age of the universe. Impact #121.
Perryman, M. A., M. A. C. Perryman, L. Lindegren, J. Kovalevsky, E. Høg, U. Bastian, P. L. Bernacca, and M. Crézé. 1997. The Hipparcos catalogue. Astronomy and Astrophysics 323, no. 1: L49–L52.
Setterfield, B. 1989. Minisymposium on the speed of light–Part IV. The atomic constants in light of criticism. Creation Research Society Quarterly 25, no. 4:190–197.










