The Velocity of Light and the Age of the Universe
Originally published in Creation 4, no 1 (March 1981): 38-48.
Much modern research in astronomy and physics is built on the assumption that the velocity of light is one of the few things that is truly consistent.
Summary
The author claims that computer analysis of the measurements of light velocity recorded since 1675 shows otherwise and points to a beginning—a creation of light and a subsequent slowing down of this created light. The date of this beginning appears to support the short Biblical chronology.
All computer work on this project was performed on the DEC 10 computer at the Flinders University in South Australia by Mr Trevor Norman, Tutor in Mathematics at the same university. His extremely valuable help in this project is hereby gratefully acknowledged.
If you propose that the universe and all in it is the product of an act of Creation only 6,000–7,000 years ago, many people ask—“How is it that objects millions of light years away can be seen? Surely such light would take millions of years to reach us.”
The question is a valid one and several types of answers have been proposed to it in the past with only limited success.
Some have proposed that both a star and the light from the star were created at the same time so that a star was visible instantaneously throughout the whole of the universe. This view is unable to resolve several of the problems which exist with respect to exploding stars or the behavior of quasars. It results in the apparent problem of having to believe that we are seeing some things that exist only in the form of light and never really happened.
Others have proposed that light does not travel through space in straight lines but along curved surfaces (Riemannian Space concept) so that in reality light can reach anywhere throughout the universe in approximately 16 Earth years. However, while the mathematics of Riemannian Space is fascinating, confirmation of this idea is lacking.
There is a third alternative which to date has not been explored, but which I believe solves not only many of the observational problems of astronomy and Genesis Creation, but has wide ranging implications for the whole of the physical sciences.
The basic postulate of this article is that light has slowed down exponentially since the time of Creation. This thought is radical and at first looks outside of confirmation. However, there are at least 40 observations of the speed of light since 1675 which support this suggestion.
The Velocity of Light 1675:1976
The values of the velocity of light (C) listed in Table 1 form the bulk of the data which I have used to investigate the concept of light decay.
Table 1
(For detailed discussion of the origin of these figures see Appendix 1).
| Values of C—Optical Methods Only: Units km/sec. | ||
|---|---|---|
| Romer | 1675 | 301,300±200 |
| Bradley | 1728 | 301,000 |
| 1871 | 300,400±200 | |
| Cornu-Helmert | 1874.8 | 299,990 |
| Michelson | 1879.5 | 299,910±50 |
| Newcomb | 1882.7 | 299,860±30 |
| Michelson | 1882.8 | 299,853±60 |
| 1885 | 299,940 | |
| Perrotin | 1902.4 | 299,901±84 |
| 1902.8 | 299,895 | |
| 1906 | 299,880 | |
| 1924 | 299,802±30 | |
| Michelson | 1926.5 | 299,796±4 |
| Mittelstaedt | 1928.0 | 299,778±10 |
| Pease-Pearson | 1932.5 | 299,774±11 |
| 1933 | 299,774±2 | |
| Anderson | 1937–41 | 299,771±12 |
| Huttel | 1940 | 299,768±10 |
| Values of C—Cavity Resonators | ||
| Essen | 1947 | 299,797±3 |
| Essen | 1950 | 299,792±3 |
| Hansen | 1951 | 299,789±1 |
| Values of C—Geodimeter | ||
| Bergstrand | 1949 | 299,796±2 |
| Bergstrand | 1951 | 299,793.1±2.5 |
| Scholdstrom | 1955 | 299,792.4±0.4 |
| Edge | 1956 | 299,792.4±0.11 |
| Values of C—Radio Interferometer | ||
| Florman | 1954 | 299,795.1±3.1 |
| Froome | 1958 | 299,792.5±0.1 |
| Values of C—Tellurometer | ||
| Wadley | 1956 | 299,792.9±2 |
| Wadley | 1957 | 299,792.6±1.2 |
| Values of C in km/sec.—Radio | ||
| Kraus | 1953 | 299,800 |
| Corson & Lorraine | 1962 | 299,790 |
| I.T.T. Staff | 1970 | 299,793 |
| 1972 | 299,792.5 | |
| Bay, Luther, White | 1972 | 299,792.462±0.018 |
| Nature, Sept. 8, 1972, pp. 65–66 | ||
| 1976 | 299,792.456 | |
Conclusions from Table 1
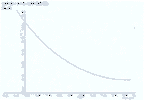
From the figures the drop in c is very evident, amounting to about 1507 km/sec. in 300 years. One additional feature is also striking, namely the rapid rate of tapering off in the rate of change of c per year. De Bray equated it to about 4 km/sec. on figures from 1870–1920; Tolles noted it at about 0.3 km/sec. per year about 1950. In addition it is worthy of note that the observed change in c over three centuries is far greater than the margins of error in the observations, the error in Romer’s value being only one sixth of the observed change in c. The above results compel me to formulate a new theory for the behavior of light.
The Decay curve of light
Table 2 below summarizes the data used to determine the decay curve. A large number of possible curves were tried to fit the observed data points. Exponential curves could not reproduce the observed rates of change at the different dates or the observed values. Generally these curves went below the points. Power curves, polynomials, logarithmic and hyperbolic functions were all tried with lack of success. There was only one curve tried which fitted the data points exactly and reproduced all of the observed features. Its general form is a log sine curve, with a logarithmic vertical axis, typical of most energy functions. The general equation is Log c = A + B (Log sine (T)) where A and B are constants that have the respective values of 5.47682068 and -1.94665385. It is of interest to note that this curve is similar to those accepted as decay curves of Novae and SuperNovae. The time function T expresses the years (t) of time elapsed since Creation in a scale of degrees. For example, if we take 6,000 years as being the complete range of the curve, these 6,000 years take up the 90 degrees of the Log sine scale so the transformation to obtain (T) in degrees is T = (t/l) x (90/6000): that is T = 0.015 t. Since the Flinders University computer was working in radians, the transformation was T = zt where z = 11/12000 = 0.261799387799 x (1/103), which gives T in radians.
One must, of course ask the question, has the change in the value of c been due to improved measurement techniques. A statistical analysis of this problem has been included in Appendix 3.
Table 2
| Date | (O) Observed Value km/sec. | (P) Predicted Value km/sec. | O-P |
|---|---|---|---|
| 1675.0 | 301,300±200 | 301,422.822 | -122.82 |
| 1728.0 | 301,000 | 300,871.492 | +128.51 |
| *1871.0 | 300,400±200 | 299,950.915 | +449.08 |
| 1874.8 | 299,990 | 299,937.669 | +52.33 |
| 1879.5 | 299,910±50 | 299,922.084 | -12.08 |
| 1882.7 | 299,860±30 | 299,911.979 | -51.98 |
| 1882.8 | 299,853±60 | 299,911.670 | -58.67 |
| 1885.0 | 299,940 | 299,904.970 | +35.03 |
| 1902.4 | 299,901±84 | 299,858.808 | +42.19 |
| 1902.8 | 299,895 | 299,857.889 | +37.11 |
| 1906.0 | 299,880 | 299,850.771 | +29.23 |
| 1924.0 | 299,801±30 | 299,818.366 | -16.37 |
| 1926.5 | 299,796±4 | 299,814.890 | -18.89 |
| 1928.0 | 299,778±10 | 299,812.925 | -34.93 |
| *1932.5 | 299,774±11 | 299,808.129 | -34.13 |
| *1939.0 | 299,771±12 | 299,801.29 | -30.29 |
| *1940.0 | 299,768±10 | 299,800.41 | -32.41 |
| 1947.0 | 299,797±3 | 299,795.825 | +1.17 |
| 1949.0 | 299,792.4±5.5 | 299,794.865 | -2.47 |
| 1949.0 | 299,796±2 | 299,794.865 | +1.13 |
| 1950.0 | 299,792.5±1 | 299,794.445 | -1.95 |
| 1950.0 | 299,793.1±1 | 299,794.445 | -1.35 |
| 1951.0 | 299,793.1±2.5 | 299,794.065 | -0.97 |
| 1951.0 | 299,794.2±1.4 | 299,794.065 | +0.13 |
| 1951.0 | 299,792.6±1.3 | 299,794.065 | -1.47 |
| 1953.0 | 299,800 | 299,793.429 | +6.57 |
| 1954.0 | 299,792.75±0.35 | 299,793.165 | -0.415 |
| 1954.0 | 299,795.1±3.1 | 299,793.165 | +1.935 |
| 1955.0 | 299,792.4±0.4 | 299,792.945 | -0.545 |
| 1955.0 | 299,792.0±6 | 299,792.945 | -0.945 |
| 1956.0 | 299,792.9±2 | 299,792.765 | +0.135 |
| 1956.0 | 299,791.9±2 | 299,792.765 | -0.865 |
| 1956.0 | 299,792.4 | 299,792.765 | -0.365 |
| 1957.0 | 299,792.6±1.2 | 299,792.625 | -0.025 |
| 1958.0 | 299,792.5±0.1 | 299,792.525 | -0.025 |
| 1062.0 | 299,790 | 299,792.445 | -2.445 |
| 1966.0 | 299,792.1±1 | 299,792.445 | -0.345 |
| 1967.0 | 299,792.56±0.11 | 299,792.445 | +0.115 |
| 1970.0 | 299,793 | 299,792.445 | +0.555 |
| 1972.0 | 299,792.462±0.018 | 299,792.445 | +0.017 |
| 1976.0 | 299,792.456 | 299,792.445 | +0.011 |
When did decay commence and finish?
The decay curve is quite sensitive to its date of origin. If this is set too early, the curve comes in below the early clusters of points. If the date is too late, it comes in above the observed values. The best date of origin for the curve as determined by the observational evidence is 4040 BC±20 years. This date of origin would refer to the time of Creation/Fall. In a similar manner the cutoff date beyond which there is a zero rate of change in the value of c (i.e. the data at which c becomes constant) is quite critically determined by the final cluster of points from about 1947 onwards. From these observations it would seem that beyond 1960 the speed of light had reached its minimum value and was constant thereafter.
This conclusion raises the obvious difficulty as to how one verifies a process which has occurred in the past but is not occurring in the present. To answer this, we would point out that the curve is solely dependent on actual dependent on actual observations and refer to Appendix 3 for confirmatory statistical treatment of this data.
In addition future articles will deal with how well the concept works to explain events past and present (especially ramifications on radioactive decay rates).
Application of a change in c
To give some idea of the trend of values, the speed of light was 391,966 km/sec. at AD 1 according to the curve. If we accept the short Biblical chronology of 1,656 years from Creation to the Flood, the curve predicts a value at the time of the Flood (2384 BC) of 1,621,908 km/sec. Thereafter the rise is steep. At 3540 BC the value was 15,783,104 km/sec. while at 3940 BC it touched 360,146,768 km/sec. The origin of the curve is virtually asymptotic, but a very good estimate of the actual initial value is given by the curve at one to 1.5 days from its origin. The speed of light was then about 1.5 x 1017 km/sec. or roughly 5 x 1011 faster than it is now. I will assume that this value held from the time of Creation until the time of the Fall, as in my opinion the Creator would not have permitted it to decay during his initial work. At the same time, I propose that this initial high value of c would have produced the appearance of great age to the universe in that one week (to those who look with eyes and minds fixed on the current value of c).
Integration over the curve shows that our initial problem of light traveling millions of light years in only 6,000 years, is solved and that one major problem associated with the quasars is overcome also. The total distance traveled by light since Creation would be about 12 x 109 light years.
It is interesting to note that the new determination of Hubbles Constant corrected for the movement of the local group of galaxies towards Virgo super cluster gives a new distance for the limit of the observable universe of 7-9 x 109 light years. Thus my proposed figures are in strict accord with recent findings. (See Appendix 2)
There is also now no problem with the movement of material in quasars faster than the current speed of light; indeed it is to be expected in objects so close in time to the Creation, and it is observed (See Science News, 110:40, 1976 and Nature 267:211–213, 1977). In addition to a number of others, quasar 3C 345 and quasar 3C 287 show this effect well; the former has two components flying apart at 2.5 times the current value of c, the latter has it several orders of magnitude greater according to some notes I have about quasars. This is no longer a problem. Likewise the periods of variability of the quasars do not indicate a small size which is the conclusion based on a fixed value of c and in apparent disagreement with their energy. Indeed, half a year after Creation c was still 1.08 x 1013 km/sec. or about 3.6 x 107 faster than now—traveling about 98,600 light years in 24 hours. As most large galaxies are about 100,000 light years across, it is not difficult to see how variations in intensity of light with a period of several days can be achieved for the whole object.
Conclusions
The general equation of the curve fitting the data points is Log c = A + B (Log sine (T)). It has its origin at 4040 BC and the speed of light then was about 5 x 1011 faster than now, a value which probably held throughout Creation week. The speed of light became constant about AD1960. In comparison to the data points, the predicted curve stands up well to four types of error analysis. The value of r2 is one to nine figures indicating a perfect fit to the data (See Appendix 3). The probable error given by the Observed values minus the Predicted values nearly always lies within the limits of experimental error. The plot of error bars proves it is not possible for c to have been constant since AD1675 (See Appendix 3). The average percentage error in the observations is 0.00785% which is only 1.6% of the total difference in measurement in 300 years. The problem of the total distance that light has traveled is solved as the curve shows the value to be about 12 x 109 light years in 6,000 years. The problem presented by quasars exhibiting speeds greater than the current value of c is solved as also is the short period of light variability of some of them when compared to their size. Thus a decrease in the value of c with time is not only in accord with observation, but also explains some otherwise unexplainable facts very adequately.
To be continued:
Subsequent articles propose to deal with the change in c and the atom; the drastic effect it has upon the half-lives of radioactive elements and hence upon radiometric dating; the way it causes the rapid apparent aging of stars; and cosmological considerations. In short, how it is that many of the appearances which are generally interpreted as indicating great age inevitably result from the high initial value of c.
Appendix 1
The values from 1871 to 1933 have been obtained from Science, 66:sup x, Sept. 30, 1927 by an author quoting M.E.J. Gheury de Bray who was commenting on the decreasing values of c in the official Journal of the Astronomical Society of France, L’Astronomie; Nature 133:464, 1934 by de Bray; Nature 134:771–772, 1934 by R.T. Birge. In all these articles the consistency of the drop in c was noted and an equation presented that approximated to the then current behavior of c. We have omitted two values from the presentation as both were obviously anomalous, one far too high, the other far too low by all standards and de Bray comments that the apparatus appears to have been faulty. The values from 1937 to 1957 come from “The Velocity of Light & Radio Waves” by Froome & Essen. The values in Table 1 have been grouped according to method of measurement so that the systematic trend is not masked by different means of measurement with different built-in biases. The most recent determinations of c have come using radio techniques and appeared in Ham Radio January 1980, p. 62 in an article by H.F. Tolles who concluded that c was changing at an average rate of about one third of a km/sec. per year over the last 20 or so years. The April 1980 edition of Ham Radio p. 6 included a letter by Keith Rhodes which concludes from the figures available that c was a variable constant. In the October 1975 issue of Scientific American p. 120, C.L. Stong questioned if c might change with time as science has failed to get a consistently accurate value. Pease & Pearson’s equipment was sufficiently sensitive to note a change in c over the period (about l 1/2 years) of the experiment. Froome & Essen commenting on the downward trend said that they could give no reason “to account for these discrepant results.” The Bradley value in 1728 of 301,000 km/sec. came from Froome & Essen. Sky & Telescope June 1973, 45:353 gave Romer’s 1675 value after reworking a selection of his data. The result was 0.5% above the current value i.e. 301,300. Froome & Essen placed it higher. The minimum value was used.
A significant number of the values in Table 1 came from experiments done in vacuo. Froome & Essen tabulate the results of indirect measurements of c such as parallel wires or the ratio of electromagnetic to electrostatic units. From the figures presented, with results varying widely by 1,000s of km/sec. over short times, it would appear that these methods are unreliable, involve other constants, and, as Froome & Essen point out, use assumptions which do not appear valid.
Appendix 2
These findings were announced by John Huchra of the Harvard-Smithsonian Center for Astrophysics and were commented upon by Dr George Shoot of the University of California. Reports were carried in the Adelaide Advertiser, November 16, 1979, p. 2, and the West Australian, December 14, 1979, p. 31 (see also Nature 270:9–10, 1977 etc.). In addition, the article in the C.R.S. Quarterly Vol. 16(3), pp. 176–181 by R. Akridge “The Expansion of the Universe” shows clearly that a correction to the Hubble Law must be applied, and, when this is done the observed distances are reduced even further.
Appendix 3
Is the change in light velocity due only to improved “measuring techniques”?
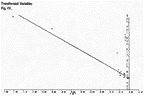
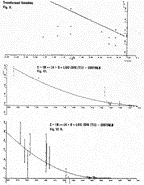
As may be seen from Table 2, the observed values of c lie close to the predicted curve, and when the limits of error are considered nearly all observations fall within the predicted value. The only outstanding exceptions to this are those marked *. One of these (1871) was admittedly an inexact measurement (see Appendix 1). Those from 1932–1940 were all commented upon by Froome & Essen as giving results significantly different from anticipated values (as was 1928). These four exceptions were omitted from the final plot of points. The so-called “Coefficient of Determination,” r2, which is a mathematical expression showing how exactly the curve agrees with the observed points, had a value of one to nine significant figures, indicating a near perfect fit to the data. It is of interest to note that as experimental techniques improved over the 300 years, the difference between the observed and predicted values decreased. All told, 17 values were above the curve and 21 below, the r2 value indicating a perfectly balanced distribution of the cluster of points as well as close proximity to the curve. The total average error is 23.53 km/sec. The total average value is 299,894 km/sec. Thus the average percentage error in the observations is 0.00785%. This compares with a drop in c of 0.5%. Thus the average percentage error is only 1.6% of the total difference in measurement over the last three centuries. It is notable from FigureVI that the error bars show that it is not possible to draw a straight line from the lower limit of the last in the series. This clearly shows that a systematic decay in c has occurred. In addition, from FigureV & FigureVII there are four instances where separate observations in the same year occur with one being above the curve and one below but whose error bars do not reach the curve. This proves that the experimental error estimation in those cases is incorrect and that the curve is therefore more accurate. This should hardly be surprising as a large number of results put together are more likely to give a true total picture than isolated or single experiments. Thus the curve through the set of results has a higher probability of being correct than the individual experiments. In Figures IV & V the curve has been transformed into a straight line and shows the scatter of observed points about this line. Because of the scale in Figure IV the values from 1947 onwards appear as one point with the line going through the center of them. Figure V shows these points on a vastly expanded scale. Thus we can safely conclude that by accepted rules of statistical analysis the probability of the change being due to experimental error is essentially zero.

Answers in Genesis is an apologetics ministry, dedicated to helping Christians defend their faith and proclaim the good news of Jesus Christ.
- Customer Service 800.778.3390
- Available Monday–Friday | 9 AM–5 PM ET
- © 2026 Answers in Genesis