
Chapter 5
Delineation of the Information Concept
Information always plays a substitutionary role. The encoding of reality is a mental process.
The question now arises as to the region in which the derived theorems are valid. Do they only hold for computers or also above and beyond that in all technological domains? Are living systems included or not?
What is the position with regard to unknown systems that we might like to evaluate? Are there criteria which enable us to determine beforehand whether the theorems may be applied, or whether we have left the domain of validity? We, thus, require an unambiguous definition.
We have already considered a number of examples which we have tacitly included in the domain, namely a computer program, a book, flag codes, and hieroglyphics. What about the crystalline structure of a metal or a salt or of a snowflake, all of which become visible under magnification? The starry skies are investigated by means of telescopes and we obtain “information” about the stars in this way. A detective gathers “information” at the scene of a crime and deduces circumstantial evidence from meaningful clues. A paleontologist may observe the mussel-bearing shale in a geological layer. The scientist “studies the book of nature” and obtains new knowledge in this way. New technological regularities are discovered, and, when formulated, they comprise a lot of information. Now, which of the above examples belong to our domain?
Every scientific definition of a concept requires precise formulation, as in everyday communications. A definition serves to fix matters, but it also brings limitations. The same holds for the information concept.
To be able to define a domain, we require a peculiar property of information, namely its representational function. Information itself is never the actual object or fact, neither is it a relationship (event or idea), but the encoded symbols merely represent that which is discussed. Symbols of extremely different nature (see paragraph 4.2) play a substitutionary role with regard to reality or a system of thought. Information is always an abstract representation of something quite different. For example, the symbols in today’s newspaper represent an event which happened yesterday; this event is not contemporaneous, moreover, it might have happened in another country and is not at all present where and when the information is transmitted. The genetic letters in a DNA molecule represent the amino acids which will only be constructed at a later stage for subsequent incorporation into a protein molecule. The words appearing in a novel represent persons and their activities.
We can now formulate two fundamental properties of information:
Property 1: Information is not the thing itself, neither is it a condition, but it is an abstract representation of material realities or conceptual relationships, such as problem formulations, ideas, programs, or algorithms. The representation is in a suitable coding system and the realities could be objects or physical, chemical, or biological conditions. The reality being represented is usually not present at the time and place of the transfer of information, neither can it be observed or measured at that moment.
Property 2: Information always plays a substitutionary role. The encoding of reality is a mental process.
It is again clear from Property 2 that information cannot be a property of matter; it is always an intellectual construct (see Theorems 1 to 3, paragraph 3.3). An intelligent sender who can abstractly encode reality is required.
Both the above salient properties now enable us to delineate the information concept unambiguously. Figure 15 clearly illustrates the domains of information (A) and non-information (B and C). Whenever any reality is observed directly by seeing, hearing, or measuring, then that process falls outside our domain. Whenever a coding system that represents something else is employed, then we are inside our domain A, and then all the mentioned theorems are completely valid as laws of nature. The following basic definition has now been established:
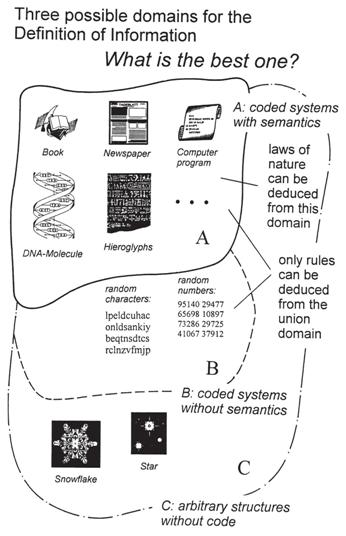
Figure 15: Part A is the domain of definition of information (see Definition D5 for an explanation). In this domain, all the laws of nature about information are valid. The domains B and C fall outside of the definition domain. B represents random characters or random numbers and therefore also lies outside.
Definition D5: The domain A of definition of information includes only systems which encode and represent an abstract description of some object or idea as illustrated in Figure 15. This definition is valid in the case of the given examples (book, newspaper, computer program, DNA molecule, or hieroglyphics), which means that these lie inside the described domain. When a reality is observed directly, this substitutionary and abstract function is absent, and examples like a star, a house, a tree, or a snowflake do not belong to our definition of information (Part B). The proposed theorems are as valid as natural laws inside the domain we have just defined.
It should be noted that the DNA molecule with its genetic information lies inside the domain A. We shall see later that this is a true coding system. Three chemical letters comprise the code for a certain amino acid, but the acid itself is not present, neither spatially nor temporally, as required by Property 1; it is not even present elsewhere. The actual acid is only synthesized at a later stage, according to the code which substitutes for it.
The energy law is valid and exists regardless of our knowledge about it. It only became information after it had been discovered and formulated by means of a coding system (everyday language or formulas). Information, thus, does not exist by itself—it requires cognitive activity to be established.
We can now formulate another information theorem:
Theorem 24: Information requires a material medium for storage.
If one writes some information with chalk on a blackboard, the chalk is the material carrier. If it is wiped off, the total quantity of chalk is still there, but the information has vanished. In this case, the chalk was a suitable material medium, but the essential aspect was the actual arrangement of the particles of the chalk. This arrangement was definitely not random—it had a mental origin. The same information that was written on the blackboard could also have been written on a magnetic diskette. Certain tracks of the diskette then became magnetized, and also in this case there is a carrier for the information as stated by Theorem 24. The quantity of material involved is appreciably less than for the chalk and blackboard, but the amount of material is not crucial. Moreover, the information is independent of the chemical composition of the storage medium. If large neon letter signs are used for displaying the same information, then the amount of material required is increased by several orders of magnitude.
In the Beginning Was Information
Between the covers of this book may well be the most devastating scientific argument against the idea that life could form by natural processes.
Read OnlineRecommended Resources

Answers in Genesis is an apologetics ministry, dedicated to helping Christians defend their faith and proclaim the good news of Jesus Christ.
- Customer Service 800.778.3390
- Available Monday–Friday | 9 AM–5 PM ET
- © 2025 Answers in Genesis


