Energy

A3.1 Energy, a Fundamental Quantity

The concept of energy (Greek energeia = activity) plays such a central role in all of physics as well as in the other natural sciences and in technology, that it is regarded as a fundamental entity, as information is shown to be. In contrast to information, energy belongs to the material world—the lowest level of Figure 14 (chapter 4). Energy appears in numerous forms, many of which can be converted into another form. Many physical processes fundamentally involve nothing else than the conversion of one form of energy into another. The most important forms of energy are:

• mechanical work (energy)
• potential and kinetic energy (energy of rotation and energy of translation)
• the energy of gravitational fields, and of electrical, magnetic, and electromagnetic fields
• heat energy
• electrical energy
• the energy which binds nucleons in atomic nuclei
• chemical energy
• radiation energy of particles (electrons, protons, and neutrons)
• the equivalence of mass and energy

All physical events and processes obey two fundamental principles, known in thermodynamics as the “first law” and the “second law.”

The first law: This important natural law, also known as the “energy law” or the “law of conservation of energy,” was first formulated in 1842 by a German physician, Robert Mayer (1814–1879). It states that energy cannot be created in the observable world, neither can it be destroyed. This law is not an axiom, but is derived from experience as are all natural laws (see Theorem N1, paragraph 2.3). In every chemical or physical process, the total energy of the system and its environment, and thus also the total quantity of energy in the universe, remains constant. It is thus impossible to destroy energy or to add to the total quantity of energy. It can only be converted into other forms. Some important consequences of the energy law are:

• Only events which do not change the total amount of energy, can occur in nature. Walter Gerlach (1889–1979), a German physicist, formulated this principle as follows [R1]: “The law of the conservation of energy plays the role of a police commissioner: it decides beforehand whether a line of thought is acceptable or forbidden.”
• The impossibility of a perpetual motion machine of the first kind: No machine can be constructed which, after being set in motion, can continue working unless the supply of energy is renewed.
• The different kinds of energy correspond quantitatively, and these energy equivalents can be determined empirically.

The second law: The first law is only concerned with the conversion between heat energy and mechanical energy or vice versa, without any regard as to whether the conversion actually takes place or not. The second law, however, determines the direction of the process. By themselves, all processes run in only one direction, i.e., they are irreversible. We know from experience that if a hot block of copper is put in contact with a cold block in an isolated container, heat will be exchanged; the hot block continues to convey heat to the cold one until an average temperature occurs in both blocks. If two blocks at the same temperature are placed in the container, nothing will happen. It does not contradict the first law when one block becomes warmer and the other one cooler, as long as there is no overall loss or gain of heat.

The second law provides us with a criterion for predicting the direction of a given energy process. An abstract though quite meaningful concept—entropy S—is required for a mathematical formulation of this law. Entropy is a quantifiable value which changes whenever heat is converted. In its briefest form, the second law can be expressed as dS ≥ 0 (for closed systems). The following conclusions can then be drawn:

• Entropy cannot be destroyed, but it can be produced.
• It is impossible to construct a periodically functioning machine which does nothing else but deliver useful work by cooling a single reservoir of heat. This means, for example, that the heat content of the sea cannot be used for propelling a ship.
• Heat cannot by itself flow from a cooler body to a warmer one (R. Clausius, 1850).
• It is impossible to build a perpetual motion machine of the second kind: It never happens in nature that an automatic process can let the amount of entropy decrease with no other effect.

The following formulation was first proposed by J. Meixner [M2]: “In the gigantic factory of natural processes, the function of manager is taken over by the production of entropy, because it prescribes the direction and the kinds of the events of the entire industry. The energy principle only plays the role of accountant, being responsible for the balance between what should be and what is.”

The ability of a system to perform useful work: This is an important concept, since work (mechanical effort) can be completely converted into heat. The reverse process, the complete conversion of heat into useful work is theoretically impossible. This asymmetry is a primary result of the second law. In addition, the second law asserts that closed systems tend toward a state where the usable energy is a minimum, and the entropy becomes a maximum. The change in the amount of entropy indicates whether a process is reversible or not. The better a process can prevent an increase in entropy, the more useful energy can be produced. Potential and kinetic energy, as well as electrical energy, can be arbitrarily converted into one another in such a way that the process is very nearly completely reversible and can thus produce a maximum amount of useful work.

On the other hand, heat energy can only be partially converted into mechanical work or into some other form of energy. It is impossible to convert more than a certain fraction of the supplied heat energy, as given by the formula η = (T₂-T₁)/T₂ for an ideal Carnot machine (a reversible Carnot cycle; see also paragraph 2.5). This thermodynamically possible amount of useful energy is known by a distinctive name—exergy. The fact that it is impossible to obtain more work from a heat engine than allowed by η_C follows directly from the second law.

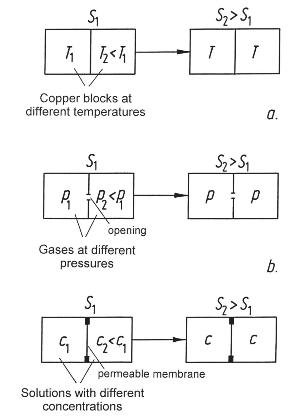
Figure 42: Three processes in closed systems: Two blocks of copper having different temperatures eventually attain the same temperature. If two compartments contain gases at different pressures, the pressures will quickly be equalized through the opening. Two salt solutions having different concentrations exchange their salt content through a permeable membrane. In all three cases, the common aspect is that the entropy of later states is greater than for the initial conditions (S2 > S1).

Living organisms have a greater efficiency (= useful mechanical work obtained from a given energy input) than the maximum thermal efficiency allowed by the second law. This does not contradict this natural law, but indicates that the Creator has endowed body muscles with the capacity to convert chemical energy directly into mechanical work, and do so much more efficiently than ordinary heat engines can.

Conclusion: The law of entropy precludes all events which might lead to a decrease in entropy, even while obeying the energy law. Entropy thus reveals itself to be one of the most important and most remarkable concepts of physics.

Entropy and disorder? In countless publications, examples are given which illustrate that when the entropy of a system increases, the amount of disorder also increases; in other words, the orderliness is diminished. This idea has unfortunately also been extended to biological systems. The following arguments refute such a view:

• Biological processes take place in open systems, and are not closed. The second law allows a decrease in entropy as long as there is a corresponding increase in entropy in the environment. What is completely precluded is that the overall amount of entropy could be diminished.
• There can be no generally valid relationship between entropy and disorder, because entropy is a physical quantity which can be formulated exactly, but there is no exact formulation for disorder. The present author attempted a classification of the order concept in [G5], and different kinds of order are depicted in Figure 43.
• The examples selected for illustrating the apparent relationship between entropy and disorder are, without exception, systems where there is no interaction between components. Such systems are irrelevant as far as biological structures are concerned, since thousands of chemical reactions take place within minute spaces.
• Biological order is based on the information present in all cells. The quality and quantity of this information should now be obvious—see chapter 6 and paragraph A1.2.3.

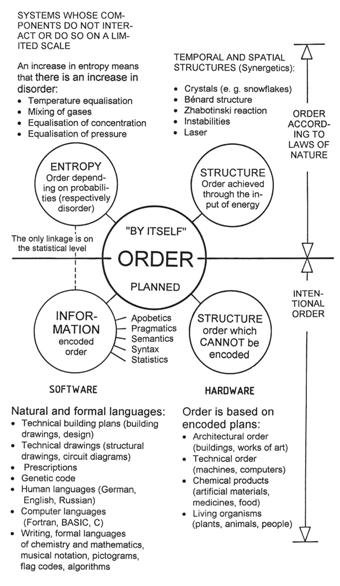
Figure 43: The four kinds of order. The entity “order” which characterizes systems can only be described verbally and not mathematically. We can distinguish between order achieved by means of natural laws. Structures which figure in physical systems can only be maintained as long as the gradients responsible for their existence (e.g., temperature difference), are active. Such an ordering cannot be stored and thus does not refer to a possible evolution. In the lower part of the diagram, ordered systems which are without exception based on some plan are listed. In these cases, information is either involved directly, or there are structures which originated through information.

The ripple patterns produced in beach sand by retreating tides represent a certain order imparted by energetic processes (Figure 44), but there is no underlying code and also no intention. Such order does not represent information and thus cannot be stored.

Figure 44: Ripple marks on beach sand are an example of a structure which originated through the input of energy; this ordering is not based on information (no code is involved).

A3.2 Strategies for Maximizing the Utilization of Energy

The utilization and consumption of energy is always a question of converting one form of energy into another. When the energy produced by a certain source is utilized, the objective is to use the energy as economically as possible. In other words, maximum efficiency is the goal, employing a strategy for maximization. The following sections are devoted to a discussion of technical and biological systems where this principle is used. When energy is consumed, the inverse strategy becomes important, namely minimization of consumption: the available fuel must be used as economically as possible. The required work then has to be done with a minimal input of energy. The brilliant methods and the superlative results achieved by biological systems are discussed in paragraph A3.3.

A3.2.1 Utilization of Energy in Technological Systems

Man’s inventiveness has produced numerous concepts in the field of energy production and utilization. In most cases, the conversion of energy from the primary source to the consumer entails a number of forms of energy. For example, the chemical energy of fuel is converted into heat, the heat is then utilized to produce mechanical work, which, in its turn, is converted into electrical power. In a car engine, the chemical energy of the fuel changes into heat in the combustion chambers, and the explosive expansion of the gases is converted into mechanical work. An electric light bulb converts electrical energy into heat and light. Losses occur during all these conversions, and the ratio between the input energy and the recovered energy represents the efficiency of the process. Even in present-day coal-burning steam generating plants, the efficiency is only about 40%. This means that 60% of the chemical energy of the coal is lost.

In 1993, the total amount of energy generated in Germany was 536.6 TWh [F2, p 1007]. About 5% of this total was water energy, 29.6% was obtained from nuclear reactions, and the rest was generated by the combustion of fossil and other fuels (coal and lignite 55.4%, plus natural gas, oil, and diverse other sources). With the exception of the limited hydro-electrical sources, all these processes involve heat conversion with its low efficiency.

Great technological efforts are exerted to achieve direct conversion of energy without any intermediate forms. Examples include fuel cells, magnetohydrodynamic generators, and photo-voltaic elements. The efficiency of the latter is only about 10%, and the others are not yet technologically viable.

Even in the sunny southern regions of Europe, solar power installations, employing concave mirrors to generate steam (which then drives turbines for the production of electricity), require a total mirror surface of 26,000 m² (2.5 football fields) to generate 1 GWh per annum [X1]. This amounts to one million kilowatt-hours per year—enough to supply 350 homes. It would require an enormous area of 42 square miles (68 square km) to generate the same quantity of electricity as that which can be produced by one 1,300 megawatt nuclear power plant. This area could accommodate 150,000 urban inhabitants.

Wind-driven power plants also require a lot of space. It would require 800 to 900 windmill towers of 492 feet (150 m) to equal the energy production of one 1,300 megawatt nuclear plant. Four chains of such windmills separated by a distance of 1,312 feet (400 m) would extend over a distance of 50 miles (80 km).

A3.2.2 Utilization of Energy in Biological Systems (Photosynthesis)

Photosynthesis is the only natural process by means of which large quantities of solar energy can be stored. Requiring only carbon dioxide (CO₂), water (H₂O), and small quantities of certain minerals, it is the fundamental process for supplying the energy which plants need for growth and reproduction. The organic substances produced by plants are the primary source of nutrition and energy for all heterotrophic1 organisms which cannot utilize photosynthesis directly. It can truthfully be stated that photosynthesis is the primary source of energy for all life processes and it also provides most of the usable energy on earth. All fossil fuels and raw materials like coal, lignite, crude oil, and natural gas have been derived from the biomass of earlier times which was formed by photosynthesis.

This process synthesizes complex, energy-rich substances. What usually happens in oxidation/reduction reactions is that a strong oxidizing agent oxidizes a reducing substance, but photosynthesis is exceptional in this respect. It employs a weak oxidizing substance (CO₂) to oxidize a weak reducing agent (H₂O) to produce a strong oxidizing substance (O₂) and a strong reducing compound (carbohydrate). This process requires the input of external energy, namely sunlight. Such a process can only occur in the presence of a substance which can absorb light quanta, transfer the energy to other molecules, and then revert to its initial state where it can again absorb quanta of light. Chlorophyll performs this complex function. There are five types of chlorophyll (a, b, c, d, and f ), which differ only slightly in chemical structure. Occurring in “higher” plants and in green algae, types a and b are the most important. The chemical equation for photosynthesis is:

6 CO₂ + 6 H₂O + light energy → C₆H₁₂O₆+ 6 O₂ (1)

In this process, glucose is synthesized from CO₂ and H₂O by employing the energy of sunlight. The capture of light energy and its conversion to chemical energy is only one part of the process. These initial reactions are called photochemical reactions, and all subsequent reactions where chemical energy is utilized for the synthesis of glucose do not require light energy; they are thus known as dark or umbral reactions.

The ability to absorb light varies very strongly from one substance to another. Water absorbs very little light and thus appears to be colorless. The color of a substance depends on the absorption (and reflection) of certain wavelengths of light. When the degree of absorption is plotted against wavelength, we obtain an absorption spectrum. Chlorophyll only absorbs blue light (wavelength 400 to 450 nm) and red light (640–660 nm), so that the reflected light is green. The active spectrum of a process refers to its efficiency in relation to its wavelength. It is therefore noteworthy that the absorption spectrum of chlorophyll closely corresponds to the active spectrum of photosynthesis. This indicates that a finely tuned concept underlies this vital process and an efficiency calculation supports the view that a brilliant mind is involved.

The efficiency of photosynthesis: According to equation (1), exactly 1 mol2 of glucose is generated from 6 mol CO₂ [1] requiring an energy input of 2,872.1 kJ. For 1 mol of CO₂, this amounts to 478.7 kJ. As a loss of energy is inherent in each and every energy conversion, the actual quantity of light energy required is greater. Although red light quanta possess less energy (about 2 eV/light quantum) than blue light quanta (approximately 3 eV/quantum), due to different efficiency both types produce approximately the same amount of photochemical work. It has been determined experimentally that 8 to 10 light quanta are required for every molecule of CO₂. The energy content of 1 mol of red light quanta (= 6.022 x 10²³ quanta [2]3) amounts to 171.7 kJ. Therefore, 9 mol of red light quanta (the average of 8 and 10) is found by multiplying 171.7 kJ x 9. The result is 1,545.3 kJ. The efficiency Ë can be calculated as the ratio between the theoretical amount of energy required to assimilate 1 mol CO₂ (478.7 kJ) and the actual energy content of the incident red light (1545.3 kJ):

η_red = 478.7/1,545.3 x 100% = 31%

The energy content of blue light quanta is 272.1 kJ/mol, so it follows that η_blue = 20%.

Volume of photosynthesis: The productivity of plants is not only qualitatively but also quantitatively highly impressive. A single beech tree which is 115 years old has 200,000 leaves which contain 180 grams of chlorophyll and have a total area of 1,200 m², and can synthesize 12 kg of carbohydrates on a sunny day, consuming 9,400 liters of CO² from a total volume of 36,000 m³ of air [S4]. Through the simultaneous production of 9,400 liters of oxygen, 45,000 liters of air are “regenerated”! On a worldwide scale, 2 x 10¹¹ tons of biomass is produced annually by means of photosynthesis [F6]. The heat value of this mass is about 10¹⁴ watt-years (= 3.15 x 10²¹ Ws). The entire human population annually consumes about 0.4 TWa = 1.26 x 10¹⁹ Ws (1 TWa = 1 Terawatt-year = 3.1536 x 10¹⁹ Ws), and all the animals require 0.6 TWa. Together, these add up to only one percent of the total annual biomass production.

Respiration: The result of breathing, namely the release of energy, is the opposite of photosynthesis. These two processes are in ecological equilibrium, so that the composition of the atmosphere stays constant, unless it is disturbed by human intervention like heavy industries. It should also be noted that the mechanisms for photosynthesis and respiration are astoundingly similar. The substances involved belong to the same chemical classes. For example, a chlorophyll molecule consists of four pyrrole rings arranged round a central atom, which is magnesium in the case of chlorophyll, and iron in the case of hemoglobin, the active substance on which respiration is based. Both processes occur at the interface of permeable lipid membranes. The inevitable conclusion is that a single brilliant concept underlies both processes and that both are finely tuned to each other. We can thus reject an evolutionary origin, since two such astonishingly perfect and similar processes could not possibly have originated by chance in such diverse organisms.

Conclusion: It has not yet been possible to explain the incredible complexity of the molecular mechanisms on which photosynthesis is based. The same situation holds for respiration. The fact that the chemical equations and some of the intermediate enzyme driven steps are known should not create the impression that these processes are really understood; on the contrary, what we don’t yet know is incomparably more than what we do know. The American biophysicist Albert L. Lehniger [L1] regards these unresolved questions as some of the most fascinating biological problems. All solar energy engineers dream of devising a process which can convert sunlight directly into fuel. Although photosynthesis takes place in every single green leaf of all plants, having been conceived in an astoundingly brilliant way, even the most inventive engineer is unable to imitate the process. Every phototropic cell is supplied with the information required to undertake such an optimal energy conversion process.

A3.3 The Consumption of Energy in Biological Systems: Strategies for Minimization

Every cell requires energy continuously for its vital functions like the synthesis of new molecules, or the production of a daughter cell. In multicellular organisms there are further purposeful reactions (e.g., locomotion, and the control of body temperature). The conversion of energy in every cell, whether animal, vegetable, or microbial, is based on the same principles and mechanisms. In contrast to technological practices, living organisms avoid the inefficient use of heat as an intermediate energy form. Cellular processes are isothermic; this means that the temperature does not change.

The concept of energy: It should be emphasized that the energycarrying nutrient molecules do not generate heat when they are oxidized. The molecular concept of biological oxidation involves numerous precisely tuned individual catalytic enzyme reactions which follow one another in exactly the required sequence, and employ just as many intermediate compounds. Adenosin triphosphate (ATP) has some special chemical properties which enable it to perform important functions. It belongs to the group of nucleotides, comprising adenine, C5-sugar, D-ribose, and phosphate groups. When nutrients are oxidized to generate energy, the more energy-rich ATP is formed from adenosin diphosphate (ADP). The energy stored in ATP can then subsequently be utilized by conversion into chemical work (e.g., biosynthesis), mechanical actions (e.g., muscular effort), or osmotic transportation. When this happens, the ATP loses one phosphate group, and reverts to ADP. In this energy transfer system, ATP is thus the charged substance, and the ADP is neutral. The numerous very complex intermediate chemical steps in this ATP/ADP energy cycle are catalyzed by a specific set of enzymes. In addition to this general flow of biological energy, there are some very clever special mechanisms for energy conversion.

Certain fishes like the electric eel can generate electrical pulses of several hundred volts directly from chemical energy. Similarly, light flashes emitted by some animals and organisms represent converted chemical energy. The bombardier beetle converts the chemical energy contained in hydrogen peroxide into explosive pressure and volume changes.

Machines constructed for the purpose of energy utilization essentially involve the generation of easily transportable electrical energy in a round-about way by first producing heat. Heat Q can only perform useful work W when there is a temperature difference T₂-T₁. The theoretical maximum amount of work that can be performed by a heat engine, is given by the Carnot formula:

W = Q x (T₂-T₁)/T₂

T₂ can be the initial temperature of the steam entering a turbine, for example, and T₁ can be the exhaust temperature. It follows that large temperature differences are required to produce a reasonable amount of useful work. In living cells, the processes for generating energy must be fundamentally different, since all reactions have to take place at the temperature of the cell; in other words, the processes must be isothermic. The refined energy concepts realized in cells utilize substances which are unstable to heating, but still achieve exceptionally high degrees of efficiency.

The cells: A living cell can be compared with a factory comprising several departments, each of which has a certain number of machines.

The work of all the cell’s departments and machines involves optimally geared interrelationships exhibiting planning down to the last detail. The end products are produced through a coordinated sequence of numerous individual processes. We can rightly state that we are dealing with the smallest fully automated production line in the world; it even has its own computer center and its own power generating plants (the mitochondria). With their diameter of 100 nm, the prokaryotes are the smallest cells, while birds’ eggs are the largest. Ostrich eggs measure about 0.1 m = 10⁸ nm, and the average radius of the cells of multicellular organisms lies between 2,000 nm and 20,000 nm (= 2 to 20 μm). Large living beings consist of tremendously large numbers of cells (about 10¹⁴ for humans), while the smallest organisms like bacteria are unicellular. Two large classes of cells are distinguished according to their structural organization, namely prokaryotic cells (Greek karyon = nucleus) and eukaryotic cells (Greek eu = good). Many unicellular organisms like yeast cells, protozoa, and some algae, are eukaryotic, as well as nearly all multicellular forms. Their cells contain a nucleus, mitochondria, and an endoplasmic reticulum. The prokaryotes comprise the bacteria and the blue algae. Compared to the eukaryotes, they are considerably smaller (only 1/5,000th in volume), less differentiated and less specialized, and they lack many of the structures like a nucleus or mitochondria.

Summary: We can now summarize the essential characteristics of energy utilization by organisms, which is fundamentally different from technological processes:

1. Isothermic energy conversion: Energy processes take place at a constant temperature (they are isothermic); pressures and volumes are also constant. The roundabout and inefficient technological methods which depend on the generation of heat are circumvented.

2. The greatest possible miniaturization: One of the aims of technology, the miniaturization of equipment, is realized in cells in a way that cannot be imitated. The energy generating and consuming processes in an organism are coupled at the molecular level. We can rightly speak of “molecular machines,” representing the ultimate in miniaturization.

3. Optimal operation: Each and every one of the approximately ten thousand milliard (10¹³) muscular cells in the human body possesses its own decentralized “power generating plant.” These can become operational as and when required, and are extremely economical as far as the transfer of energy is concerned.

4. The indirect conversion of energy: Energy is not applied directly, but the ATP system acts as a transfer medium from the energygenerating process to the reaction consuming energy. It should be noted that ATP, a substance of high energy content, is not used for storing energy, only to transfer it. The ATP-driven, energy-consuming processes can be of a very diverse nature: mechanical work is performed in contracting muscles; electrical energy is set free in the respective organs of some animals; when substances are absorbed or transported osmotic work is done, and in many cases the result is chemical work. All of these processes are included in an extensive metabolic chain effected by an extremely complex and often incompletely understood enzyme system.

5. High efficiency: Compared to fermentation (from glucose to lactic acid), respiration (from glucose to CO₂ and H₂O) is an extremely efficient process, releasing all the energy stored in glucose molecules. The efficiency of the transportation of electrons in this case is 91%, a ratio which engineers can only dream of. This fascinating process occurs in a brilliantly constructed system which continuously employs the “principle of a common intermediate product for the transfer of energy.” ATP is the link between reactions which supply energy and those which require energy; in other words, cells have an energy exchange unit which is readily convertible. The processes which release energy provide the “currency” which is then spent by those processes requiring energy. The ATP system channels the transfer of energy, providing the cell with excellent control over the flow of energy.

The biological energy conversion system is so brilliantly and cleverly designed that energy engineers can only watch, fascinated. Nobody has yet been able to copy this highly miniaturized and extremely efficient mechanism.

A3.4 Conservation of Energy in Biological Systems

In regard to the relationship between physics and biology, Alfred Gierer, a physicist of Tübingen (Germany), concluded [G1]: “Physics is the most general science since it can be applied to all events in space and time, while biology is the most complex science which involves ourselves to a large extent.” Some important questions now arise: Are there any processes occurring in living organisms where physical and chemical laws do not apply? Does a living organism differ fundamentally from a machine or not? Could biology be based on physics? Two aspects should be considered very carefully before we can answer such questions, namely:

1. Course of events: All biological processes strictly obey physical and chemical laws (see Theorems N2, N3, and N4 in paragraph 2.3). These laws, however, only delineate the external framework within which the relevant events generally occur. The environment imposes additional constraints. Furthermore, the inherent operational information (see chapter 11 for a definition) underlies all functions of living organisms. All these mostly very complex processes are program controlled.

2. Origin: Just as each and every machine, from a simple corkscrew to a computer, cannot be explained in terms of natural laws and environmental conditions only, so also does every biological system require an inventor, a constructor, a source of ideas. Every creator of a technological invention must know the laws of physics; he employs these laws to construct a suitable mechanism. Although the laws impose constraints, they also provide conditions which can be utilized. He displays his ingenuity when, by using constructional and architectural ideas, he constructs a machine which employs the natural laws in such a way that it is obviously an optimal solution. The same holds for the Creator of biological systems. How much more is His wealth of ideas and His unfathomable wisdom reflected in living systems!

Physical laws can describe and delineate the progress of biological processes, but they fail to explain their complexity and the wealth of their structures and functions. Anybody who discusses questions of origin and of spirituality on a purely material plane removes himself completely from the realities of life by such a mechanistic reduction.

The following examples of energy conservation illustrate the immeasurable inventiveness of the Creator. In many cases, the laws of nature are employed right up to the limits of what is physically possible.

A3.4.1 Animal “Chlorophyll”

Photosynthesis has now been recognized as a brilliant invention for the conversion of the energy of the sun to produce energy donors. There are three kinds of animal [D4] which have a similar “built-in” capacity, namely the snail Tridachia crispata, the three-millimeter spiral worm Convoluta roscoffensis which lives on the coast of Normandy and Bretagne, and the microscopic green Paramecium bursaria.

The tridachia snails are found in the waters around Jamaica and they normally subsist on seaweed, but when seaweed is not available, they can still survive. Chlorophyll eaten previously is not fully digested, but some of it is stored in the form of undamaged chloroplasts in leaf-shaped tufts on its back. These floral organelles are still functionally active and produce sugar when exposed to sunlight. This sugar is then distributed through its body to provide energy. It can now be stated that:

• The animal borrows the chemical factory of the plant, including its control information, and thus virtually changes itself into a plant.
• This snail ingests seaweed which then ensures sufficient nutrition for up to six weeks when exposed to sunlight. This is an amazing principle.

All human nutritional problems could be solved if only we could imitate these animals. Photosynthesis is such a brilliant informationcontrolled process that it is not really understood; it is also impossible to copy it chemotechnically. It has not yet been possible to imitate the above mentioned animals by utilizing and preserving chloroplasts (the chlorophyll organelles) with their functions intact, outside of leaf cells.

A3.4.2 Animals with “Lamps”

As far as energy is concerned, there is another extremely interesting phenomenon exhibited by many sea animals and some simple land animals (e.g., glowworms; see details in [G15]), namely bioluminescence (Latin lumen = light). These organisms can emit light of various colors (red, yellow, green, blue, or violet) and in different signal sequences. When technological light production is compared to bioluminescence, the former proves to be extremely inefficient as far as energy input is concerned. Normally, an electric light bulb only converts 3 to 4 percent of the applied energy into light, and the efficiency of a fluorescent tube is only about 10%. Our lamps could be considered to be heat generators rather than radiators of light.

Bioluminescence, being an invention of the Creator, involves the radiation of cold light—a reaction which no man has yet been able to copy. In this process, certain illuminative substances (luciferin) are oxidized by an enzyme called luciferase. Three fundamentally different types of luciferin can be distinguished, namely that of bacteria, that of fireflies, and that of the Cypridina. An American biochemist, professor W.D. McElroy, was able to quantify the efficiency of this type of light production. It was found that each and every quantum of energy transported to the light organ in the form of ATP4 was converted to light. The number of oxidized luciferin molecules is exactly equal to the number of emitted light quanta. All the light emitted by a firefly is “cold” light, which means that there is no loss of energy through the radiation of heat. We are thus dealing with lamps which are 100% efficient because of the complete conversion of energy into light.

Many bacteria, tiny organisms, insects, and deep sea fishes especially, have been equipped with this method of producing light by the Creator. The best-known examples are the fireflies and the glowworms (Lampyris and Phausis). Most of the subtropical and tropical lampyrids can emit deliberate sequences of flashes; the European ones are not able to do this. In experiments with the black firefly (Photinus pyralis) it was found that the flying male emitted 0.06 second flashes at intervals of 5.7 seconds, and the female on the ground replied after exactly 2.1 seconds with the same rhythm.

These flashing signals are obviously understood by the prospective mate. There also are insects that have lamps which emit different colors, like the Brazilian train worm (Phrixothrix). This beetle larva (Driliden) which lives on snails, normally carries two orange-red lights in front. At the approach of danger, two sets of 11 greenish lanterns are switched on, one on each side. This resembles a train, and the name “train worm” is quite apt.

During a visit to Israel in 1985, we went to the underwater observatory in Eilath and could watch the lantern fish (Photoblepharon palpebratus steinitzi) living in the Red Sea. This fish does not produce its own light, but obtains it from symbiotic luminescent bacteria. These bacteria are so small that the light of a single one is invisible, but the light of an entire colony can be observed. They congregate on an oval light organ situated below the eyes of the fish and are fed and provided with oxygen through a densely branching network of capillary blood vessels. They continuously generate light, but the fish can deliberately switch the light on and off. It does this by pulling a black skin flap over the luminescent organ like an eyelid, and is thus able to transmit different flashing signals. These signals attract the prey it requires for subsistence.

Bacterial emission of light is fundamentally different from that of other luminescent organisms. Other marine organisms only emit light when they are disturbed or stimulated (e.g., by the passage of a ship or of a mackerel school, or the breaking of waves), but bacteria continuously emit light of a constant intensity.

The bioluminescence of abyssal creatures, like glowing fishes, crabs, arrow worms, and jellyfishes, is quite impressive. Many kinds of fish have lamps along their sides, while others have several rows of lamps. The luminous organs can be arranged in curves, in oscillatory patterns, or quite irregularly. The five-striped star constellation fish (Bathysidus pentagrammus) has five beautiful shining lines on both sides of its body, each of which consists of a row of large pale yellow lights, surrounded by serrated bright purple “jewels.”

Luminous shrimps (Sergestes prehensilis) have more than 150 light points, all of which can be quickly switched on and off. For one or two seconds yellow-green lights flash sequentially and quickly from head to tail, just like neon advertisements in cities. Many kinds of fish employ luminescent bacteria to generate light flashes, but others have highly specialized organs which produce their own luminous substances. Some fishes have intricately constructed light projectors, concentrating lenses, or other optical equipment which can, for example, direct a ray of light in a specific direction. The projectors are constructed in such a way that a mosaic of thousands of minute crystals acts as a perfect mirror behind the luminous tissues. Some creatures even have color filters (pigment membranes) for producing any shade of color.

The inventiveness of the Creator is infinite, and we can only stand amazed.

A3.4.3 The Lung, an Optimal Structure

As in the case of biological systems, the construction of an efficient technological plant requires that the consumption of energy should be a minimum. One should pay special attention to irreversible processes, since they determine the cost of the energy. In flow processes, friction is the decisive irreversible factor. Frictional losses can be reduced by having large diameter conduits and by decreasing the contact areas. There are constraints: the provision of generous dimensions in a processing plant increases investment costs considerably, and in living organisms much more basic energy would be required. The total quantity of energy required by an organ or a muscle consists of two parts, namely a certain minimum which is necessary for proper functioning, plus any increase needed for greater activity.

Continuing the work of Swiss physiologist and Nobel Laureate Walter R. Hess (1881), and using the human lung as an example, E.R. Weibel [W2] showed that this optimization problem is solved in a remarkable way. The lung is constructed in such a fashion that when the body tissues are relatively inactive and thus require a minimum of input material and energy, then only a small increase in the basic conversion process is involved to overcome pressure losses. The air passage branches into the well-known two bronchi, each of which again branches into two smaller passages having equal diameters. This pairwise furcation into smaller conduits continues until the 23rd level, which represents the finest air capillaries. The average ratio d₂/d₁ of two consecutive diameters (d₂ following d₁) is very nearly 0.8. When pressure decreases have to be a minimum for a given volume of conduits and laminar flow must be maintained, then the result obtained by optimization calculations in fluid dynamics is found to be d₂/d₁ = (1/2)^1/3 = 0.79370. This is consistent with the measured value of 0.8 and this (1/2)^1/3 formula holds even more exactly for the furcations of the blood vessels supplying the lung. The more we study the details of biological systems, the stronger the impression becomes that their Creator is a brilliant constructor and inventor.

A3.4.4 The Flight of Migrating Birds

The flight of birds is one of the most fascinating kinds of propulsion seen in creation. It involves numerous solutions which cannot be imitated technologically [D2, R3, and S2]. Aerodynamically, birds’ wings are highly specialized and optimized structures. Their curvature is especially important, otherwise they could not fly. An airplane has to have a fairly high minimum airspeed to stay airborne, but birds can utilize the updraught caused by their wing strokes to fly quite slowly. Their wings are carrier surfaces as well as propellers; the efficiency of the latter function is very high, and cannot yet be attained by technological means. We now discuss two of the numerous problems solved in the design of bird flight, namely the matters of precise energy calculations and exact navigation.

A3.4.4.1 The Flight of Migrating Birds: An Accurate Energy Calculation

Every physical, technological, and biological process strictly obeys the energy law, namely that a certain total amount of energy is required. Migrating birds have to carry enough energy in the form of fat to complete their journey, but birds’ bodies have to be as light as possible, so unnecessary weight should be strictly avoided. It is also necessary that fuel consumption should be optimal. How did the Creator provide for enough fuel without having “reserve tanks” or overnight “pit stops”? The first aspect is to determine the most optimal speed. If a bird flies too slowly, it consumes too much fuel for propulsion. If it flies too fast, then more energy is required to overcome air friction. There is thus a certain optimum speed for minimum fuel consumption. If the bird knew this special speed, it could fly the most economically. Depending on the aerodynamics of its body and its wings, every bird has a specific optimal speed (it is 45 km/h in the case of the Aztec seagull, for example; and 41.6 km/h for a parakeet). It is known that birds keep exactly to their optimum energy-saving speed when traveling. How do they know this? It is just one of many puzzles which ornithologists cannot solve.

We now consider the energy problem in more detail in the case of the golden plover (Pluvialis dominica fulva). These birds migrate from Alaska to spend the northern winter in Hawaii. They have to fly non-stop over the ocean without resting, because there are no islands en route, neither do they swim. During this 88-hour journey of more than 2,485 miles (4,000 km) (depending on the point of departure), they beat their wings an enormous 250,000 times without stopping at all. At the start, their average weight G₀ is 200 g, 70 g of which is padding (fat) which serves as fuel. It has been found that these birds consume 0.6% of their weight per hour (fuel consumption p = 0.006/h) to produce propulsion energy and heat. During the first hour the amount of fuel x₁ it thus requires

x₁= G₀ x p = 200 x 0.006 = 1.2 g fat. (1)

At the beginning of the second hour it weighs G₀-x₁ = 200 - 1.2 = 198.8 g, so that it consumes somewhat less energy during the second hour:

x₂= (G₀-x₁) x p = G₁ x p = 198.8 x 0.006 = 1.193 g (2)

x₃= (G₀-x₁-x₂) x p = G₂ x p = 197.6 x 0.006 = 1.186 g (3)

For the 88th hour the fuel consumption is down to

x₈₈ = (G₀-x₁-x₂-x₃-… -x₈₇) x p = G₈₇ x p (4)

because of its reduced weight. We can now calculate its weight at the end of the journey, after subtracting the hourly weight reduction:

1st hour: G₁= G₀-x₁= G₀-G₀ x p = G₀(1-p) (5)

2nd hour: G₂= G₁-x₂= G₁-G₁ x p = G₁(1-p) = G₀(1-p)² (6)

3rd hour: G₃= G₂-x₃= G₂-G₂ x p = G₂(1-p) = G₀(1-p)³ (7)

zth hour: G_z= G_z-1-x_z= G_z-1-G_z-1 x p = G_z-1(1-p) = G₀(1-p)^z (8)

88th hour: G₈₈= G₈₇-x₈₈= G₈₇-G₈₇ x p = G₈₇(1-p) = G₀(1-p)⁸⁸ (9)

The hourly weights G₀, G₁, . . . , G₈₈ form a geometric sequence with common ratio q = 1 -p < 1. This computation is somewhat oversimplified,5 but, by substitution in (9) we find the final weight after 88 hours to be:

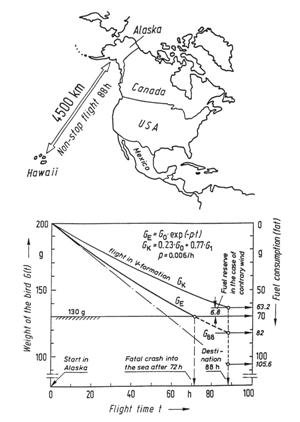
Figure 45: The flight of the East Siberian golden plover. For the migration of up to 4,500 km from Alaska to Hawaii, the amount of available fuel is 70 g. If this flight is undertaken by a single bird, it would consume all its fat reserves after 72 hours and would plunge into the ocean 800 km from its destination. On the other hand, flying in a V formation reduces the energy consumption by 23%, so that the birds reach their destination safely.

G₈₈ = 200 x (1 - 0.006)⁸⁸ = 117.8 g (10)

The total fuel consumption is given by

G₀-G₈₈ = 200 - 117.8 = 82.2 g (11)

G_z= G₀ x (1-p)^z = 200 - 70 = 130 g.

which is appreciably greater than the 70 g of fat the bird started out with! The bird’s weight cannot go below 130 g (see Figure 45). In spite of flying at the optimum speed for minimal fuel consumption, the bird would not be able to reach Hawaii because it started out with too little fat. To determine the number of hours that the bird could fly with the given amount of fuel, we have to solve the following equation for z:

The result is that the 70 g of fat will be consumed after 72 hours, which is 81% of the required flying time. This means that the bird would plunge into the ocean about 497 miles (800 km) short of its destination. Did we make some mistake, or has the bird been inadequately constructed by the Creator? The answer to both questions is “no.” We regard the Creator’s work with amazement. He employs the fundamental theorem which states that “energy input is optimized through information.” In the case of the plover, this means that the bird has been given some important additional information, namely: “Do not fly alone (curve G_A), but fly in a V formation (curve G_V)! In the V formation, you will save 23% of your energy and will then safely reach your destination.” Curve G_V in Figure 45 depicts the weight decrease in V formation. After 88 hours, the normal residual amount of fat is 6.8 g, which has not been carried along unnecessarily, but is a reserve to be used when head winds are encountered. The extremely low specific rate of fuel consumption, p = 0.6% of its weight per hour, is all the more amazing when we compare it with that of man-made aircraft which is many orders of magnitude greater (for a helicopter p = 4 to 5%; and p = 12% for a jet plane).

Somebody who does not regard these precise phenomena as the work of the Creator cannot answer the following questions:

• How does the bird know the exact energy requirement?
• How is it possible that the bird accumulates the exact amount of fat before the journey?
• How does the bird know the distance and the specific fuel consumption?
• How does the bird know the migration route?
• How does the bird navigate to reach its destination promptly?
• How does the bird know to fly in a V formation with other birds to reduce fuel consumption?

In my book If Animals Could Talk [G15], the golden plover acts as narrator involving the reader in an imaginary dialogue. The facts presented here are used as point of departure to draw the reader’s attention to numerous wonders of creation.

Besides the Eastern Siberian golden plover mentioned above, there is also the North American golden plover (Nominatrasse). These birds also undertake a non-stop long distance migration flight from the coast of Labrador across the Atlantic Ocean to Brazil. The western plovers follow the same route for both the outward and the return journey, but the American plovers use different routes in autumn and spring. On the northward leg, they fly back to Canada over Central America and the United States. Some further astonishing migration feats are:

• —The Japanese snipe (Capella hardtwickii) flies 5,000 km to Tasmania.
• The East Siberian spine-tailed swift (Chaetura caudacuta) migrates from Siberia to Tasmania.
• The migration route of the American sandpipers (e.g., Calidris melanotus = grey breasted sandpiper) covers 16,000 km from Alaska to Tierra del Fuego at the southern tip of South America.

A3.4.4.2 The Flight of Migrating Birds: A Navigational Masterpiece

Finn Salomonsen, a Danish ornithologist, writes the following about the in-flight orientation of birds [S2]: “The ability of birds to find their way while flying is a mystery and a puzzle. Few other questions have over the years given rise to so many theories and speculations as this one.” This navigational ability is indeed a supreme wonder, since birds do not have complex gyroscopes, compasses, or maps, and environmental conditions like the position of the sun, wind direction, cloud cover, and day-night rhythms, keep changing all the time. When terrestrial birds have to cross an ocean, as we have seen in the case of the golden plover, a small error in direction would result in their floundering helplessly over the open ocean and finally plunging to their death. Setting an exact course is not a question of trial and error, because a large majority of the migratory birds would never reach their destination without exact navigation. No species could survive such great losses. Any evolutionistic view of this fact can be rejected out of hand. The idea that juvenile birds are shown the way by their parents plays a minor role at most, since many kinds of birds fly singly. We thus have to assume that migratory birds possess an inherent sense of direction which enables them to orient themselves with respect to geographical direction and to stay on course. This sense of direction is demonstrated by Salomonsen in the case of two kinds of small birds living in western Greenland and which both migrate to the south in autumn. The wheatear (Oenanthe oenanthe) and the snow canary live in the same region, and they often begin their migration at the same time, but their ways part after arriving in southern Greenland. The snow canaries continue directly south to spend the winter in America, while the others turn southeast and fly right across the Atlantic Ocean to western Europe and North Africa. Both kinds of bird have a specific sense of direction which determines their different courses.

Detailed results about navigational precision have been found by transporting different kinds of birds to distant locations. A noteworthy experiment was undertaken with two kinds of marine swallows (Sterna fuscata and Anous stolidus) which breed on the Tortugas Islands in the Gulf of Mexico. The birds were taken by ship in different directions and were released at distances of between 517 and 850 miles (832 and 1368 km) from their nesting place. Although they found themselves in, for them, unknown parts of the ocean, most of them returned home after a few days, flying unswervingly straight back to their eggs and their young on the Tortugas Islands.

Many experiments have been carried out with homing pigeons, and their navigational abilities have been extensively investigated and described. Salomonsen writes as follows about these breathtaking marvels of navigation [S2]:

Even when pigeons have been transported while anaesthetized, or when their cage was rotated so that its orientation changed continuously, they were able to fly back home just as readily as undisturbed pigeons, when released. It can be asserted without a doubt that these birds possess a special ability for determining their geographic position; they have a real navigational sense. We know nothing about the actual nature of this sense, neither do we know where the special sense organ is located.

These birds have exceptional faculties: They can return home over great distances, even though deprived of any possibility of orientation when transported. Wherever they are released, they have the amazing ability to extract the required data from the environment to determine their position relative to their home. Even after having oriented themselves in this unknown way, the real problem arises, namely en route navigation. A simple sense of direction is inadequate for this purpose.

When crossing oceans, the birds have to take drift, caused by the perennial winds, into consideration. To avoid wasting energy on detours, such factors have to be determined and corrected continuously, as with a cybernetic control system. The Creator provided birds with a very precise “autopilot” which is obviously able to monitor environmental data continuously and compare it with the internally programmed home location and the envisioned geographic destination, to guarantee the quickest and most economical route. As yet, nobody but the Creator who devised it knows the location of this vitally important system, neither do we know how the operational information is encoded. We use a special term to cover our ignorance; we say the birds have “instinct.”