
Chapter 2
Principles of Laws of Nature
Through the natural sciences, the world around us is observed for the purpose of discovering the rules governing it.
2.1 The Terminology Used in the Natural Sciences
Through the natural sciences, the world around us is observed for the purpose of discovering the rules governing it. Experimentation and observation (e.g., measuring and weighing) are the basic “modus operandi.” Hans Sachsse, who specialized in natural philosophy and chemistry, described (natural) science as “a census of observational relationships which cannot say anything about first causes or the reasons for things being as they are; it can only establish the regularity of the relationships.” The observational material is organized systematically, and the principles derived from it are formulated in the most general terms possible (e.g., construction of machines). Questions about the origin of the world and of life, as well as ethical questions, fall outside the scope of science, and such questions cannot be answered scientifically. Conclusions about matters that do fall within the scope of (natural) science can be formulated with varying degrees of certainty. The certainty or uncertainty of the results can be expressed in various ways.
Law of Nature:
If the truth of a statement is verified repeatedly in a reproducible way so that it is regarded as generally valid, then we have a natural law. The structures and phenomena encountered in the real world can be described in terms of the laws of nature in the form of principles which are universally valid. This holds for both their chronological development and their internal structural relationships. The laws of nature describe those phenomena, events and results which occur in the interplay between matter and energy. For these reasons, psychological emotions like love, mourning, or joy, and philosophical questions are excluded from the natural sciences. Statements about natural events can be classified according to the degree of certainty, namely: models, theories, hypotheses, paradigms, speculations, and fiction. These categories are now discussed.
Model:
Models are representations of reality. Only the most important properties are reflected, and minor or unrecognized aspects are not covered. Models are important because of their illustrativeness. A model is a deliberate but simplified representation of reality, and it describes observed structures in a readily understandable way. It is possible to have more than one model for a given reality, and, because it is by nature provisional and simple, any model can always be improved upon.
Theory (Greek theoría = view, consideration, investigation):
Theories endeavor to explain facts in a unified representation of models and hypotheses. To put it briefly, a theory is a scientific statement based on empirical findings. Since empirical results are seldom final, theories are of a provisional nature, and the inherent hypothetical element inevitably causes uncertainty—in the best case, a statement can be made in terms of specific probabilities. Theories are therefore a means of tying observed facts together, and the best theories are those which attain this objective with the least number of inconsistencies.
Hypothesis (Greek hypóthesis = assumption, conjecture, supposition):
A hypothesis is an unverified scientific conjecture which contains speculations and which amplifies an incomplete empirical result or provisionally explains some fact. Any new hypothesis must be based on facts, and it may not contradict the known laws of nature. If a hypothesis serves as a methodological guide when a new research project is undertaken, it is known as a working hypothesis. When observational facts support a hypothesis, the probability of its being true is increased, but if one contradicting fact is uncovered, the hypothesis must be rejected (falsification). As early as the 17th century, Blaise Pascal (1623–1662) said that we could be certain that a hypothesis is false if one single derived relationship contradicts any observed phenomenon.
Paradigm (Greek parádeigma = example, sample):
When a certain theory (or a system of hypotheses, or a worldview) pervades entire fields of research or an entire scientific era, it is known as a paradigm. Such a view then dictates the scope for specific researches and delineates the presuppositions used for explaining individual phenomena. If a system of hypotheses has been derived from presuppositions dictated by a worldview, it usually cannot be reconciled with the available facts. Typical examples are geocentricity (refuted by Copernicus), and phlogiston chemistry (disproved by Lavoisier in 1774). It is hoped that this book will help to uproot the current evolutionary paradigm.
Speculation:
When a statement is based purely on discussion, fantasy, imagination, or contemplation and does not correspond to reality, it is speculation, or merely an intellectual game. Because no actual experimentation is involved, it is easy to make undiscoverable mistakes. In thought experiments, difficulties can easily be evaded, undesirable aspects can be suppressed, and contradictions can be deftly concealed. Thought experiments can probably raise questions, but cannot answer any; only actual experimentation can provide answers. In this sense, the “hypercycle” proposed by Manfred Eigen is pure speculation [G10, p. 153–155]. Mere speculation without experimentation and observation is not science, neither is pure deduction from arbitrary presuppositions, nor is a biased selection of observations. Even the most abstract theory should not lose contact with reality and experimentation; it must be empirically verifiable.1 Thought experiments as well as deductions from philosophical postulates not based on observation are speculations.
>Fiction (Latin fictio = fabrication, story):
A fiction is either a deliberate or an unintentional fantasy which is not based on reality. Sometimes a false assumption (fiction) can be introduced deliberately for the purpose of clarifying a scientific problem methodologically.
2.2 The Limits of Science and the Persistence of Paradigms
We have discussed different categories of laws of nature and can now realize that many statements are often formulated with far too much confidence and in terms which are far too absolute. Max Born (1882–1970), a Nobel laureate, clearly pointed this out with respect to the natural sciences [B4]:
Ideas like absolute correctness, absolute accuracy, final truth, etc. are illusions which have no place in any science. With one’s restricted knowledge of the present situation, one may express conjectures and expectations about the future in terms of probabilities. In terms of the underlying theory, any probabilistic statement is neither true nor false. This liberation of thought seems to me to be the greatest blessing accorded us by present-day science.
Another Nobel laureate, Max Planck (1858–1947), deplored the fact that theories which have long ago become unacceptable are doggedly adhered to in the sciences [P3, p 13]:
A new scientific truth is usually not propagated in such a way that opponents become convinced and discard their previous views. No, the adversaries eventually die off, and the upcoming generation is familiarized anew with the truth.
This unjustified adherence to discarded ideas was pointed out by Professor Wolfgang Wieland (a theoretical scientist, University of Freiburg, Germany) in regard to the large number of shaky hypotheses floating around [W4, p 631]:
Ideas originally formulated as working hypotheses for further investigation, possess an inherent persistence. The stability accorded established theories (in line with Kuhn’s conception), is of a similar nature. It only appears that such theories are tested empirically, but in actual fact observations are always explained in such a way that they are consistent with the pre-established theories. It may even happen that observations are twisted for this purpose.
The persistence of a paradigm which has survived the onslaught of reality for a long time, is even greater [W4, p 632]:
“When it comes to collisions between paradigms and empirical reality, the latter usually loses, according to Kuhn’s findings. He based his conclusions on the history of science and not on science theory. However, the power of the paradigm is not unlimited. . . . There are stages in the development of a science when empirical reality is not adapted to fit the paradigm; during such phases different paradigms compete. Kuhn calls these stages scientific revolutions. . . . According to Kuhn’s conception it is a fable that the reason why successful theories replace previous ones is because they perform better in explaining phenomena. The performance of a theory can be measured historically in quite different terms, namely the number of its sworn-in adherents.” Much relevant scientific data is lost because of the dictatorship of a false paradigm, since deviating results are regarded as “errors in measurement” and are therefore ignored.
A minimal requirement for testing whether a theory should be retained or whether a hypothesis should not yet be discarded or that a process could really work is that the relevant laws of nature should not be violated.
2.3 The Nature of Physical Laws
A fundamental metaphysical law is that of causality. This means that every event must have a cause, and that under the same circumstances a certain cause always has the same effects. For a better understanding of the laws of nature we will now discuss some basic aspects which are important for the evaluation and application of events and processes:
N1: The laws of nature are based on experience.
It is often asserted that the laws of nature are proven theorems, but we have to emphasize that the laws of nature cannot be proved! They are only identified and formulated through observation. It is often possible to formulate conclusions in exact mathematical terms, ensuring precision, brevity, and generality. Even though numerous mathematical theorems (except the initial axioms) can be proved,2 this is not the case for the laws of nature. A mathematical formulation of an observation should not be confused with a proof. We affirm: the laws of nature are nothing more than empirical statements. They cannot be proved, but they are nevertheless valid.
The fundamental law of the conservation of energy is a case in point. It has never been proved, because it is just as unprovable as all other laws of nature. So why is it universally valid? Answer: Because it has been shown to be true in millions of experiences with reality. It has survived all real tests. In the past, many people believed in perpetual motion, and they repeatedly invested much time and money trying to invent a machine that could run continuously without a supply of energy. Even though they were never successful, they rendered an important service to science. Through all their ideas and efforts, they demonstrated that the energy law cannot be circumvented. It has been established as a fundamental physical law with no known exceptions. The possibility that a counter example may be found one day cannot be excluded, even if we are now quite sure of its truth. If a mathematical proof of its truth existed, then each and every single non-recurrent possible deviation from this natural law could be excluded beforehand.
The unprovability of the laws of nature has been characterized as follows by R.E. Peierls, a British physicist [P1, p 536]:
Even the most beautiful derivation of a natural law . . . collapses immediately when it is refuted by subsequent research. . . . Scientists regard these laws as being what they are: Formulations derived from our experiences, tested, tempered, and confirmed through theoretical predictions and in new situations. Together with subsequent improvements, the formulations would only be accepted as long as they are suitable and useful for the systematization, explanation, and understanding of natural phenomena.
N2: The laws of nature are universally valid.
The theorem of the unity of nature is an important scientific law. This means that the validity of the laws of nature is not restricted to a certain limited space or time. Such a law is universally valid in the sense that it holds for an unlimited number of single cases. The infinitude of these single cases can never be exhausted by our observations. A claim of universal validity for an indefinite number of cases can immediately be rejected when one single counter example is found.3
In our three-dimensional world, the known laws of nature are universally valid, and this validity extends beyond the confines of the earth out through the entire physical universe, according to astronomical findings. When the first voyages to the moon were planned, it was logically assumed that the laws identified and formulated on earth were also valid on the moon. The laws of energy and of gravity were used to compute the quantities of fuel required, and when man landed on the moon, the assumption of universal validity was found to be justified. The law of the unity of nature (the universal validity of laws of nature) will hold until a counter example is found.
N3: The laws of nature are equally valid for living beings and for inanimate matter.
Any law which is valid according to N2 above, includes living beings. Richard P. Feynman (1918–1988), Nobel laureate for physics (1965), writes [F1, p 74]:
The law for conservations of energy is as true for life as for other phenomena. Incidentally, it is interesting that every law or principle that we know for “dead” things, and that we can test on the great phenomenon of life, works just as well there. There is no evidence yet that what goes on in living creatures is necessarily different, so far as the physical laws are concerned, from what goes on in non-living things, although the living things may be much more complicated.
All measurements (sensory organs), metabolic processes, and transfers of information in living organisms strictly obey the laws of nature. The brilliant concepts realized in living beings are based on refined and very ingenious implementations of the laws of nature. For example, the sensitivity of human hearing attains the physically possible limits by means of a combination of determining factors [G11, p 85–88]. The laws of aerodynamics are employed so masterfully in the flight of birds and insects that similar performance levels have not yet been achieved in any technological system (see Appendix A3.4.4).
N4: The laws of nature are not restricted to any one field of study.
This theorem is actually redundant in the light of N2 and N3, but it is formulated separately to avoid any possibility of misunderstanding.
The energy conservation law was discovered by the German doctor and physicist Julius Robert Mayer (1814–1878) during an extended voyage in the tropics. He was a medical officer and he formulated this law when contemplating the course of organic life. Although it was discovered by a medical officer, nobody considered the possibility of restricting the validity of this theorem to medical science only. There is no area of physics where this theorem has not been decisive in the clarification of relationships. It is fundamental in all technical and biological processes.
The second law of thermodynamics was discovered by Rudolf Clausius in 1850 during the course of technological research. He formulated it for thermodynamic processes, but this theorem is also valid far beyond all areas of technology. Even the multiplicity of interactions and conversions in biological systems proceed according to the requirements of this law of nature.
Later in this book we will formulate several theorems on information, but the reader should not labor under the impression that their validity is restricted to the areas of informatics or technology. On the contrary, they have the same impact as laws of nature and are therefore universally applicable in all cases where information is involved.
N5: The laws of nature are immutable.
All known observations indicate that the laws of nature have never changed. It is generally assumed that the known laws are constant over time, but this is also merely an observation that cannot be proven.
Comment: Of course, He who has invented and established the laws of nature is also able to circumvent them. He is Lord of the laws of nature, and in both the Old and the New Testaments, we find numerous examples of such events (see theorem N10b).
N6: The laws of nature are simple.
It should be noted that the laws of nature can mostly be formulated in very simple terms. Their effects are, however, often complex, as may be seen in the following example. The law of gravity has been described as the most important generalization which human intellect has been fortunate enough to discover. It states that two bodies exert a force on each other which is inversely proportional to the square of their distance and directly proportional to the product of their masses. It can be formulated mathematically as follows:
F = G x m1 x m2 / r2
The force F is given by a constant (the so-called gravitational constant, G) multiplied by the product of the two masses m1 and m2, divided by the square of the distance r. In addition, it can be mentioned that the effect of a force on an object is to accelerate it. This means that the velocity of an object acted on by a force changes faster when its mass is smaller. Now almost everything worth knowing about the law of gravity has been said. When this law is used to compute the orbits of the planets, it immediately becomes clear that the effects of a simple natural law can be very complex. When the relative motions of three bodies are analyzed in terms of this law, the mathematical formulations become quite intractable.
Faraday’s law of electrolysis states that the quantity of matter separated out during electrolysis is proportional to the electrical current and to its duration (e.g., electroplating with copper or gold). This formulation may seem to be very mathematical, but what it really means is that one unit of charge is required to separate one atom from the molecule it belongs to.
Conclusion: Laws of nature may be expressed and formulated verbally to any required degree of precision. In many cases, it is possible and convenient to formulate them mathematically as well. As Feynman states [F1, p 41]: “In the last instance mathematics is nothing more than a logical course of events which is expressed in formulas.” Sir James H. Jeans (1877–1946), the well-known British mathematician, physicist, and astronomer, said [F1, p 58]: “The Great Architect seems to be a mathematician.”
N7: The laws of nature are (in principle) falsifiable.
To be really meaningful, a theorem must be formulated in such a way that it could be refuted if it was false. The fact that the laws of nature can be formulated the way they are cannot be ascribed to human ingenuity, but is a result of their being established by the Creator. After a law has been formulated, we discover that it could in principle very easily be negated if invalid. This is what makes these laws so important and accords them their great range of applicability.
There is a German saying which goes like this: “When the cock crows on the dungheap, the weather will change, or it will remain as it is.” This statement cannot be falsified; therefore, it is worthless. In contrast, the energy conservation law is very susceptible to falsification: “Energy cannot be created, neither can it be destroyed.” The formulation is strikingly simple, and it seems to be very easy to refute. If it was not valid, one could devise an experiment where the before and after energy equilibria did not balance. Nevertheless, it has not yet been possible to come up with one single counterexample. In this way, a theorem which is based on observation is accepted as a law of nature.
N8: The laws of nature can be expressed in various ways.
Different ways of expression can be employed for any given natural law, depending on the mode of application. If the question is whether an expected result could be obtained or not, it would be advantageous to describe it in the form of an impossibility theorem, and when calculations are involved, a mathematical formulation is preferable. The energy law could be formulated in one of four different ways, depending on the circumstances:
- a) Energy cannot be created from nothing; neither can it be destroyed.
- b) It is impossible to construct a machine which can work perpetually once it has been set in motion, without a continuous supply of energy (b follows directly from a).
- c) E = constant (The energy of a system is constant.)
- d) dE/dt = 0 (The balance of the total of all energies E of a system does not change, meaning that the derivative of energy versus time is zero.)
N9: The laws of nature describe reproducible results.
When a natural law has been identified as such, its validity could be established anew in each and every case where it is applicable. Reproducibility is an essential characteristic of the laws of nature. One could drop a stone as often as you like from various heights, and the law of gravity would always be obeyed. It is thus possible to make predictions about the behavior and interrelationships of things by means of the laws of nature. The laws of nature are eventually established through continual verification.
The nine above-mentioned general but fundamental theorems about the nature of the laws of nature, N1 to N9, have all been derived from experience. Their correctness cannot be proved, but can be tested repeatedly in the real world. We now formulate a tenth theorem which depends, however, on the personal view of the user. For this reason we present two different versions, theorems N10a and N10b. In the one case, the existence of God is denied, and in the second case, He is accepted as the Prime Cause. Both views are equally a question of belief and conviction. In the case of any given model, we have to decide which one of the two assumptions would be more useful.
N10a: Natural events can be explained without God.
This assumption can be used in all cases where the laws of nature are applied to existing or planned systems. An analysis of the energy equilibrium when ice melts is an example of an existing system, while an example of a planned system is the building of a new space vehicle. In actual fact, most effects of the laws of nature can be explained and computed without reference to God (e.g., free fall). All attempts to explain the origin of life by means of models where God as initiator is ignored are based on theorem N10a.
It is necessary to formulate an important alternative theorem for those who acknowledge the God of the Bible, namely, when did the laws of nature begin to operate, and what is God’s position in regard to these laws? These questions cannot be solved through observation, and we require some knowledge of the Bible as background.
N10b: The present laws of nature became operational when creation was completed.
The laws of nature are a fundamental component of the world as we know it, and they indicate that the Creator sustains all things (Col. 1:17, Heb. 1:3). These laws were installed during the six creation days and thus cannot be regarded as prerequisites for creation, since they themselves were also created. It is very emphatically denied that God’s creative acts could be explained in terms of the present laws of nature. At the end of the six days of creation, everything was complete—the earth, the universe, the plants, animals, and man:
"By the seventh day God had finished the work he had been doing” (Gen. 2:2).
If one tried to explain the actual creative acts in terms of the laws of nature, one would very soon be trapped in an inextricable net of speculations. This holds both for creationists and for supporters of evolution. The latter endeavor to explain the origin of life by means of laws of nature, but nobody has yet been able to do this! We therefore conclude: All the laws of nature have only been in operation since the completion of creation.
If God is the Creator of the laws of nature, then He himself is not subject to them. He can use them freely and can, through His omnipotence, limit their effects or even nullify them. The miracles described in the Bible are extraordinary events where the effects of particular laws of nature were completely or partially suspended for a certain period or in a certain place. When Jesus walked on the water (Matt. 14:22–33), He, as the Son of God and Lord of everything, nullified the law of gravity. We read in Matthew 24:29 that “the heavenly bodies will be shaken” (this could also be translated as “the forces of the heavens will be shaken”) when Jesus comes again. In the language of physics, this means that the present finely tuned equilibria of the various kinds of forces in the universe will be changed by the Creator, with the result that the orbits of the earth and the moon will become entangled and the stars will seem to move erratically:
“The earth reels like a drunkard, it sways like a hut in the wind”(Isa. 24:20).
The moment that historical questions (e.g., about the origin of the world and of life) or future events (like the end of the earth) are considered, then N10a is entirely useless.
2.4 The Relevance of the Laws of Nature
R1: The laws of nature provide us with a better understanding of natural phenomena and events.
Without the laws of nature we would have had a very limited knowledge of the physical, chemical, astronomical, and biological processes occurring in the world around us. The progress of science mostly relies on the fact that fundamental principles are identified and classified, even when different effects are studied.
R2: The laws of nature enable us to make predictions.
Because of N5 and N9, the expected course of observed processes can be predicted. Exactly because of this certainty, it is in many cases possible to compute beforehand what will happen. If, for example, a stone is dropped, one can calculate what its speed will be after two seconds.
R3: The laws of nature make technological development possible.
All engineering constructions and all technical manufacturing processes are based on the laws of nature. The reason why the construction of a bridge, a car, or an aircraft can be planned in advance, is that the relevant laws of nature are known. Without knowledge of the laws of nature, there could have been neither chemical nor pharmaceutical industries.
R4: By means of the laws of nature, it is possible to determine beforehand whether an envisaged process would be realizable or not.
This is a very important application of the laws of nature. Some time ago I received a comprehensive piece of work consisting of many diagrams, calculations, and explanations from an inventor with the request that the proposed construction should be checked. This person envisioned an extremely complex system of pumps and pipes which would be able to drive a hydraulic motor. It was, however, immediately clear, without my having to do any calculations or tests, that such an arrangement could never work because it violated the energy law. In many cases, the laws of nature enable one to make conclusions beforehand without having to study the details.
R5: The laws of nature are applicable to cases formerly unknown.
The fact that the laws of nature can be transferred to new cases is of special importance. Up to the present time, nobody has been able to imitate the process of photosynthesis which takes place in every blade of grass. If and when such an endeavor may eventually be planned, then all proposed methods which violate any one of the laws could be rejected in advance. Any such design could be eliminated as useless in the conceptual phase. In addition, past results which were accepted in the light of some paradigm could also be evaluated. Is it, for example, possible that information could have originated in a postulated primeval soup? This question is discussed further in chapter 6.
R6: One can employ a known natural law to discover another one.
It has happened time and again in the history of science that a new law has been discovered using the validity of a known law. If the law of gravity had not been known, then the behavior of the moons of Jupiter could not have been investigated properly. Observations of their motions made it possible to compute the speed of light, which is an important physical constant.
The orbits of the planets cannot be exactly elliptical (as would be required if the gravitational pull of the sun was the only force acting on them), as required by Newton’s law, since they are not only under the gravitational influence of the sun, but they also affect one another gravitationally to a lesser extent. John Couch Adams (1819–1892), a British astronomer and mathematician, computed the expected perturbations caused by their mutual gravitational attractions of the orbits of the then known major planets, Jupiter, Saturn, and Uranus. The French astronomer Urban J.J. Leverrier (1811–1877) also computed the deviations of these orbits from the perfect Kepler ellipses independently. It was found that Jupiter and Saturn “lived up to the expectations,” but Uranus exhibited deviant behavior.
Relying on the validity of Newton’s law, both astronomers were able to deduce the position of a hitherto unknown planet from these irregularities. Each of them then approached an observatory with the request to look for an unknown planet in such and such a celestial position. This request was not taken seriously at one observatory; they regarded it as absurd that a pencil-pusher could tell them where to look for a new planet. The other observatory responded promptly, and they discovered Neptune. Leverrier wrote to the German astronomer Johann Gottfried Galle (1812–1910), who then discovered Neptune very close to the predicted position.
2.5 The Classification of the Laws of Nature
When one considers the laws of nature according to the ways they are expressed, one discovers striking general principles which they seem to obey. The laws can accordingly be classified as follows.
Conservation theorems:
The following description applies to this group of laws: a certain number, given in a suitable unit of measurement, can be computed at a specific moment. If this number is recomputed later after many changes may have occurred in nature, its value is unchanged. The best-known law in this category is the law of the conservation of energy. This is the most abstract and the most difficult of all the conservation laws, but at the same time it is the most useful one, since it is used most frequently. It is more difficult to understand than the laws about the conservation of mass (see footnote 5), of momentum, of rotational moment, or of electrical charge. One reason is that energy can exist in many different forms like kinetic energy, potential energy, heat energy, electrical energy, chemical energy, and nuclear energy. In any given process, the involved energy can be divided among these forms in many different ways, and a number can then be computed for each kind of energy. The conservation law now states that the sum of all these numbers stays constant irrespective of all the conversions that took place during the time interval concerned. This sum is always the same at any given moment. It is very surprising that such a simple formulation holds for every physical or biological system, no matter how complex it may be.
Equivalence theorems:
Mass and energy can be seen to be equivalent in terms of Einstein’s famous formula E = m x c2. In the case of atomic processes of energy conversion (nuclear energy) there is a small loss of mass (called the deficit) which releases an equivalent amount of energy, according to Einstein’s formula.
Directional theorems:
From experience in this world we know that numerous events proceed in one sense only. A dropped cup will break. The converse event, namely that the cup will put itself together and jump back into our hand, never happens, however long we may wait. When a stone is thrown into a pool of water, concentric waves move outward on the surface of the water. This process can be described mathematically, and the resulting equations are equally valid for outward moving waves and for the imaginary case if small waves should start from the edge and move concentrically inward, becoming larger as they do so. This converse process has never been observed, although the first event can be repeated as often as we like.
For some laws of nature, the direction does not play any role (e.g., energy), but for others the process is unidirectional, like a one-way street. In the latter case, one can clearly distinguish between past and future. In all cases where friction is involved, the processes are irreversible; they proceed in one direction only. Examples of such laws are the law of entropy (see the appendix), the chemical principle of Le Chatelier (Henry-Louis Le Chatelier, French chemist, 1850–1936; see Q20 p. 128–130), and the law of mass action.
Impossibility theorems:
Most laws of nature can be expressed in the form: “It is impossible that. . . .” The energy law for example, can be stated as follows: “It is impossible that energy can come into existence by itself.” R. Clausius formulated the second law of thermodynamics as an impossibility: “Heat cannot of itself pass from a colder to a hotter body” The impossibility theorems are very useful because they effectively distinguish between possible and impossible events. This type of scientific formulation will be encountered frequently when we come to the information theorems.

Figure 6: Geometrically impossible bodies
Geometrical impossibilities can also be devised. Three different geometric representations appear in Figure 6, but such bodies are just as impossible to construct as it is to expect results that are precluded by laws of nature.
Laws which describe processes:
If the future (prognosis) or the past (retrognosis) states of a system can be described when the values of the relevant variables are known for at least one moment in time, such a formulation is known as a process law. A typical physical example is the description of radioactive decay.
Co-existence laws:
These describe the simultaneous existence of the properties of a system. The formula describing the state changes of an ideal gas, p x v = R x T, is a typical physical coexistence law. The values of the three quantities, pressure p, specific volume v, and absolute temperature T, comprise a complete description of the “state” of an ideal gas. This means that it does not depend on the previous history of the gas, and neither does it depend on the way the present pressure or the present volume has been obtained. Quantities of this type are known as state variables.
Limit theorems:
Limit theorems describe boundaries that cannot be overstepped. In 1927, the German physicist Werner Heisenberg (1901–1976) published such a theorem, namely the so-called uncertainty principle of Heisenberg. According to this principle, it is impossible to determine both the position and the velocity of a particle exactly at a prescribed moment. The product of the two uncertainties is always greater than a specific natural constant, which would have been impossible if the uncertainties were vanishingly small. It follows, for example, that certain measurements can never be absolutely exact. This finding resulted in the collapse of the structure of the then-current 19th century deterministic philosophy. The affirmations of the laws of nature are so powerful that viewpoints which were held up to the time they are formulated, may be rapidly discarded.
Information theorems:
In conclusion, we mention that there is a series of theorems which should also be regarded as laws of nature, although they are not of a physical or a chemical nature. These laws will be discussed fully in this book, and all the previously mentioned criteria, N1 to N9, as well as the relevance statements R1 to R6, are also valid in their case.
2.6 Possible and Impossible Events
The totality of all imaginable events and processes can be divided into two groups as in Figure 7, namely,
- possible events
- impossible events.
Possible events occur under the “supervision” of the laws of nature, but it is in general not possible to describe all of them completely. On the other hand, impossible events could be identified by means of the so-called impossibility theorems.
Impossible events can be divided into two groups: those which are “fundamentally impossible” and those which are “statistically impossible.” Events which contradict, for example, the energy law are impossible in principle because this theorem even holds for individual atoms. On the other hand, radioactive decay is a statistical law which is subject to the probability theorems and cannot be applied to individual atoms, but in all practical cases, the number of atoms is so immense that an “exact” formulation can be used, namely n(t) = n0 x e -k x t. The decay constant k does not depend on temperature, nor on pressure, nor on any possible chemical bond. The half-life T is given by the formula T = ln 2/k; this indicates the time required for any given quantity n0 to diminish to half as much, n0/2. Since we are dealing with statistical events, one might expect that less than half the number of atoms or appreciably more then half could have decayed at time T. However, the probability of deviation from this law is so close to zero that we could regard it as statistically impossible. It should be clear that impossible events are neither observable nor recognizable nor measurable. Possible events have in general either been observed, or they are observable. However, there are other possible events about which it can be said that they
—cannot or cannot yet be observed (e.g., processes taking place in the sun’s interior)
—are in principle observable, but have never been observed
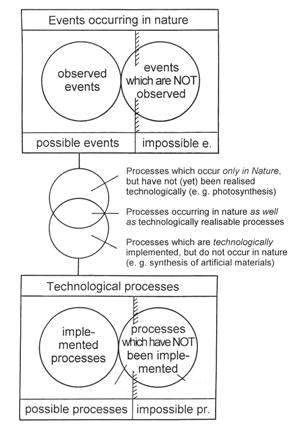
Figure 7: Possible and impossible events in nature and in technological processes.
Thus far, we have only discussed natural events, but now we can apply these concepts to technological processes (in the widest sense of the word, comprising everything that can be made by human beings). The following categories are now apparent:
- possible processes
- impossible processes: proposed processes of this kind are fundamentally unrealizable, because they are precluded by laws of nature.
1.1 already implemented
1.2 not yet implemented, but realizable in principle
The distinctions illustrated in Figure 7 follow from a comparison of possible events in nature and in technology, namely:
- processes which occur only in nature, but have not (yet) been realized technologically (e.g., photosynthesis, the storage of information on DNA molecules, and life functions);
- processes occurring in nature which are also technologically realizable (e.g., industrial synthesis of organic substances);
- processes which have been technologically implemented, but do not occur in nature (e.g., synthesis of artificial materials).
In the Beginning Was Information
Between the covers of this book may well be the most devastating scientific argument against the idea that life could form by natural processes.
Read OnlineFootnotes
- Verification (Latin verus = true, facere = make): Verification means that a statement is tested experimentally. The result of such a verification is not generally valid, however. It holds strictly only for cases which have actually been confirmed because the possibility that hitherto unknown counterexamples may exist cannot be excluded. If one contradictory case is found, then the statement is rejected (falsified!). This can also be expressed as follows: It is not possible to verify a theory; a theory can only be falsified. A theory is good if it could be falsified very easily, and when it survives all open criticisms and tests, it can be accepted.
- Provability: The German mathematician David Hilbert (1862–1943) held the optimistic view that every mathematical problem could be resolved in the sense that a solution could be found, or that it could be proved that a solution was impossible, for example the quadrature (squaring) of a circle. He, therefore, said in his famous talk in Königsberg (1930) that there were no unsolvable problems: “We must know, we will know.” Kurt Gödel (1906–1978), the well-known Austrian mathematician, rejected this view. He showed that, even in a formal system, not all true theorems could be proved. This statement, called the first incompleteness theorem of Gödel, was quite a revolutionary result. Because of the far-reaching effects for mathematics and for science theory, Heinrich Scholz called Gödel’s work “A critique of pure reason from the year 1931.”
- Amendments to formulated laws of nature: An established natural law loses its
universal validity when one single counterexample is found. However, it is often
only necessary to change the formulation to describe the actual law more precisely.
We should, therefore, distinguish between the actual law as it operates in nature,
and its formulation in human terms. More precise formulations do not invalidate
an “approximately formulated law,” but do provide a better description of reality.
In the following two cases, the original formulations were too narrow, and had to
be revised:
Example 1: The classical laws of mechanics lost their validity when appreciable fractions of the speed of light were involved. They were extended by the more precise special theory of relativity because the relativistic effects could not be observed when velocities were small. The laws of classical mechanics are a good enough approximation for general purposes (e.g., construction of machines), but, strictly speaking, their original formulations were incorrect.
Example 2: The law of conservation of mass had to be reformulated to become a general law of the conservation of mass and energy when nuclear reactions were involved (loss of mass, E = m x c2). Nevertheless, the law of mass conservation is a potent law of nature.
Recommended Resources

Answers in Genesis is an apologetics ministry, dedicated to helping Christians defend their faith and proclaim the good news of Jesus Christ.
- Customer Service 800.778.3390
- Available Monday–Friday | 9 AM–5 PM ET
- © 2026 Answers in Genesis


