
Protein Mutational Context Dependence: A Challenge to Neo-Darwinism Theory: Part 1
Originally published in Journal of Creation 17, no 1 (April 2003): 117-127.
Whenever amino acids can be changed at a residue position, it is generally assumed this mutation is compatible with all other tolerated residue substitutions. We show here empirically that this cannot be assumed. The implications for evolutionary theory are two-fold. First, finding an initial viable sequence by chance, upon which natural selection could act, becomes overwhelmingly improbable. Second, improvement of the protein functionality by random mutations faces unsurmountable statistical odds.
According to neo-Darwinism, genes to produce novel protein families arose by random mutations in DNA plus natural selection. In the absence of similar genes to provide a starting point, thousands of novel genes must have arisen de novo long ago. The origin of genes with very little sequence variability, such as those coding for ubiquitin or histone H-4,1–5 must somehow be accounted for in spite of the vastly greater proportion of non-functional alternatives.
Selective advantage would favour the descendents of a fortunate mutant.
Selective advantage would favour the descendents of a fortunate mutant. If these survive many generations, they would eventually out-populate the non-mutant competitors. Further evolutionary improvements on a gene would then be restricted to a narrower range of sequences.
Variants of a given protein are often found in all single and multicellular organisms. Therefore, common ancestors presumably generated many new genes long before the Cambrian Explosion (ca. 550 million years ago according to current evolutionist thinking).
Usually different amino acids are tolerated at many residue positions of proteins. Some mistakenly assume this implies that all acceptable single residue mutations are viable in the presence of all other acceptable single residue alternatives. I drew attention to this matter in this Journal.6–7 If wrong, it means that the number of functional possibilities for both an original gene starting point and the theoretical intermediate evolutionary paths are far more restricted than assumed.
I wish to demonstrate two points in this paper.
(a) Finding an evolutionary starting point for novel genes is highly improbable.
In an earlier paper8 Heisig and I examined the variability of cytochrome c. It was selected because of the large number of sequence data available and the information theory calculations published by Yockey. Although only a third as large as an average protein, the available data suggested a proportion of about 1 out of 1065 of random sequences would be functional. Even if all organisms were dedicated to evolutionary trial and error attempts for a billion years preceding the Cambrian Explosion, a single minimally functional cytochrome c gene sequence is unlikely to be obtained.
It could be argued that the known data involves optimized cytochrome c and that the proportion of candidate starting points may be greater.9 Contra this argument, I will show there is evidence that the implied assumption of amino acid contextual independence grossly overestimates the actual number of suitable starting candidates.
(b) Evolutionary computer models use false premises.
Evolutionary computer models assume there is a continuum in protein sequence space which links minimally functional to highly optimised variants. Many paths are presumed to be available for evolutionary attempts which can lead to ever narrower sets of variants. This trend, if true, would represent an increase in information content in the Shannon sense.
The probability that a random DNA sequence could produce a novel, highly optimized gene (including the coding and regulatory sequences), is vanishingly small. It is also clear that minimally functional proteins would provide negligible selective advantage and such genes would have little chance of fixing in the population. Therefore, neo-Darwinian theory requires the following assumption: on average, the variety of viable primitive sequences must increase steadily as one goes back in time. Only in this manner might one lineage or the other survive and be fine-tuned by random mutations.
Visualize a box which represents the collection of all alternative amino acids for a short stretch of a protein. The members need not be contiguous on the extended polymer structure. Evolutionary theory requires that on average these boxes become smaller, i.e. contain fewer members, as we climb the fitness pyramid. The different proteins built by using members from a given box possess about the same biological effectiveness, meaning survival chances for the organism, ceteris paribus. Boxes separated by one vertical level generally differ by one amino acid, since mutations which change multiple amino acids within a narrow part of a protein in one generation are negligibly rare. Presumably many alternative evolutionary pathways would be available to progress upwards towards a better protein, since smaller ‘boxes’ could be reached in different orders within the same horizontal strata.
We cannot realistically test the functionality of all (n)20 alternatives of an n-residue protein. But we can evaluate ‘evolutionary wedges’, consisting of stretches a few residues long, of the total protein. The vertical layers of boxes must contain only functional intermediates and be linked by feasible random mutations.
Two data sets have been found in the literature, which permit these evolutionary assumptions to be examined. A more detailed paper will be presented in part two. We shall explore here how these kinds of experiments can be designed and evaluated.
Experimental overview
Lim and Saur17 studied a seven-residue portion of the inner core of phage λ-repressor protein (Appendix 1). Instead of randomising all seven positions at the same time, three experiments were performed in which sets of three and four residues were randomly varied.10 In Experiment 1, combinations of three residues were examined: Val-36, Met-40 and Val-47. In Experiment 2, four residues were randomised: Leu-18, Val-36, Val-47 and Phe-51. In Experiment 3, three residues: Leu-18, Leu-57 and Leu-65. The three-letter codes refer to amino acids (Table 1) and the number to position along the protein.
Functional and partially functional mutants were identified from among the tens of thousands of random mutations generated, of which statistically significant numbers were sequenced. The method is able to generate all possible amino acid alternatives across the regions studied but uses only 32 of the genetic 64 codons (3 base-pairs) possible (Table 1).
Buried here is valuable data for our purposes. The authors did not identify which of the three experiments led to the sequences11 shown in Table 2, but we can make the necessary deductions.
Table 1. All possible codons which could be generated by the experimental protocol10,17 (AA = Amino Acid).
| U | C | A | G | 3rd | |
|---|---|---|---|---|---|
| U | Phe | Ser | Tyr | Cys | C |
| Leu | Ser | Stop | Trp | G | |
| C | Leu | Pro | His | Arg | C |
| Leu | Pro | Gln | Arg | G | |
| A | Ile | Thr | Asn | Ser | C |
| Met | Thr | Lys | Arg | G | |
| C | Val | Ala | Asp | Gly | C |
| Val | Ala | Glu | Gly | G |
| 1-letter code |
3-letter code |
No. of codons coding for the AA |
|---|---|---|
| AA | Repeats | |
| A | Ala | 2 |
| R | Arg | 3 |
| N | Asn | 1 |
| D | Asp | 1 |
| C | Cys | 1 |
| Q | Gln | 1 |
| E | Glu | 1 |
| G | Gly | 2 |
| H | His | 1 |
| I | Ile | 1 |
| L | Leu | 3 |
| K | Lys | 1 |
| M | Met | 1 |
| F | Phe | 1 |
| P | Pro | 2 |
| S | Ser | 3 |
| T | Thr | 2 |
| W | Trp | 1 |
| Y | Tyr | 1 |
| V | Val | 2 |
Results
The results from Experiment 3 are easiest to analyse.12 Table 3 provides an overview of their results and Table 2 shows protein variants which were at least partially functional. The number of functional and partially functional variants identified from a random set of 15,000 members are shown in Table 4: 18 mutants differ by one residue from the modern sequence; 4 by two residues and only 1 by three residues. This is the opposite trend expected by evolutionary theory: the ‘boxes’ further back in time, which differ most from the modern version, should contain far more variants than today’s finely tuned ones. The assumption of contextual independence alone implies that 5 x 6 x 7 = 210 functional variants would exist which differ by three residues from the wild type, whereas only one was found.13 From an evolutionary point of view, this observation presents the worse of all scenarios: fewer acceptable candidates as a starting point and poorer functionality at the same time! This observation discredits the assumption, that it is statistically more plausible to obtain highly-tuned genes via step-by-step improvements than through a single ‘freak’ accident.
Table 2. Functional alternatives within a 7-residue portion of lambda-repressor protein. Number of amino acid (AA) differences from the wild type sequence. Mutants are shown in darker shade.
| Fully functional mutants | ||||||||
|---|---|---|---|---|---|---|---|---|
| Wild | Leu | Val | Met | Val | Phe | Leu | Leu | |
| 18 | 36 | 40 | 47 | 51 | 57 | 56 | ||
| L | V | M | V | F | L | L | ||
| 1-AA | L | I | M | V | F | L | L | |
| L | V | L | V | F | L | L | ||
| L | V | M | I | F | L | L | ||
| L | V | M | V | L | L | L | ||
| L | V | M | V | M | I | L | ||
| L | V | M | V | F | M | L | ||
| L | V | M | V | F | L | F | ||
| L | V | M | V | F | L | M | ||
| L | V | M | V | F | L | V | ||
| 2-AA | L | I | M | V | L | L | L | |
| L | M | M | V | I | L | L | ||
| L | V | L | I | F | L | L | ||
| L | L | M | I | F | L | L | ||
| L | V | M | L | L | L | L | ||
| L | V | M | T | L | L | L | ||
| 3-AA | A | L | M | V | L | L | L | |
| I | L | M | V | L | L | L | ||
| L | A | M | L | L | L | L | ||
| L | I | C | I | F | L | L | ||
| L | I | L | I | F | L | L | ||
| L | L | M | I | L | L | L | ||
| L | L | M | L | L | L | L | ||
| L | M | M | I | M | L | L | ||
| L | T | M | L | L | L | L | ||
| V | V | M | I | L | L | L | ||
| V | V | M | L | L | L | L | ||
| 4-AA | I | L | M | L | L | L | L | |
| V | T | M | I | L | L | L | ||
| V | M | M | I | L | L | L | ||
| Partially functional | ||||||||
| 1-AA | A | V | M | V | F | L | L | |
| C | V | M | V | F | L | L | ||
| M | V | M | V | F | L | L | ||
| V | V | M | V | F | L | L | ||
| I | V | M | V | F | L | L | ||
| L | A | M | V | F | L | L | ||
| L | C | M | V | F | L | L | ||
| L | L | M | V | F | L | L | ||
| L | T | M | V | F | L | L | ||
| L | V | V | V | F | L | L | ||
| L | V | A | V | F | L | L | ||
| L | V | M | T | F | L | L | ||
| L | V | M | V | I | L | L | ||
| L | V | M | V | V | L | L | ||
| L | V | M | V | C | L | L | ||
| L | V | M | V | F | P | L | ||
| L | V | M | V | F | V | L | ||
| L | V | M | V | F | C | L | ||
| L | V | M | V | F | F | L | ||
| L | V | M | V | F | L | A | ||
| L | V | M | V | F | L | C | ||
| L | V | M | V | F | L | S | ||
| L | V | M | V | F | L | T | ||
| Partially functional | ||||||||
|---|---|---|---|---|---|---|---|---|
| Leu | Val | Met | Val | Phe | Leu | Leu | ||
| 18 | 36 | 40 | 47 | 51 | 57 | 65 | ||
| L | V | M | V | F | L | L | ||
| 2-AA | A | V | M | V | F | M | L | |
| L | A | M | I | F | L | L | ||
| L | A | M | L | F | L | L | ||
| L | C | L | V | F | L | L | ||
| L | I | M | T | F | L | L | ||
| L | I | V | V | F | L | L | ||
| L | L | I | V | F | L | L | ||
| L | L | L | V | F | L | L | ||
| L | L | V | V | F | L | L | ||
| L | M | M | I | F | L | L | ||
| L | M | M | L | F | L | L | ||
| L | T | L | V | F | L | L | ||
| L | T | M | I | F | L | L | ||
| L | V | A | I | F | L | L | ||
| L | V | C | I | F | L | L | ||
| L | V | C | M | F | L | L | ||
| L | V | I | C | F | L | L | ||
| L | V | I | I | F | L | L | ||
| L | V | L | A | F | L | L | ||
| L | V | L | T | F | L | L | ||
| L | V | V | I | F | L | L | ||
| V | V | M | V | F | F | L | ||
| V | V | M | V | F | I | L | ||
| V | V | M | V | F | L | F | ||
| 3-AA | A | V | M | V | F | M | I | |
| L | A | M | F | L | L | L | ||
| L | C | L | I | F | L | L | ||
| L | C | M | M | L | L | L | ||
| L | C | M | F | V | L | L | ||
| L | I | A | I | F | L | L | ||
| L | I | V | L | F | L | L | ||
| L | L | L | I | F | L | L | ||
| L | L | L | L | F | L | L | ||
| L | L | M | I | V | L | L | ||
| L | L | M | L | V | L | L | ||
| L | L | V | I | F | L | L | ||
| L | M | L | I | F | L | L | ||
| L | M | M | T | L | L | L | ||
| M | L | M | V | L | L | L | ||
| M | V | M | I | L | L | L | ||
| V | V | M | L | I | L | L | ||
| 4-AA | C | L | M | I | L | L | L | |
| M | I | M | I | L | L | L | ||
| V | C | M | L | L | L | L | ||
| V | L | M | L | L | L | L | ||
Table 3. Overview of results reported.17
| Experiment no. | 1 | 2 | 3 |
| No. of amino acids varied | 3 | 4 | 5 |
| No. of alternative sequences possible | 80,000 | 160,000 | 8,000 |
| No. of mutants generated | 20,000 | 40,000 | 15,000 |
| No. of mutants which survived | 266 | 92 | 36 |
| Mutants sequenced | 102 | 30 | 35 |
| Extrapolated active + fully functional sequences | 1.7% | 0.6% | 0.4% |
We consider the following question: of all 203 = 8,000 sets of three amino acid candidates possible, how many were actually produced in Experiment 3 by the 15,000 random samples generated? 36 survivors were found comprising 23 unique amino acid sequences (Tables 2 and 4). This confirms that many duplicate protein mutants were produced by the 15,000 trials, since synonymous codons get generated (alternative sets of 3 DNA base pairs can code for the same amino acid). Amongst the 15,000 sets of three codons are also UAG or Stop codons, which produce non-viable, truncated proteins.
I derived a recursive formula (Appendix 2) to estimate statistically the number of different codons generated by the 15,000 members:
yj = yj-1 + n/(n-j+1) (1)
where yj is the average number of trials (mutants) needed to generate j different codons; n are the (32)3 possible14 different sets of three codons; y1=1, and the iteration must be repeated as long as the number of trials yj does not exceed the number of available mutants (yj≤15,000 in Experiment 3). The value of interest is the resulting j. Java (Appendix 3) and Excel computer programs,15 provided to TJ editorial staff, show that on average 12,036 unique codons would be generated by the protocol for Experiment 3.
Possibility of experimental bias
Table 4. All acceptable alternatives found (abstracted from Table 3).
| 1-AA Mutants | ||
|---|---|---|
| Leu-18 | Leu-57 | Leu-35 |
| A | I | F |
| C | M | M |
| M | P | V |
| V | V | A |
| I | C | C |
| F | S | |
| T | ||
| 2-AA Mutants | ||
| Leu-18 & Leu-57 | Leu-13 & Leu-65 | Leu-57 & Leu-65 |
| AM | VF | |
| VF | ||
| VI | ||
| 3-AA Mutants | ||
| Leu-18 & Leu-57 & Leu-65 |
||
| AMI | ||
We must exclude the possibility that the experimental design would produce more mutants which differ by only one amino acid from the wild type, than variants which differ by multiple amino acids.
Let us examine what the coding pattern and random base pairs actually generate. Of twenty possible residues, three can be coded by three different codons (Arg, Leu and Ser; see Table 1) according to the experimental design, whereas five residues are coded by two different codons and twelve residues by only a single codon. We see in Table 5 that all possible codons can be organized into 10 coding patterns (which exclude a Stop codon), depending on how many synonymous codons are used.
Perhaps the experiment generated statistically too few mutants which differ by three codons from today’s sequence. Conceivably many of these could be represented by amino acids which are generated by only one codon, such as pattern {1;1;1} in Table 5. We shall now see that this is not the case.
Each of the 12,036 unique codons belong to one of five categories: those generating amino acids which differ between 0 and 3 from the wild type; and those which include at least one Stop codon. The decrease in number of viable mutants with distance from the wild type (Table 4) is opposite to what we expect on the basis of neo-Darwinian theory and from statistical considerations. In Table 6, column 4 we see that statistically about 100 times more mutants would be generated which differ by three amino acids than by one amino acid from the wild type. This is due to two factors:
the proportion of unique amino acid sequences generated per unique codon sequence increases (column 4), and
the variety of possible unique codons themselves increases (column 2).
If enough mutants were prepared to test all possible amino acid alternatives in the three positions, we would expect about 2.7 times more of each kind of mutant (i.e. differing by one, two or three residues), as summarized in column 7 of Table 6.
The relative proportion of mutants differing by one to three residues from the wild type remains unchanged from the experimental results shown in Table 4. About 36.7% of all codon variants possible were generated in Experiment 3, and this is statistically representative of all possible codons.
We conclude then, that only two or three viable mutants out of 6,859 possibilities, which differ by three amino acids from the wild type, would be found (with at best minimal functionality, under laboratory conditions).
Equation (1) shows that on average one would need 326,843 random mutants to generate all 32,768 codon alternatives. Figure 1 illustrates what was actually done: 15,000 mutants were able to generate over a third of all possible codons. As the number of mutants increases, one replicates ever more often identical codons. The statistical approach is an ideal experimental scheme to test whether large numbers of mutants very different from the observed wild type sequences would still work in a laboratory setting, as required by neo-Darwinian theory. For about the same effort of generating all possible codon alternatives in one three-residue study, one could carry out statistically meaningful tests involving ten different sets of three-residue positions.
Discussion
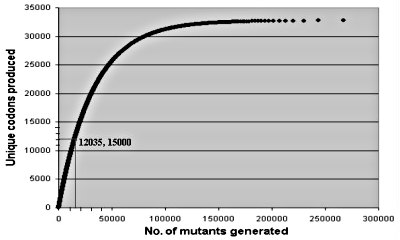
Figure 1. Average number of random trials needed to generate unique sets of three codons.17 15,000 trials generate about 12,035 different sets; 326,843 trials would be needed to generate all (32) possibilities.
Suppose that all possible amino acid variants were to be generated at the three residue positions of Experiment 3. Then, as pointed out above, we would expect about 2.7 times more viable mutants to be found in total. Let us apply this extrapolation factor to the number of mutants reported in Table 4 (2.7 x 5; 2.7 x 6; and 2.7 x 7). Many would conclude, that there should be about 14 x 16 x 19 = 4256 functional mutants differing by three amino acids from the wild type. We generously accepted this assumption in an earlier paper.6 However, extrapolation from the actual experimental data here indicates there would only be about two or three. The error is based on the assumption of mutational context independence.
To illustrate how significant this overestimation can be, let us consider a 150-residue protein, which is considerably smaller than an average sized protein, using 4256 vs. 3 alternatives as just calculated. We compare the likelihood of obtaining a suitable DNA sequence which provides a protein of minimal function upon which natural selection could act. The potential underestimation factor between these two probabilities is about that of guessing correctly that the sun will arise tomorrow morning vs. being able to guess two atoms in the whole universe in a row.16 Furthermore, the larger the protein, the more severe this assumption becomes.
The mathematics of information theory which Yockey used, and the alternative methods we provided8 for cytochrome c, contain this assumption. Therefore, the proportion of functional protein sequences we estimated is in all likelihood many orders of magnitude too generous towards the evolutionary model.
A second point we shall now consider, is that the functionality of the protein mutants reported17 drops dramatically when multiple mutations are present.
Table 5. Partitioning of possible mutants in categories according to number of codons available per amino acid at the three residue positions in Experiment 3.17
| Coding pattern [1] | No. of codon sequences in the pattern [2] | No. of amino acid sequences in the pattern | ||
|---|---|---|---|---|
| Calculation | No. | Calculation [6] | No. | |
| {3;3;3} | 1x[(9)3] | 729 | 1x[(3)3] | 27 |
| {3;3;2} | 3x[(92)(10)] | 810 | 3x[(3)2(5)] | 135 |
| {3;3;1} | 3x[(92)(12)] | 972 | 3x[(3)2(12)] | 324 |
| {3;2;2} | 3x[(92)(10)2] | 900 | 3x[(3)(5)2] | 225 |
| {3;2;1} | 6x[(9)(10)(12)] | 1080 | 6x[(3)(5)(12)] | 1080 |
| {2;2;2} | 1x[(10)3] | 1000 | 1x[(5)3] | 125 |
| {2;2;1} | 3x[(10)2(12)] | 1200 | 3x[(5)2(12)] | 900 |
| {3;1;1} | 3x[(9)(12)2] | 1296 | 3x[(3)(12)2] | 1296 |
| {2;1;1} | 3x[(10)(12)2] | 1440 | 3x[(5)(12)2] | 2160 |
| {1;1;1} | 1x[(12)3] | 1728 | 1x[(12)3] | 1728 |
| w/o Stop | 29791 [3] | |||
| Stop | (32)3-(31)3= | 2977 [4] | ||
| Total: [5] | 32768 | Total: | 8000 [7] | |
[1] {i;j;k} are the distributions of all possible codons; i is the number of synonymous codons which produce the same AA in the first position; j the second and k in the third position.
[2] The first number refers to how many permutations are possible by changing the position of the mutant AA among the three residue portions randomized. (No. of codons involved) x (No. of codons generating the same amino acid).
[3] Check: 31 of the 32 codons code for an AA: (31)3 = 29,791.
[4] Check: between one and three Stop codons could be generated among the three residue positions: 3 Stops: 1; 2 Stops: 3[4x4x2-1]; 1 Stop=3[4x4x2-1]2; total=1+93+2883=2977.
[5] Check: total number of codons is 32: (32)3 = 32,768.
[6] (Number of positional alternatives) x (number of different AA generated).
[7] Check: any of 20 alternative residues at each of three positions: (20)3 = 8000.
Climbing Mount Improbable
Any materialist theory for the origin of life on Earth needs to explain how the huge space of almost entirely non-functional polypeptides could be searched and the corresponding genes optimised within a few billion years. Neo-Darwinism requires that the earlier ‘boxes’, which represent the number of functional alternatives at specific portions of a protein, be vastly larger the earlier we are in the protein’s evolution. In Table 7 column 4 we see that the opposite was found here (see also Table 8 for the results from Experiment 1).
We pointed out above that the experimental design actually generates far more three-amino acid mutants than single ones. The fact that only one partially viable three-residue mutant was obtained implies a dramatic loss of protein functionality the more distant the sequence is from a wild type.
Why is this result surprising? Virtually all studies performed to test acceptable variability modify one residue at a time, since the number of multiple residue alternatives is huge. The need to identify all sequences and to test functionality would be overwhelming. The assumption of context independence is then made: anytime an amino acid is tolerated at a position, it is assumed to always be acceptable. We illustrate this assumption in Table 7 column 5, using the experimentally reported (i.e. not extrapolated) data. The number of sequence alternatives which differ by d amino acids from the wild type increases with the value of d, whereas the proportion of those biologically functional fails to increase yet more rapidly, as required by evolutionist theory.
This point did not escape the researcher’s attention: ‘In separate experiments, five of the seven core positions were altered individually. Only one to three amino-acid substitutions at each position yield a fully functional protein as is common for buried position’ (p. 33). What the authors probably did not suspect, however, is that subsequent research demonstrates this phenomenon is not limited to buried portions of proteins,18 as I plan to discuss in part two.
A critical point is that these kinds of laboratory experiments can generate multiple mutational changes at once, unlike step-by-step evolutionary theories. The designed shotgun approach can find unique combinations of compensatory residues which work. But in a naturalist scenario, once natural selection has committed itself to a choice at some point, improvement would be restricted to feasible paths from that starting point: all the alternative evolutionary routes are not available.7
Table 6. Number of codons able to generate mutant proteins differing by 0 to 3 amino acids (AA) from the wild type sequence.
| No. of AA differences from wild type [1] | Max. no. of different | Unique AA per unique codon [3] | Calc. no. different AA generated [4] | Functional mutants | ||
|---|---|---|---|---|---|---|
| Codons | AA [2] | Reported | Extrapolated [5] | |||
| 0 | 27 [6] | 1 | 0.037037 | 1 [13] | 0 | 1 [13] |
| 1 | 756 [7] | 57 | 0.075397 | 20.9 | 18 | 49 |
| 2 | 7,056 [8] | 1083 | 0.153486 | 397.8 | 4 | 11 |
| 3 | 21,952 [9] | 6859 | 0.312454 | 2519.4 | 1 | 3 |
| Stop | 2,977 [10] | 1261 [11] | 0.423581 | 470.2 | ||
| Total | 32,768 [12] | Total: | 1.00 | 3408.3 | ||
[1] The viable codons will all differ by zero to three residues from the wild type; or include Stop codon(s).
[2] Assuming all (32)3 = 32,768 codons had been produced and tested. From Table 7, column 2.
[3] Column 3 / column 2.
[4] (Unique AA sequences / possible unique codons) x number of unique codons generated in the experiment = (column 3 / 32,768) x 12,036 (Note: 12,036 unique codons were generated
by the 15,000 trials according to algorithm (1) in the main text). Alternative reasoning leading to the same result: (column 3/column 2)(column 2/32,768) x 12,036.
[5] Correction factor for no. of functional mutants were all to be generated: (column 3)/(column 5) = 2.72. Extrapolation: (correction factor) x column 6.
[6] Any of three codons can generate Leu at each of three positions: (3)3.
[7] Three codons can generate a Leu at any of 2 residue positions and 28 codons a mutant at the 3rd residue. Three such permutations are possible: 3[(3)2(28)].
[8] 28 mutant codons can be placed at 2 residue positions, 3 coding for Leu at the last residue. There are three ways of doing this: 3[3x(28)2].
[9] From Table 3: the 32 codons are distributed as: 3 generate the wild type amino acid L (Leu); 1 produces a Stop codon; therefore, any of the remaining 3 generate the wild type amino acid L (Leu); 1 produces a Stop codon; therefore, any of the remaining 28 codons can generate mutants in Experiment 3 at each position: (28)3.
[10] From Table 5.
[11] One to three Stop codons could be generated: 3[(20)2] + 3(20) + 1. Such truncated proteins are not functional.
[12] Confirmation: (32)3 = 32,768 codon alternatives. We have accounted for all possible codons.
Table 7. Number of mutant amino acid (AA) sequences predicted by context independence and those experimentally found. Results from Experiment 3.
| Differences from wild type [1] | Sequences possible | Experiment results | Assuming contact independence | ||
|---|---|---|---|---|---|
| Functional sequences [2] | Proportion functional [3] | Number | Proportion [4] | ||
| 0 AA | 1 | ||||
| 1 AA | 57 [5] | 18 | 3.16 x 10-01 | 18 [8] | 3.16 x 10-01 |
| 2 AA | 1083 [6] | 4 | 3.69 x 10-03 | 107 [9] | 9.88 x 10-02 |
| 3 AA | 6859 [7] | 1 | 1.50 x 10-04 | 210 [10] | 3.06 x 10-02 |
| Sum: | 8000 [11] | ||||
[1] Number of residues which differ from the wild type genome in the 3 amino acid region studies.
[2] From Table 4.
[3] Column 3 / column 2.
[4] Column 5 / column 2.
[5] Any of 19 residues except Leu generate a mutant; these can be placed at any of three residue postions. The remaining two residues must be the wild type Leu: 19 x 3.
[6] Any of 19 residues can be distributed pairwise among the three available residue positions: 3 x [(19)2].
[7] 19 alternatives can be placed in any of 3 residue position: (19)3.
[8] Number of alternatives, one per residue position: 5 + 6 + 7.
[9] Each of the residue alternatives found at each of the three positions could be present with one of the other: (5 x 6) + (5 x 7) + (6 x 7).
[10] Five alternatives in the first position, six in the second, seven in the third: 5 x 6 x 7.
[11] Check 20 alternatives possible in 3 positions: (20)3.
Testing Dawkins’ Weasel Model7 specifically
Suppose the whole protein under consideration has evolved by neo-Darwinian means, except for the three residues at positions Leu18-Leu57-Leu65. Let us defer the question as how it might have gotten this far, since no functional variants more than three residues distant from the wild type were obtained for the seven amino acid region studied. The data shown in Table 4 offers only one experimental starting candidate, AMI, which could evolve into LLL (see Figure 2). AMI was found to be ‘partially functional’ under artificial laboratory conditions. With little if any chance of surviving under natural conditions, we have a precarious starting point at best.
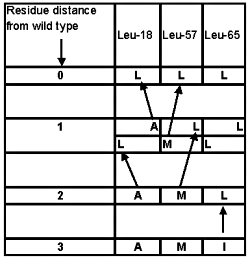
Figure 2. Feasible evolutionary paths for Experiment 3.17 Alternatives were identified as being at least partially functional in a laboratory setting.
Now, the rest of the protein must be conserved as the organism waits for a useful amino acid (‘AA’) modifying mutation at precisely one of these last three positions. Dawkins assumed in his ‘Weasel computer program’ that any letter lined up to match the target would immediately provide survival advantage. But the experimental data disproves this assumption. Figure 2 illustrates the difficulty. For AMI to move one residue closer to the target of LLL there are three sequence paths: LMI; ALI; and AML. However, only one of these, AML, was found. Furthermore, this single evolutionary intermediate is also only functional under artificial, induced laboratory conditions!
We have no evidence that a protein with now everything in place except the two AML residues could mutate to a different, fully functional protein which is still two-AA removed from the wild type: no other fully functional two-AA mutants (A_L or _ML, see Table 4) were obtained in Experiment 3. The single intermediate option, AML, at best barely functional, would have no measurable selective advantage and must avoid degradation or elimination until just the right future mutation occurs.
Of all the 18 single-AA functional mutants found, only two are feasible along this evolutionary path; ALL or LML (i.e. the intelligently designed shotgun approach to generating mutants can produce some functional alternatives which are, however, not accessible to step-by-step trial and error evolutionary attempts).
Point mutations are on the order of 1 out of 108 to 1011 replicated base pairs.19–20 The necessary mutations must occur precisely at the right place. This would require an unfathomable number of attempts, and during such time this and the other genes would be degraded. It is well known that very little DNA of not immediate use is found in bacteria, for several reasons.21
Now suppose such a protein had been well designed for a particular function from the very start. Sequence randomisation by non-lethal random mutations could subsequently produce additional variants which differ at a few residue positions.
The neo-Darwinian theory, however, is unworkable for two reasons:
New gene families must possess enough functionality throughout the entire evolutionary path at the whole organism level to permit natural selection to occur.
Should it be theoretically possible to find a path of functional intermediates connected by simple, random mutations, the chances of improvement is negligible every step of the way and the number of undesired alternatives which can be generated is much too great.
The data from Experiment 1 (Appendix 4) and Experiment 217 are more difficult to analyse. To a good approximation, all or almost all the data which arose from Experiment 1 led to the summary shown in Table 8, which reinforces the conclusions of this paper for a different portion of the same protein. Table 8 shows that the number of mutants three residues distant from the wild type is less than for one- and two-residue distance, and far lower than context independence predicts.
In fact, the overall trend seen in Table 2 is easy to discern after summing all functional and partially functional sequences. The number of viable variants which differ by one residue from the wild type is > by two residues > by three residues >> by four residues even though the proportion generated randomly lies orders of magnitude in the opposite direction. Greater mutational distance is clearly accompanied by rapid loss of protein functionality.
Amino acids differ in important chemical and physical properties, such as size, polarity, hydrophobicity, aromaticity, electronic charge and bonding geometry (e.g. proline, which can serve as a ‘helix-breaker’). Here and there individual residues could be substituted by a similar amino acid, but the same mutations would be severely damaging when several are present concurrently. In their final folded state, various regions of proteins must fulfill different requirements. The details are often understood in fine detail by biochemists:
For example, the active site of an enzyme must provide a suitable geometric and electrical environment to facilitate bringing the substrates into the transition state topology along the reaction path. Substitution by an amino acid of similar characteristics, such as size, might be possible at several locations, but multiple substitutions would destroy the reactive site. Often specific parts of proteins must interact with other proteins or biomolecules in precise ways. Limited modification at these locations is generally acceptable.
Amino acid sequences can also serve as informational signals for various purposes, such as to define where a protein is to be sent. This signal may still function after a few mutations, but not too many.
Sometimes part of a protein must provide a very hydrophobic region to cause a specific part to be embedded within a membrane: a few mutations may be acceptable individually, but several of these at the same time would render the protein useless.
We are left with an unworkable materialist theory as to how an original gene family may have arisen. But many cellular functions involve complex protein machines which require up to dozens of different, precisely meshed members to work together. These must be located correctly within the cell and in the right proportions. I have not discussed here the irreducible complexity22 issue: the requirement that many suitable proteins be found concurrently before any biological use (and therefore natural selection) would be possible.
Table 8. All acceptable alternative found from Experiment 1.17 V=Val; M=Met; Number of Amino Acid (AA) differences from wild type sequence.
| 1-AA | ||
|---|---|---|
| V-36 | M-40 | V-47 |
| I | L | I |
| A | V | T |
| C | A | |
| L | ||
| T | ||
| 2-AA | ||
|---|---|---|
| V-36 M-40 |
V-36 V-47 |
M-40 V-47 |
| CL | LI | LI |
| IV | IT | AI |
| LI | MI | AL |
| LL | ML | AI |
| LV | TI | CI |
| TL | CM | |
| IC | ||
| II | ||
| LA | ||
| LT | ||
| VI | ||
| 3-AA |
|---|
| V-36 M-40 V-47 |
| ICI |
| ILI |
| CLI |
| IAI |
| IVL |
| LLI |
| LLL |
| LVI |
| MLI |
Acknowledgements
I wish to thank the referees for the considerable effort that went into examining this paper and several anonymous suggestions.
Appendix 1—Contribution of variants at position Leu-18 in Table 4 from Experiment 20
In my analysis I imply that the alternative residues in Table 4 were generated only by Experiment 3.23 However, Experiment 2 could also produce mutants at the Leu-18 location. This contribution can be neglected to a first approximation, by calculating the expected number of contributions which may have arisen from Experiment 2.
Here are the facts we must take into account.
The number of different codon sets for the 4-residue portion of the protein studied in Experiment 2 is (32)4 = 1,048,576.
Not all 1,048,576 different codons could be produced by the 40,000 random variants generated. Using equation (1), Appendix 3 shows that about 39,247 unique codon sequences resulted.
-
The number of mutants which differ by one residue from the wild type at the Leu-18 position is calculated as follows. Leu can be coded by 3 codons and there is a Stop codon, leaving 32 - 3 - 1 = 28 alternatives possible; Val-37 and Val-47 can each be coded by any of 2 codons; Phe-51 by only 1 codon. Therefore, (28)(2)(2)(1) = 112 possible sequence alternatives.
Expected number of variants generated which differ by only one residue from the wild type, and specifically at Leu-18: 39,247 x 112/(32)4 = 4
However, it is likely that far less than 4 mutants actually show up in our data set for one-mutation in Experiment 3 (Table 4). Here are the reasons:
Of the total 92 surviving colonies in Experiment 2, only 30 unique sequences were actually identified. A third of 4 brings us down to about one.
The mutant(s) may already be represented among the sequences generated in Experiment 3.
Therefore, to a reasonable approximation we can consider virtually all of the 18 single residue variants in Table 4 as having been generated by Experiment 3.
Appendix 2—Reasoning behind algorithm (1) and the computer program shown in Appendix 3
For a specific portion of a protein, there is a total of n different candidate sets of codon possibilities. A limited number of trials are available to generate all possible sets. We assume for ease of understanding that each trial is performed sequentially. The first mutant will be unique. The second one might reproduce the first one, but has probability (n-1)/n of generating a different sequence. Therefore, on average n/(n-1) trials would be needed to generate another distinct mutant. The third attempt has a probability (n-2)/n of producing something new, and on average requires an additional n/(n-2) trials to provide another unique codon set.
A recursive relationship can be discerned. Yj is the average number of trials needed to generate j unique codon sets.
y1 = 0 + n/n
y2 = y1 + n/(n-1)
y3 = y2 + n/(n-2)
y4 = y3 + n/(n-3)
…
yj = yj-1 + n/(n-j+1)
as shown in equation (1).
The recursive relationship is run to see how large yj becomes for the available number of trials.
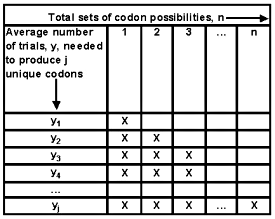
Figure 3. Number of random trials needed to generate j distinct codon sets.
Note: Once a codon set has been generated (one or more X cover that portion of the sequence), there remains one fewer new alternatives for the succeeding mutant trials.
Appendix 3—Java class to calculate number of unique DNA sequences generated by a limited number of mutational trials. See protocol used as published17
class Unique
{
int calc(int Codons, int Trials)
{
int j = 0;
double Yj1 = 1;
double Yj = 0;
double n = Codons;
while(Yj<=Trials)
{
Yj = Yj1 + (n/(n-j+1));
Yj1 = Yj;
j = j + 1;
}
return j;
}
public static void main(String[] args)
{
int Trials = 15000;
int Codons = 32768; // (32)**3
// int Trials = 40000;
// int Codons = 1048576; // (32)**4
Unique unique = new Unique();
System.out.println(‘Unique codons generated by: ‘ + Trials + ‘ trials: ‘ + unique.calc(Codons, Trials));
}
}
Appendix 4—Evaluation of the results from Experiment 1
Since the authors did not report which data in Table 2 arose from which experiment,24 analysing the results from Experiment 1 is not worth detailed statistical effort here. Some of the amino acid mutants may have come from Experiment 2 since Val-36 and Val-47 are involved in both experimental sets.
In Experiment 1, 20,000 mutants were generated which is a statistically significant portion of the (32)3 codon alternatives possible, from which 102 sequences were analysed (with identical amino acid sequences being found occasionally).
Most of the 40,000 mutants generated in Experiment 2, out of (32)4 codon alternatives possible, would have involved variants which differ by three or four codons from the wild type and therefore not show up in the data shown in Table 8 as having arisen from Experiment 1. Furthermore, only 30 of the colonies from Experiment 2 were sequenced anyway (Table 3).
These and more detailed analysis (not reported here) persuade us, that essentially all the single-mutants in Table 8 can be attributed to having arisen from Experiment 1, and reinforce the conclusions reached in this paper.
References
- Ubiquitin protein consists of 76 amino acids. It is part of a process to degrade proteins which are misfolded or contain abnormal amino acids, in a proteasome (which consists of a large number of different proteins). Additionally, three enzymes are necessary to attach ubiquitin molecules to a lysine side chain of the protein to be broken down (Lodish et al., Ref. 3, pp. 67, 504; Alberts et al., Ref. 4, p. 219). Yeast and human ubiquitin differ at only 3 of 76 residues (Alberts et al., Ref. 4, p. 942).
‘For example, the sequence of histone H3 from sea urchin tissue and of H3 from calf thymus are identical except for a single amino acid, and only four amino acids are different in H3 from the garden pea and that from calf thymus’ (Lodish et al., Ref. 3, p. 321).
The H4 protein consists of 102 residues. The sequence between cow and a pea differ by only two amino acids (Lodish et al., Ref. 3, p. 342).
- Lodish et al., Molecular Cell Biology, 4th Edition, W.H. Freeman and Company, New York, 2000.
- Alberts et al., Molecular Biology of the Cell, 3rd Edition, Garland Publishing, 1994.
- Stryer, L., Biochemistry, 4th Edition, W.H. Freeman and Company, New York, 1999.
- (a) Ref. 8, p. 119: ‘iii) Yockey assumed all residues theoretically tolerable would be mutually compatible.’
- Truman, R., Dawkins’ Weasel Revisited, TJ 12(3):358–361, 1998. In discussing Dawkins’ computer ‘Weasel’ program, I pointed out some assumptions made: p. 359, ‘5. Each setting is independent of the others and does not affect the probability of other required matches from occurring subsequently. 6. The order successful matching occurs is not relevant.’
- Truman, R. and Heisig, M., Protien families: chance or design, TJ 15(3): 115–117, 2001.
Besides the results from recent cassette mutagenesis studies (which we are now discussing) which contradict this view, there are two additional objections.
- A cytochrome c variant of lower functionality implies a very small selectivity factor, such as s < 0.001. Descendents of the mutant must survive for a very large number of generations, or the evolutionary attempt is lost. The vast majority of such low quality genes would not fix in the population.
- Survival in a natural setting is affected by many factors. Natural selection cannot automatically pinpoint a minimally advantageous point mutation from amongst the more than a thousand genes most free-living organisms have. Non-deadly mutations would surely accumulate over hundreds of millions of years. By now, a wide range of cytochrome c variants would have been generated and identified in current organisms.
Experimental details: seven key amino acids in the core of the N-terminal domain of a phage λ-repressor gene were varied by cassette mutagenesis in three experiments.
The plasmids were transformed into E. coli. Functional mutants of the gene, available to the host only via the plasmids, provide resistance to phage λ KH54. Since the great majority of the bacteria produced nonfunctional protein, they did not survive. The few survivors reproduced and formed large clonal colonies which could be visually identified and isolated. This experimental strategy decreased the number of mutants which needed to be sequenced by many orders of magnitude. Such a protocol is precisely what I was looking for: a technique by which vast numbers of alternative protein structures could be generated to test the proportion which are functional.
- I contacted the authors in the hope this data would be available. Professor Saur is still at M.I.T. and Professor Lim at the University of California at San Francisco.
- For Experiment 3, 35 or 36 of the survivors’ mutant genes were sequenced (Table 3).
- From Table 4: any of five mutated residues were found to be acceptable at position Leu-18, each of which would be compatible with any of six different residues at position Leu-57, each of which could be associated with any of seven residues at position Leu-65.
- The mutations induced can generate any of the 32 different codons shown in Table 1. These code for all possible 20 biological amino acids at the ribosomes.
- An Excel spreadsheet and a Java class were used, leading to the same results. The Java program also showed that on average 326,843 samples would have to be generated to produce all (32)3 codon alternatives.
- There are (20)3 = 8000 alternatives for our ‘box’ consisting of three residue positions. As an illustrative extrapolation for a 150-amino acid protein, the assumption of mutational contextual independence predicts a functional proportion of (4256/8000)50 = 2x10-14 whereas the experimental results only about [(3/8000)]50 = (5x10)-172. The ratio of these proportions is 2.5x10-158. The number of atoms in the universe is estimated to be around 1080 and the probability the sun will rise tomorrow is close to 1. I am not claiming that the ratio of 3/8000 from Experiment 3 is representative over the whole of this or other proteins.
- Lim, W.A. and Sauer, R.T., Alternative packing arrangements in the hydrophobic core of λ repressor, Nature 339:31–36, 1989.
- Axe, D.D., Extreme functional sensitivity to conservative amino acid changes and enzyme exteriors, J. Mol. Biol. 301:585–595, 2000.
In bacteria the mutation rate per nucleotide has been estimated to be between 0.1 and 10 per billion transcriptions:
- Fersht, A.R., DNA replication fidelity, Proceedings of the Royal Society (London) B212:351–379, 1981.
- Drake, J.W., Spontaneous mutation, Annual Reviews of Genetics 25:125–146, 1991.
For organisms other than bacteria, the mutation rate is between 0.01 and 1 per billion:
- Grosse, F., Krauss, G., Knill-Jones, J.W. and Fersht, A.R., Replication of ΦΧ174 DNA by calf thymus DNA polymerase α: measurement of error rates at the amber-16 codon, Advances in Experimental Medicine and Biology 179:535–540, 1984.
- Spetner, L., Not By Chance! Shattering the Modern Theory of Evolution, The Judaica Press, Chapter 4, 1998.
- Mira, A., Ochman, H. and Moran, N.A., Deletional bias and the evolution of bacterial genomes, Trends in Genetics 17(10):589–596, 2001.
- Behe, M.J., Darwin’s Black Box: The Biochemical Challenge to Evolution, Touchstone, New York, 1996.
- From Table 2 it is apparent that all single-residue mutants at positions Leu-57 and Leu-65 could only have come from Experiment 3. The changes at position Leu-18 could have come from Experiment 2 or Experiment 3. From the numbers available in the original paper I deduce that the following proportion of protein sequences of the surviving mutants were determined: for Experiment 1: 102/266; Experiment 2: 30/92; for Experiment 3: 35/36 as shown in Table 3.
- The purpose of the project was to see whether analysis of the acceptable amino acids at each position would permit deductions about the folded structure at this portion of the protein.

Answers in Genesis is an apologetics ministry, dedicated to helping Christians defend their faith and proclaim the good news of Jesus Christ.
- Customer Service 800.778.3390
- © 2024 Answers in Genesis
