Misconceptions About General Relativity, Cosmology, and the Big Bang

Just as all ideas have consequences, incorrect ideas can have very bad, or even dangerous, results. For instance, if our apologetics rely upon an easily refuted misconception, then those apologetics are suspect. If we argue against a theory quite sincerely but with misconceptions, then our argument is greatly diminished. The argument would amount to a sort of straw man attack, even though we may be honest in our attitude.

There are many misconceptions and misunderstandings about the big bang, cosmology, and modern relativity theory. Therefore it is helpful to discuss some of the common misconceptions about these topics in this chapter.

The Redshift Is Not a Doppler Shift

In describing the expansion of the universe, most treatments compare the redshifts of universal expansion to Doppler shifts. The Doppler shift is named for Christian Doppler, who discovered the principle in 1842. This phenomenon occurs with all waves, such as sound waves from a car horn. If the horn of an approaching car is sounded, adjacent sound waves will be crammed closer together so that we encounter more waves per second than if the car were not moving with respect to us. More waves per second correspond to an increase in frequency. Since our ears detect frequency as pitch, the increased frequency results in higher pitch than what we would hear from a stationary car. If the car is moving away from us, the waves are stretched so that we encounter a lower frequency, and we hear a lower pitch. If the car remains motionless and the listener moves toward or away from the car instead, then the pitch is increased or decreased in a similar fashion.

The light from stars can be Doppler shifted as well. If we move toward a star or it moves toward us, all of the star’s light will be shifted toward shorter wavelengths. Light is perceived as color, the shorter wavelengths being toward the blue end of the spectrum. Therefore we say that the star’s light is Doppler shifted toward the blue. On the other hand, if a star moves away from us or we move away from the star, the star’s light is Doppler shifted toward longer wavelengths, and we say that the star’s light is shifted toward the red. With either a blue or red Doppler shift, the entire spectrum of the star is shifted. The spectra of stars contain dark absorption lines. (please see the appendix for an explanation of how spectral lines are formed). Due to the Doppler effect, spectral lines will be slightly shifted from the wavelengths that they usually have. The amount of Doppler shift is measured by the displacement of these lines, and the amount of relative velocity can be calculated using an equation called the Doppler formula.

A star’s Doppler motion is a combination of our motion through space and the star’s motion. Through careful analysis of the Doppler motions of thousands of stars, astronomers have been able to determine roughly what our motion through space is. In turn, we have been able to measure the motions of individual stars in space. For instance, we know that the sun is moving nearly 250 km/sec as it orbits the center of the galaxy. We have found that stars generally follow one of two very different kinds of orbits around the galaxy, and these two types of orbits manifest themselves as different speeds. There are other subtle differences between these two groups of stars, which has become the basis of stellar population types.1

It is very easy to visualize the expansion of the universe as matter flying apart in space; so most books on the subject use the Doppler shift as the explanation of what is happening. This is most unfortunate, because this is not what is actually happening. Cosmologists usually assume that all matter in the universe is at rest with respect to space. What is expanding is space itself. Therefore, as space expands, the matter in the universe is carried along with the expansion. As such, particles are not actually moving apart. Instead, more space appears between particles as the universe expands.

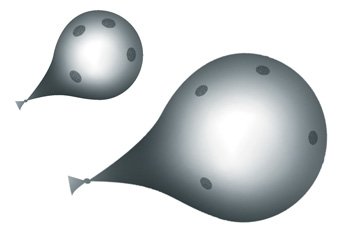
Image courtesy of Bryan Miller

A balloon is often used as a two-dimensional example of the expanding universe.

A balloon is often used as a two-dimensional example of the expanding universe. If dots are placed on the balloon with a marking pen, the dots will appear to move apart as the balloon is blown up. However the dots will grow in size with the expanding balloon, which is not what objects in the universe do. A better analogy is to glue sequins on the balloon. The sequins will appear to move apart, but the sequins themselves will not increase in size as the balloon expands. Notice that the sequins are not actually moving, but simply appear to move apart as they are carried along by the expansion of the balloon. In like fashion, galaxies can be at rest with respect to space, but they appear to fly apart due to the expansion of space. Therefore the redshifts due to the expansion of the universe are not Doppler shifts. Sometimes the perceived motion due to expansion is called Hubble flow.

This may seem like a minor distinction, but missing this very subtle point can lead to major misunderstandings. For example, the spectrum of the Andromeda Galaxy (M31) is blue shifted. Some ask how this can be, if the universe is expanding. Virtually all galaxies are in fact moving through space, rather than being at rest as in the very simple view mentioned above. What is the source of this motion? In most cases it is probably due to local gravity. Galaxies tend to clump together into clusters containing anywhere between a few dozen to a thousand galaxies. Our galaxy is a member of an assembly of about 30 galaxies called the Local Group, which happens to lie near the much larger Virgo Cluster. Clusters of clusters may form larger structures called super clusters.

All of these structures are presumably held together by gravity, which would imply that the various objects making them up have orbits. These orbital motions produce relative motions that are indeed Doppler in nature. Therefore the spectrum of any particular galaxy will have shifts due to the Doppler effect and Hubble flow at the same time. Since there is no way to observationally distinguish the two, we cannot say for sure how much of each exists. M31 is so close to us that its Hubble flow would amount to no more than 50 km/sec. Its gravitational motion greatly exceeds this, so the Doppler effect dominates the spectral shift of M31. The Doppler motion of M31 happens to be toward us. A few other galaxies show blue shifts, and they are all very close to us as well.

The mixing of Hubble flow and Doppler motion presents a problem in measuring the Hubble constant. To accurately measure the Hubble constant, we must sample galaxies that have large Hubble flows as compared to their Doppler motions. Doppler motions should be independent of distance, but Hubble flow must be proportional to distance (this is the Hubble relation). Nearby galaxies can best have their distances measured, but their shifts are dominated by Doppler motion. More distant galaxies have spectral shifts that are dominated by Hubble flow, but their distances are more difficult to measure accurately. Separating the two effects requires that we make certain assumptions and handle the data in particular ways. Part of the disagreement over the value of the Hubble constant in recent years has resulted from different approaches in handling this problem.

A Few Blueshifted Galaxies are Not a Problem for the Expanding Universe

As mentioned in the previous section, the Andromeda Galaxy has a blueshift rather than a redshift. This means that this galaxy is moving toward us rather than away from us. Some think that this is a problem for an expanding universe, thinking that in an expanding universe all galaxies must have redshifts. However, motions of nearby galaxies due to local gravity can overtake the expansion of the universe. Note that this can be true only of nearby galaxies. If a distant galaxy were to be found to have a blueshift, that would be a problem for the expanding universe.

On a related issue, about half the stars within our galaxy have redshift, while the other half have blueshift. Some people think that any object with a blueshift is a problem with an expanding universe. However, the effect of universal expansion is extremely small on the local scale. For instance, people on the other side of the earth are not getting farther from you because of expansion. Local effects, primarily gravity, overcome the extremely feeble universal expansion. Within our galaxy, gravity is the dominant force that holds the galaxy together. The blueshifts and redshifts that we observe in stars within our galaxy are due to Doppler shifts resulting from the orbits of the sun and the other stars around the galaxy. So this is not a problem for an expanding universe.

Inflation Does Not Contradict the Prohibition of Faster-Than-Light Speed

As previously discussed, physicists believe that faster-than-light speed is not possible. Because of mass increases with increasing speed, a particle that has mass would have infinite mass at the speed of light. Therefore, to accelerate a particle to the speed of light, an infinite amount of energy would be required. Since we do not have an infinite amount of energy at our disposal, no material particle can travel with the speed of light, though the speed may be arbitrarily close to the speed of light.

Because of this speed limit imposed upon matter, many people think that the faster-than-light expansion of inflationary cosmologies is not possible. If the expansion of the universe were due to Doppler motion, then this would be a problem. However, as discussed earlier, Hubble flow and Doppler motions are different. During an episode of inflation, particles do separate much faster than the speed of light, but that separation is not due to the motions of the particles through space, but by the rapid stretching of the space between the particles. This is a good example of how misunderstanding a concept can lead to erroneous conclusions.

Interstellar Reddening Is Not the Same as a Redshift

Like other spiral galaxies, the disk of the Milky Way contains a huge amount of dust. Dust particles are called grains, and are typically about 0.1 micron in size. Dust grains are probably made of a variety of substances, including silicates, carbon, iron, and ices. Dust tends to clump, so that there are regions in the disk of the galaxy that are pretty dust free, while other regions are extremely dusty. As starlight passes through dust, the grains scatter the light. The size of dust grains favors the scattering of shorter wavelengths (blue) of light more than longer wavelengths (red). The solid particles in cigarette smoke are about the same size, so that they also scatter blue light more effectively. That is why cigarette smoke appears blue when illuminated by strong light. Molecules in the earth’s atmosphere preferentially scatter sunlight in much the same way to produce the familiar blue sky.

When light is scattered, it is removed from the transmitted light. Some of the red light is scattered, but not as much as blue light is. Therefore, if light that has undergone scattering is observed, it will appear both fainter and redder. This is the reason why the rising or setting sun appears much dimmer and redder than the sun does high in the sky. At those times the light from the sun is entering the earth’s atmosphere at a grazing angle so that it passes through much more air than when the sun is higher in the sky. More air results in more scattering, making the sun appear simultaneously fainter and redder. Starlight undergoes much the same thing. The light from more distant stars generally must pass through more dust than the light from nearer stars, so more distant stars appear fainter and redder than they normally would. The reddening of starlight is called interstellar reddening, and the dimming of starlight is called extinction. In calculating distances of astronomical bodies, a correction for extinction must be applied.

Some people confuse interstellar reddening and redshift. The redshift changes all wavelengths of light by the same relative amount. The shape of the spectrum, often closely approximating what is called a blackbody, is preserved. All spectral lines are shifted by the same relative amount, which allows us to measure the amount of redshift. Interstellar reddening does not shift wavelengths—all spectral lines remain at where they normally would occur. The entire spectrum is depressed, and since the blue end of the spectrum is depressed more than the red end, the shape of the spectrum is altered.

The Redshift Does Not Usually Make Galaxies Appear Red

Some people have the impression that redshift makes galaxies appear more red in color. For most galaxies the redshift is so small that there is no appreciable change in color. Even for galaxies with large redshifts, the color of the galaxies will not be changed much. The reason is that although visible light from a galaxy is shifted to longer wavelengths and even into the infrared that the eye cannot see, that light is approximately replaced with normally invisible radiation in the ultraviolet that is shifted into the visible part of the spectrum. Therefore the spectrum of a galaxy has about the same shape as it would have if it had no redshift, and so the color is about the same.

With very large redshift, the color of a galaxy is altered so that the galaxy is redder than it normally would be, but the eye cannot detect this subtle color change. This color change can be determined by comparing the brightness of a galaxy at two different wavelengths, for instance in blue and yellow light. From the study of many nearby galaxies we have a good idea of what color a typical galaxy has. Very high redshift galaxies have systematically redder colors as determined with this method.

Hubble deep sky field

This process can be used to advantage in estimating redshifts. Taking photographs is a very efficient use of light, while spectroscopy is very inefficient. The difference occurs because with spectroscopy the light must be dispersed, or spread out. Observing time on very large telescopes is valuable, so we do not want to waste time measuring every galaxy for its redshift. Instead, in searching for distant galaxies we would like to select for spectroscopy those galaxies that likely have large redshifts. Measuring their colors may identify likely candidates for further study. Sometimes galaxies near the limit of detectability have been photographed, such as in the Hubble deep sky field. These galaxies are so faint that their spectra cannot be measured, but astronomers can estimate the amount of redshift from the colors. A correction must be applied, because astronomers expect that very distant galaxies are bluer than nearby galaxies. This is because astronomers assume that the light from very great distances originated when the sources were much younger. Galaxies in their youth are supposed to be dominated by blue light, because astronomers think that massive blue stars dominated the first generations of stars.

Modern Relativity Theory Does Not Eliminate the Concept of an Absolute Reference Frame

This is probably the most misunderstood aspect of modern relativity. Newton had formulated his laws with the assumption that there was some absolute standard of rest from which all motion could be measured. This eventually led to the development of the idea of aether, the stuff of space. Maxwell’s theory of electricity and magnetism developed in the 1860s suggested that light was a wave in this aether. The 1887 Michelson-Morley experiment was an attempt to measure the motion of the earth through the aether as it orbited the sun. The Michelson-Morley experiment was a null result, suggesting that the earth was not moving with respect to the aether or if you will, space. However, annually varying Doppler shifts in the spectra of stars as the earth orbited the sun strongly suggested that the earth was indeed moving. How this discrepancy could be explained remained a mystery for nearly two decades.

Albert Einstein pursued another explanation of the problem in his 1905 paper on special relativity. Einstein assumed that physical laws and the speed of light were invariant with speed. That is, no matter what one’s speed is, physical laws and the speed of light would be the same. Classical physics assumes that while physical laws are not changed by one’s speed, the observed speed of light should be the vector sum of one’s velocity and the velocity of light. Therefore if one measured the speed of an oncoming light beam as we moved toward the beam, the measured speed of light ought to be c + v, where c is the speed of light in the absence of our motion, and v is our speed. If on the other hand we are moving in the direction in which the light beam is traveling, we would expect to measure the speed of light to be c – v. The Michelson-Morley experiment revealed that the answer was c in either case. Einstein took this fact as a given.

With this novel, if not counterintuitive, assumption Einstein worked out the implications. He showed that as an object’s speed increases, its mass increases, its length decreases, and time in the reference frame of the moving object is slowed with respect to a reference frame that is not moving. Each of these effects has subsequently been confirmed with numerous experiments, mostly dealing with fast-moving elementary particles. For instance, unstable elementary particles that rapidly decay last longer when moving at high speeds. Another example is the observed increase in the masses of particles in particle accelerators. The mass increases limit the highest speeds that can be attained with a type of particle accelerator called the cyclotron.

The early success of special relativity was hailed as the end of the aether. Many scientists at the time claimed the concept of absolute space was no longer tenable. Even an early quote by Einstein suggested that he shared this belief. A decade after his paper on special relativity, Einstein published his general relativity that addressed accelerated reference frames and provided a new theory of gravity. Special relativity had considered only constantly moving reference frames, so a new theory had to be developed to handle ones that were changing speeds. One consequence of his theory was that a constantly accelerated frame is not distinguishable from a gravitational field. This ultimately led to the new approach to gravity, as discussed in chapter 1.

The early rejection of the concept of the aether or an absolute reference frame gave rise to the twin paradox, another idea that is frequently mishandled. Suppose that there are identical twin brothers. At about age 20 one twin goes on a voyage to a nearby star system at nearly the speed of light, while the other remains back on earth. After 40 years have passed on earth, the astronaut returns. The twin that remained on earth is now 60 years old and is showing his age, but due to time dilation the astronaut has only experienced a few months aging and looks pretty much the same as when he left earth. The astronaut has moved at a high speed compared to his brother on earth and so time has passed more slowly.

The paradox comes in when one considers the reference frame of the astronaut. If all reference frames are equal, as is allegedly what relativity theory says, then from the reference frame of the astronaut, his brother on the earth is the one that has moved, not the astronaut. This would suggest that the twin on earth should have experienced less time than the astronaut did. In other words, each twin could claim that the other one did the moving and hence experienced time dilation. Since both twins could not have undergone time dilation, the twin paradox is thought by some to invalidate relativity theory.

If all we had was special relativity, then the twin paradox might be a serious problem. However, we do have general relativity, which addresses accelerated reference frames. The astronaut twin had to undergo four separate accelerations. The first was to achieve a high speed in the first place. The second was to slow down upon reaching his destination. The third and fourth would have occurred upon starting the return journey to earth and slowing down to arrive at the earth. Meanwhile the twin on earth experienced no accelerations relevant to the problem. How do we measure accelerations? Accelerations can be measured with respect to the sum total of the matter of the universe. Upon acceleration, someone can observe that his speed is changing with respect to distant massive objects such as stars and galaxies. The earth-bound twin does not see this effect of acceleration, while his astronaut brother does. Therefore we can unambiguously determine which twin does the moving, and the twin paradox dissolves away.

The ability to measure accelerations with respect to distant massive objects is called Mach’s principle. Mach’s principle applies to constant motion as well. While individual distant massive objects may have their own motions, the sum total of all the matter in the universe is believed to be at rest with respect to space. Therefore the sum total of matter in the universe represents a preferred standard of rest. Early in the 20^th century, some theorists stated the modern relativity theory demands that there is no preferred standard of rest, that is, that all non-accelerated frames of reference are equally valid. This idea has become a common popular belief. However, this is in direct conflict with Mach’s principle, a foundation of modern relativity theory. So contrary to those early pronouncements and the public’s conception, modern relativity theory does tell us that there is an absolute standard of rest. That standard of rest is the frame of reference that is at rest with respect to the sum of all distant objects. Keep in mind that general relativity holds that space is a thing. One could argue that space as understood by general relativity could be identified with an aether, albeit not in the form originally envisioned.

The Constancy in the Speed of Light Is Misunderstood

One of the foundations of special and general relativity is that the speed of light is a constant, regardless of the speed of the source or the observer. As discussed in the previous section, this is very different from what one might expect. Unfortunately, many people misunderstand this principle. When light enters a medium, such as glass, the speed decreases. To many people this seems to violate the principle that the speed of light is a constant. However, the constancy of the speed of light refers to the measured speed with regard to the motion of the source and observer. The speed of light has its greatest value in a vacuum, and all speeds in media are less than the vacuum speed. Within a medium, the constancy of the speed of light regardless of the motions of the source and observer is true.

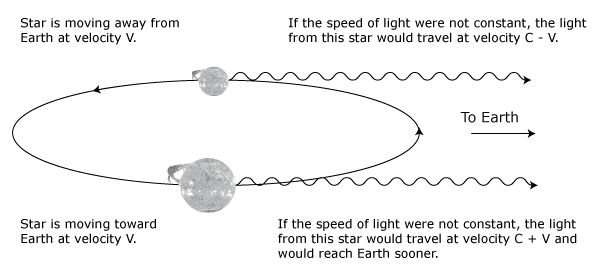
Image courtesy of Bryan Miller

A few years ago scientists measured the speed of light in a particular form of matter called a Bose-Einstein condensate to be a mere 17 m/sec. This speed is so incredibly slow that many people thought that this just had to violate the constancy of the speed of light, but this is not the case. Some asked if this means that light in some medium could travel faster than the speed of light in a vacuum. Theoretically this is not the case, and measurements of light speed in all media so far confirm that.

There have been experiments in recent years that have suggested to some physicists that the speed of light in some situations has been greater than the theoretical maximum of 300,000 km/s. These experiments and their interpretation have been very controversial. There are explanations that do not require supraliminal light speed. Until the physics community has fully digested this, it is not possible to discuss this issue further.

Acceptance of General Relativity Does Not Amount to Acceptance of Moral Relativism

Soon after the publication of Einstein’s theories of relativity early in the 20^th century, moral relativists seized upon the theories as support for their philosophy. They peddled the idea that all morals and standards were relative, so no standard could be held to be absolute. Moral relativists continued to spread the myth that Einstein’s theories of relativity proved that there were no absolute standards, but only relative ones. As shown in an earlier section, this assertion is patently false. Einstein himself did not like the name “relativity,” but instead called his theory, the “theory of invariance.” If anything, even special relativity alone posits that there is at least one absolute, the speed of light. A key foundation of general relativity is Mach’s principle, which states that there is an absolute standard of space against which all motions may be measured.

There is also the question of how a theory about the physical world could establish the basis of a system of morality. This is a gigantic leap of logic that was never demonstrated. The misappropriation of Einstein’s relativity theory by moral relativists ought to be opposed. Unfortunately, many Christians have allowed this fraud to continue or even unwittingly participated in it by arguing against relativity theory on similar philosophical grounds.

The Big Bang Was Not an Explosion

The name “big bang” is a misnomer. As mentioned in a previous chapter, Sir Fred Hoyle, who meant it as a term of derision, inadvertently coined the name. Unfortunately, to many people the name suggests an explosion. For instance, some critics ask the question, “What exploded?” To add to this, many popular accounts discuss the big bang as if it were an explosion. Explosions tend to be catastrophic events that lead to chaos and disorder, so the question is often asked how an explosion could have led to the order that we see in the universe. However, the only similarity between the big bang and an explosion is the sudden appearance of the universe and the resulting expansion of matter and energy. A true explosion would produce Doppler motion, but universal expansion is different from Doppler motion, as previously discussed.

For some time the model of the big bang has not been one of an explosion, so it is very important for critics of the big-bang theory that we correctly state the model so that we cannot stand accused of using a straw man argument. The universe is supposed to have begun in a high-temperature, high-density, but very uniform state. Uniformity is hardly the description of an explosion—an explosion should have introduced non-uniformity at its inception. Through expansion the density and temperature of the universe would have decreased to their current values. The uniformity of the measurements of light speed in all media so far universe must have been preserved through much of the expansion. The universe today is not uniform, so how did the universe develop non-uniformity? This is a bit of a problem for the big-bang model today, a topic that will be further explored in the next chapter.

The Universe Is Not Expanding into Anything

A frequent criticism of the expanding universe is to ask, “What is the universe expanding into?” The simple answer is that the universe is not expanding into anything. This misconception probably stems from the common analogy made to an expanding balloon, as discussed earlier in this chapter. As the balloon expands, spots on the balloon move apart. This two-dimensional analogy shows rather nicely how objects in the three-dimensional universe can get farther apart without actually moving. The rubber in the balloon is stretching in much the same way that space is stretching.

Unfortunately, this analogy fails as one considers the fact that a balloon obviously expands into adjacent space. Or put another way, the volume of the balloon increases at the expense of the volume of its surroundings. The universe is not expanding into anything; it is just getting bigger. Of course, one could claim that there are extra-dimensional realities outside of our universe into which space is expanding. However this sort of thing has no physical reality as far as we are concerned. Therefore extra-dimensional realities are not capable of being studied scientifically. Any consideration of such things would be a philosophical exercise at best. The claim that the universe must expand into something hardly constitutes a flaw in cosmology.

The Big Bang Did Not Begin at One Point in Space or in Time

A commonly held misconception is that while the big bang occurred at a finite time in the past, space and time are eternal. That is, space and time have always existed, and the big bang happened at some instant in time and some location in space. Most people visualize the big bang by first imagining that space was empty for a very long time before the big bang. They also pretend that if we had been present in the eternal empty space, we could have visualized that each of the three dimensions of space were number lines that intersected at one point. We could consider that point to be the origin of a three-dimensional Cartesian coordinate system. As we watched this very boring, empty universe for a long time, absolutely nothing happened. That is, until at some time the big bang suddenly appeared at the origin of the coordinate system. From its very hot, high-density beginning as a point, all of the matter and energy of the universe explosively expanded to fill space and eventually produced the universe that we see today, many of billions of years after the big bang.

While this is the common understanding of the big bang, it is completely wrong. First, according to the theory, the big bang was not an explosion of mass and energy into space in time, but rather it was an explosion of space and time as well. Not only did matter and energy come into existence at the big bang, but space and time did as well. There was no space before the big bang, but neither was there time. Sometimes people question the big bang by asking, “What was here before the big bang?” This is an improper question, because “here” was not here then. For that matter, “then” was not then then either. This may seem contradictory or silly, but carefully consider the consequences of space and time commencing with the big bang. The concept of “here” requires that space exist. If space does not exist, then “here” cannot exist either. The words “then” and “before” depend upon the existence of time. If time does not exist, then the concepts of “then” and “before” have no meaning. So the very term “before the big bang” is meaningless.

Our mode of thinking is so linked to causality and sequential events that it is difficult to understand what is meant by this. This may seem illogical to the layman, but this is the current concept of the big bang. Unfortunately, many people who do have a grasp of the big-bang theory fail to see the consequences of no time prior to the big bang. We shall explore this in another section.

One result of space originating in the big bang is that the big bang did not occur at one point or one location of the universe and then spread elsewhere. Instead, the big bang happened everywhere in the universe. The difference was that the universe was quite a bit smaller back then. Thus it is incorrect to imagine that the big bang happened at some point or location and then spread elsewhere into space. Nor can one ask where the big bang happened, for it happened everywhere.

Olber’s Paradox Has No Bearing on Modern Cosmology

In 1826, H. W. M. Olber developed an idea that squarely contradicted the cosmology of his time. Suppose that the universe is eternal and infinite and that stars uniformly inhabit it. In such a universe our view in every direction eventually would be blocked by stellar surfaces. The brightness of a star decreases by the inverse square of the distance, but the number of stars visible in this model increases with the square of the distance. These two factors exactly compensate, so that the sky in every direction should be as bright as a star, such as our sun. Therefore, the sky should be extremely bright, as bright as the sun. This expectation is in stark contrast to the observed darkness of the night sky. This has become known as Olber’s paradox, though apparently others, such as Edmund Halley, discussed the matter a century before Olber.

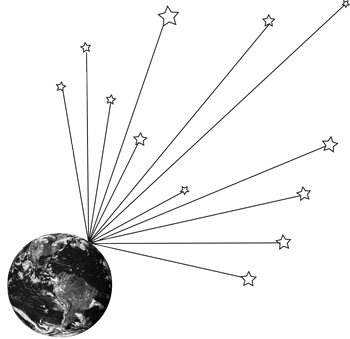
Image courtesy of Bryan Miller.

Olber’s paradox states that our view in every direction eventually would be blocked by stellar surfaces.

Some creationists have used Olber’s paradox to argue against the big bang and other evolutionary or atheistic cosmologies. However, how relevant is this objection? Let us examine the assumptions that lead to Olber’s paradox and some of the suggested resolutions to the paradox. The first assumption is that the universe is infinite. Some attempted resolutions claim that general relativity does not allow for an infinite universe, but this is not true. The solutions to Einstein’s equations allow for finite and infinite solutions, though many prefer the finite ones. The second assumption is that stars are uniformly distributed in the universe. That is obviously not true on any local scale, for stars are arranged in galaxies and galaxies tend to clump into clusters and super clusters. However, on a large scale this clumping appears less important. For comparison, we believe that the matter around us consists of many clumps called atoms, but for most purposes we can assume that objects are made of continuous distributions of mass. In the same fashion the universe may appear continuous on a grand scale. The third assumption is that the universe is eternal. With the big-bang model, the universe has a finite age, and this appears to be the best route for resolving Olber’s paradox within the big-bang model. Before expounding on this, let us discuss some of the other suggested, but flawed, resolutions of Olber’s paradox.

Within our galaxy and many other galaxies there is a huge amount of interstellar dust. This dust absorbs the light of more distant stars. Along the plane of the Milky Way the obscuration is so great that our view of distant stars is completely blocked. One suggestion is that interstellar dust absorbs so much of the light from stars that the night sky is dark. The problem with this resolution is that as the dust absorbs light, it is heated. In the infrared part of the spectrum we can see radiation due to the heat of this dust. With time, the dust temperature should increase so that eventually the dust ought to be nearly as bright as stars. Therefore, in an eternal universe this does not solve the problem.

Another suggested resolution is that redshift moves radiated energy from the visible into the infrared part of the spectrum, so that the amount of visible light is diminished. I was once taught this in an astronomy class. The problem with this is that the redshift also moves energy normally in the ultraviolet into the visible. Therefore, as energy is moved out of the visible part of the spectrum, other energy takes its place. Thus this explanation fails to account for the dark sky as well.

As already mentioned, the key to resolving Olber’s paradox is to examine the assumption of an eternal universe. In the time that Olber’s paradox was discovered, scientists had long assumed that the universe was eternal. In the 20^th century the acceptance of the big-bang theory convinced most scientists that the universe had a beginning and hence has a finite age. If the universe is, say, 15 billion years old, then we cannot receive light from anything more distant than 15 billion light years. It is as if we are located at the center of a spherical, finite universe that is 15 billion light years in radius. As far as the amount of light is concerned, it does not matter if the universe is finite or infinite, because we cannot see objects beyond 15 billion light years, a large, but finite distance. Given that the observable universe is finite, our view is not blocked by the surfaces of stars in every direction. In most directions we can see beyond all stars. Thus Olber’s paradox is not a problem in a big-bang universe. The only relevance that Olber’s paradox has today is in the context of an eternal universe, which is still supported by only a few adherents.

The Big Bang Does Not Prove God’s Existence

As discussed in the introduction, since the time of the ancient Greeks until well into the 20^th century many scientists assumed that the universe was eternal. One result of the big-bang theory is that it has convinced most scientists that the universe had a beginning. In a book written in 1978, the astronomer Robert Jastrow2 pointed out that for the first time in history, mainstream science and the Bible agreed on the finite age of the universe. While Jastrow is an agnostic, he found it fascinating that modern science has begrudgingly come into agreement with the Bible on this one issue. Many contemporary Christian apologists go beyond Jastrow and argue that the big-bang model is in perfect agreement with the biblical account of creation, and furthermore that the big bang shows that God must exist.3 There will not be a full discussion here of whether the big-bang model is compatible with the Bible. We will do that in the next chapter. Here we will explore the legitimacy of using the big bang to argue for God’s existence.

The argument for God’s existence using the big bang relies upon of the principle of causality. Causality means that any event that occurs (an effect) has some cause. Let A be a cause or agent that directly results in some event B. Then logically one can say that A causes B. A is the cause, and B is the effect. All effects in turn become causes of new effects, and so forth. At any time there are countless chains of cause and effect that are parallel and intertwined with one another. Conversely every effect must have a cause. Logicians and philosophers have long recognized that in the distant past there may have been an “uncaused cause.” That is, there was a cause that was not the effect of an earlier cause, and from which all subsequent cause and effect relationships descended.

Of course many would identify the uncaused cause as God. However, in an eternal universe there would be no need of an uncaused cause, because cause and effect would have been operating over all time. This avoidance of an uncaused cause may have been the appeal that the eternal universe had in Western thought. As some Christian apologists point out, the big-bang theory posits that the universe had a beginning, so that an infinite chain of cause-and-effect relationships is no longer tenable. Jastrow would agree with this, but he would disagree on the identity of the uncaused cause. Christians would certainly identify the uncaused cause as the God of the Bible. Jastrow would insist that the big bang was the uncaused cause.

If A causes B, then B must occur after A does, for no effect can precede its cause. It is also doubtful that an effect and its cause can occur simultaneously. The approach of the Christian apologist is to argue that if B is the big bang, then the only cause, A, available is God, because nothing physical can precede the big bang. But this reveals a fundamental lack of understanding of the big-bang model, or causality, or both. Smith4 makes this point in his discussion of the equations that give rise to the big bang. These equations relate physical qualities (space and time) of the universe. It is very clear that these equations suggest (or demand?) that time did not exist before the big bang. To ask a question such as “what was here before the big bang?” makes no sense, as discussed in an earlier section in this chapter. Time began with the big bang, and the big bang was the first event in time. Therefore the big bang had no antecedent. If time did not exist before the big bang, then any extrapolation of a temporal principle, such as the causality principle, past the beginning of time is unwarranted. Thus an appeal to causality to argue for God’s existence is completely illogical. This does not mean that God does not exist, of course. It merely means that appeal to causality will not demonstrate His existence if the big bang were true.

Apologists generally attempt to sidestep this difficulty a couple of different ways. One way is to suggest that there is some extra-dimensional causality principle that works beyond our universe of which our causality principle bound by time is only a part. This is an appeal to a hypothetical principle that cannot be demonstrated, and hardly constitutes a good proof. Another approach is to argue for simultaneous cause and effect. If time began with the big bang, then an eternal God certainly would exist at the same time that the universe came into existence and thus could be shown to be the cause of the universe. The analogy is made to a soft cushion lying under a heavy weight, such as a bowling ball. The weight depresses the cushion, but can one say whether the weight causes the depression or whether the weight and the depression occur simultaneously? Physics clearly tells us that indeed the weight causes the depression in the pillow. That would seem to settle the matter as to what is the cause (the weight) and what is the effect (the depression). However some would respond that that is true in a finite situation, but would it be warranted in a situation where the weight and pillow were eternally existent? That question cannot be answered with confidence with either physics or logic. However to raise such an issue is grossly inconsistent with what is being argued. The entire point of the big bang-based apologetic is that the universe had a beginning. How then can one then invoke an eternal situation to support the line of reasoning for God’s existence using a non-eternal universe?

In summation, the use of the big bang to prove God’s existence requires the use of the causality principle. However a cause must precede its effect. If the universe, via a big bang, is the effect, then its cause, God, must precede the big bang in time. The correct view of the big-bang model is one in which time began with the big bang. The big bang had no antecedent. Therefore the use of the causality argument across the boundary of time at the beginning of the universe is an unwarranted extrapolation. This does not argue against God’s existence—it merely means that we can conclude nothing about His existence with this kind of argument.

As discussed in the previous chapter, much current research in cosmology is an attempt to explain how the universe could have come into existence in a fashion that is consistent with the physical laws that we observe within the universe. Since the universe had a beginning, there must be some uncaused cause. The theist will conclude that the uncaused cause is God. However the atheist or agnostic could just as well conclude that the big bang is the uncaused cause. Either conclusion appears to be valid. The atheist or agnostic could claim that his position has more validity, because the theist attempts to invoke two uncaused causes, the big bang and a deity.

Some Christian apologists today who accept the big-bang claim that the big-bang theory has caused many professionals in the field of cosmology to realize that there must be a Creator and thus have been led to the God of the Bible. This claim is misleading at best in that while there may be a few cosmologists and those who have written with some authority in cosmology who may have turned to Christ as a result of their studies, the vast majority have not. We have previously discussed the fact that Robert Jastrow (author of God and the Astronomers), while impressed with certain elements allegedly common to the Genesis and the big bang, remained an agnostic. In an interview Alan Guth was asked that if the universe could come from nothing (via his inflation model), what does that mean to us as human beings? Guth replied, “I think it undermines the belief that we are here for a any cosmic purpose. It does not mean that our lives are meaningless. It means we must give meaning to our lives ourselves.” This is hardly consistent with a biblical world view.

Or consider the words of Steven Weinberg, author of the immensely popular book, The First Three Minutes5:“Ever since people started thinking systematically about the world, there’s been a widespread impression that the universe exists partly to serve the interests of humanity. I don’t think that’s true…. The effort to understand the universe is one of the very few things that lifts human life a little above the level of farce and gives it some of the grace of tragedy.” This, too, is antithetical to biblical Christianity or even to a personal God of any kind. In his very readable book, Before the Beginning,6 Martin Rees does not raise the issue of God, but he does not have to, when one considers that his suggestion that we live in an immense “multi-verse” containing an infinite number of universes is an attempt to explain how we and our apparently improbable big-bang universe could exist. It is obvious that in Rees’s view there is no need for a Creator.

Perhaps some Christian apologists are confused by the fact that some cosmological researchers and writers even use the word “God” in some of their popular writings. For instance, Paul Davies has gone so far as to put God’s name in the titles of two of his books dealing with cosmological questions (God and the New Physics7 and The Mind of God8). Stephen Hawking uses the word “God” frequently in his best-selling book, A Brief History of Time.9 However, anyone who carefully reads either of these two gentlemen will quickly find that neither one of them uses “God” to refer to anything remotely resembling the biblical God. Instead, they use God to mean an impersonal imposition of order (via natural law) upon the universe. Most researchers admit that they do not know how this order arises so that it does have a sort of mystical property, but suspect that the laws of nature probably reside in matter rather than space. There is a nearly universal hope that this mystery too shall fall with further work. In short, rather than being turned to the true and living God by their science, most modern cosmologists are engaging in a patently atheistic enterprise.

The Universe Does Not Have to Have a Center

The geometry that most people study is Euclidian geometry. Euclidian geometry is called this because its basic postulates were formulated by Euclid more than two millennia ago. Two-dimensional Euclidian geometry is sometimes called plane geometry, for the two dimensions lie in a plane. Also we could call plane geometry flat, because a plane is flat, meaning it has no curvature. In a plane, parallel lines do not intersect. Suppose that in a plane you have a line and a point not lying on that line. Then one, and only one, second line may be drawn through the point parallel to the first line. This is the fifth of Euclid’s five postulates. This reasoning may be applied to a third dimension to produce solid Euclidian geometry. This, too, is a flat geometry.

Most people assume that the universe is flat, but is it? What is a non-flat, or non-Euclidian geometry? Go back to Euclid’s fifth postulate. If that postulate is not true, then there are two possibilities. One possibility is that there are no parallel lines. The other possibility is that there is more than one line passing through a point parallel to another line. While both of these may seem strange, both are very real possibilities and have applications. The situation where there are no parallel lines is found on the surface of a sphere. It should be obvious that the surface of a sphere is not flat, so you should begin to see the difference between flat and curved geometries.

Image courtesy of Bryan Miller

Many people think that the universe must have a center. If the universe is flat and finite, then it must have a center, but if the universe is infinite it will not have a center. However there are other possible geometries that may not require a center. The easiest example to consider is a finite universe that is curved back onto itself. Such a universe would have no boundary, or edge, yet one could travel indefinitely in one direction. A two dimensional analogue is the surface of the earth. Locally the earth’s surface appears flat, because the radius of curvature is so large. One could travel forever in one direction, but of course that would require passing through one’s starting point countless times. Does the earth’s surface, or for that matter the surface of any sphere, have a center? Notice that I did not ask if the sphere had a center; I asked if the surface of the sphere has a center. Geometrically, the answer is of course no. In like fashion, if three-dimensional (spatial) space is finite and closes back upon itself, then there can be no special point that we can call the center. In reality we do not know the nature of space enough to say if the universe has a center or not, though it is much easier to visualize a space that has no center.

The CBR Cannot Be Caused by Dust or Starlight

As stated in chapter 1, the CBR is an impressive prediction of the big-bang model. The CBR is real, so one cannot deny its existence. Therefore if one wishes to replace the big-bang model, one must present a credible explanation for the CBR. Alternate explanations have been offered. Recent creationists and proponents of the steady-state theory have both proposed that dust is responsible for the CBR. The universe contains much dust, dust being microscopic solid particles. Dust particles may be made of various substances, such as silicates, ice, and iron. When exposed to starlight, dust particles will absorb energy and experience a temperature increase. Any object at a temperature above absolute zero (which is to say all objects) radiates energy. If an object has a temperature of 3K, then it will radiate with a blackbody curve having a peak in the microwave part of the spectrum very much like the CBR. Therefore uniformly distributed dust at a uniform temperature of 3K would produce the CBR.

However there are several problems with this explanation. First, dust is not uniformly distributed. In the Milky Way Galaxy dust is found very close to the galactic plane, and even within the galactic plane dust is very clumpy. In other spiral galaxies we see that dust is similarly distributed as in our galaxy. Given that dust is not homogeneously distributed, thermal radiation from dust should be very inhomogeneous, unlike the very smooth CBR. A second problem is that all dust clouds are at a much higher temperature than the CBR. Indeed, astronomers have found much emission from interstellar dust, but at a blackbody temperature much closer to 100K than 3K. In the far infrared part of the spectrum the galactic plane is very bright due to dust emission. One could counter that the CBR is the collected emission from dust in very distant sources and hence redshifted to the point that the observed temperature is much cooler than what was emitted. The problem with this solution is that galaxies are so clumped that we ought to see localized warm spots in the CBR due to large clusters of galaxies. As mentioned earlier, the CBR is so smooth as to be an embarrassment for the standard cosmology, but this solution fits the data even more poorly.

A similar appeal to greatly redshifted starlight as the source of the CBR is sometimes made. The reasoning is that the combined light of the many stars in countless galaxies at tremendous distances is blended together to appear homogeneous and is redshifted so much that the radiation corresponds to a 3K blackbody. The second argument against dust as the source of the CBR applies here as well. There is no evidence, despite its assumption, that the visible matter in the universe is homogeneous at any level. Even if there were homogeneity at some distant level, one would expect some foreground superclusters of galaxies to produce enough excess radiation to cause noticeable hot spots in the CBR. This is not seen.

The Cosmological Constant Is Not a Fudge Factor

Sometimes the cosmological constant, Λ, is called a fudge factor. This stems from a misunderstanding of what Λ means physically and from a poor understanding of the history of the use of Λ. The history is that Einstein introduced Λ in his solution to the general relativity equation to produce a static universe. When we later discovered that the universe was expanding, Λ was revoked, but was more recently reintroduced to solve some potential problems with the standard model. Critics often ridicule the possibility of a non-zero Λ on the basis that it would act as some sort of anti-gravity, despite any experimental evidence of its existence.

If that were all that there was to it, the introduction of Λ would indeed be arbitrary. However, Einstein was quite justified in introducing Λ. The equations being solved are differential equations, a discipline that has wide application in many areas of science. The solution to any differential equation will have some constant of integration. The value of the constant is determined by the conditions placed upon the solution. The conditions are called boundary conditions, or, if the constant is determined by the values of some quantities at the start of the problem, they are called initial conditions. Often the constant of integration has zero value, but not always. The cosmological constant is such a quantity. Many think that Λ should be zero, but the possibility exists that it is not. Its value is determined by boundary conditions of the universe, but we do not know what those boundary conditions are. Every constant of integration has some physical meaning that is obvious from the nature of the problem. The meaning of Λ is that it is a repulsion term. Therefore Einstein solved the most general case (non-zero Λ), and then set Λ according to what he thought the boundary conditions of the universe were. This was a proper and legitimate thing to do, though it apparently was not the correct boundary value.

Checking Your Understanding

1. Are redshifts of galaxies due to the Doppler effect?
2. Can galaxies have a blueshift in an expanding universe?
3. What is the twin paradox? How is it resolved?
4. How can inflation cause things in the universe to separate faster than the speed of light, if things cannot travel faster than the speed of light?
5. Do redshifted galaxies appear red?
6. What does it mean that the speed of light is a constant?
7. Why is the “big bang” a bad name for the standard cosmological model?
8. What was here before the big bang?