
Chapter 2
More Recent Developments in Cosmology
Since the 1970s many exciting things have been happening in cosmology. This article is a discussion of various cosmological ideas.
Until the 1960s, many people did not take cosmology seriously. While the musings of cosmologists were fascinating, they remained just that for lack of definitive data. The situation began to change with the discovery of the CBR in 1964. In the wake of that discovery, additional relevant data began to be found, and many new theories were developed. One of the more peculiar ideas was the realization that particle physics had much to tell us about cosmology. The peculiarity comes from considering the intimate relationship between the study of the smallest things (particle physics) and the largest thing (cosmology). Since the 1970s many exciting things have been happening in cosmology.
What follows in this chapter is a discussion of various cosmological ideas, in which it may often appear as if the author agrees with these ideas or with the big-bang theory. We should emphasize that this is only for the sake of discussion. In a later chapter we will see how the big-bang cosmology and related ideas discussed here are in conflict with the creation account in the book of Genesis. To discuss these concepts for now it is easiest to treat them as if they are acceptable, setting aside for a time the question of whether they are consistent with a biblical world view. In other words, we ask that you put on a “big-bang hat” to engage in this discussion. Please do not take from the discussion in this chapter that the author supports the big-bang model or that he has any enthusiasm for it.
The Rate of Expansion and the Flatness Problem
As the universe expands, the rate of expansion is slowed by the gravity of matter in the universe. An analogy can be made to an object that is projected upward from the surface of the earth. The speed of the object will slow due to the earth’s gravity. For small speeds the object will quickly reverse direction and fall back to the earth. As the initial speed is increased, the object will move to higher altitudes before falling back to earth. There is a minimum speed, called the escape velocity, for which the object will not return to the earth’s surface. At the earth’s surface the escape velocity is about 25,000 mph. Theoretically, an object moving at escape velocity will eventually arrive at an infinite distance from the earth with no remaining speed. Objects moving faster than the escape velocity will never return, but they will never come to rest. Space probes to the moon or other planets must be accelerated above the escape velocity. The more that their speeds exceed the escape velocity, the shorter time their trips will take.
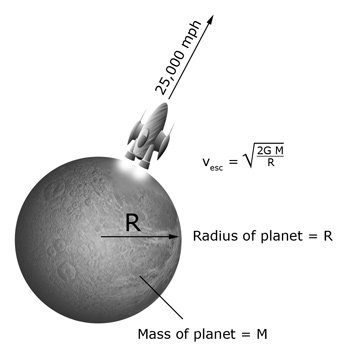
Image courtesy of Bryan Miller
Escape velocity of a spaceship
The universe should behave in a similar way. If the expansion is too slow, gravity will eventually reverse the direction so that the universe will contract once again. This presumably would lead to a sort of reverse of the big bang that is usually called the “big crunch.” This would also result in a finite lifetime for the universe. If the expansion exceeds some value akin to the escape velocity, the expansion will be slowed, but not enough to reverse the expansion. In this scenario the universe will expand forever, and as it does its density will continually decrease.
The escape velocity of the earth depends upon its mass and size. In a similar fashion, the question of whether our universe will expand forever or contract back upon itself depends upon the size and mass of the universe. An easier way to express this is in terms of one variable (rather than two) such as the density, which depends upon both mass and size. There exists a critical density above which the universe will expand forever and below which it will halt expansion and collapse upon itself. If the universe possesses the critical density, its expansion will asymptotically approach zero and never collapse.
One of the parameters used to describe the universe is Ω (the Greek letter omega), defined to be the ratio of the total gravitational potential energy to the total kinetic energy. Gravitational potential energy is energy that an object possesses because of its mass and any gravity present. On the earth, some object with elevation has gravitational potential energy. Examples would include a car parked on a hill or water behind a dam. The higher the hill or the higher the dam, the more energy there is. The more powerful hydroelectric dams are those that are higher and have larger amounts of water behind them. As the water is allowed to fall from its original height and pass through a turbine, the gravitational potential energy is converted to electrical energy. Kinetic energy is energy of motion. A speeding bullet contains far more energy than a slowly moving bullet.
Since the universe has mass and hence gravity, it must have gravitational potential energy as well. The expansion of the universe represents motion, so the universe must have kinetic energy as well. As the universe expands, the gravitational potential energy will change. At the same time, gravity will slow the rate of expansion so that the amount of kinetic energy will change as well. Generally the two energies will not change in the same sense or by the same amount so that Ω will change with time. A value of Ω < 1 means that the kinetic energy is greater than the gravitational potential energy. Conversely, a value of Ω > 1 means that the gravitational potential energy exceeds the kinetic energy. If a big-bang universe began with Ω < 1, then Ω will decrease in value. The minimum value is zero. If on the other hand Ω > 1 at the beginning of the universe, then Ω should have increased in value. Therefore, over billions of years the value of Ω should have dramatically changed from its initial value. For several decades all data have suggested that while Ω is indeed less than 1, it is not much less than 1. The sum of all visible matter in the universe produces an Ω equal to about 0.1. The prospect of dark matter pushes the value of Ω closer to 1.
The fact that Ω is very close to 1 today suggests that the universe began with Ω almost, if not exactly, equal to 1. If Ω were only a few percent less than 1 initially, then the evolution of the universe since the big bang should have produced an Ω dramatically less (many orders of magnitude) than 1 today. How close to 1 did the value of Ω have to be at the beginning of the universe to produce the universe that we see today? The value depends upon certain assumptions and the version of the big bang that one uses, but most estimates place the initial value of Ω equal to 1 to within 15 significant figures. That is, the original value of Ω could not have deviated from 1 any more than the 15th place to the right of the decimal point. Why should the universe have Ω so close to 1? This problem is called the flatness problem. The name comes from the geometry of a universe where Ω is exactly equal to 1. In such a universe space would have no curvature and hence would be flat. There are several possible solutions to the flatness problem.
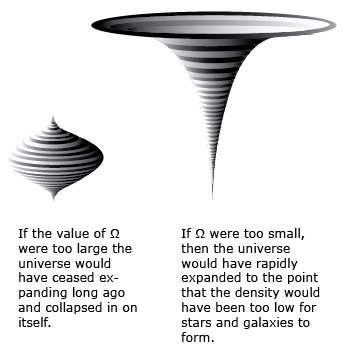
Image courtesy of Bryan Miller
One possible answer to the flatness problem is that this is just how the world happens to be. While this is not a physical impossibility, it does raise some troubling questions, at least for the atheist. It seems that the initial value of Ω could have been any number, but only a very small range in values could have led to a universe in which we exist. If Ω were too small, then the universe would have rapidly expanded to the point that the density would have been too low for stars and galaxies to form. Thus there could have been no planets and no life. Ergo, we would not have evolved to observe the universe. If on the other hand the value of Ω were initially too large, the universe would have ceased expanding long ago and contracted back to a “big crunch.” This would not have allowed enough time for us to evolve. Either way, we should not exist. Therefore the correct conditions that would have allowed our existence were present in the universe from the beginning.
The Anthropic Principle
Nor is the value of Ω the only feature of the universe fit for our existence. Scientists have identified a number of other parameters upon which our existence depends. Examples include the masses and charges of elementary particles, as well as the constants, such as the permittivity of free space, that govern their interactions. If some of these constants had slightly different values, then stable atoms as we know them would not be possible or the unique properties of carbon and water upon which life depends would not exist. All of these quantities are fundamental, that is, they do not depend upon other parameters, but are instead numbers that had to assume some values. There is no reason why those constants have the values that they have, other than the fact that they just do. Of all the random permutations of the constants that could have occurred, our universe exists as it does with these particular numbers. What is the probability that the universe would assume parameters that would be conducive to life, or even demand that life exist? To some it appears that the universe is designed; from its beginning the universe was suitable for our existence. In the early 1970s a scientist named Brandon Carter dubbed this line of reasoning the anthropic principle.1
To many Christians this constitutes strong evidence of God’s existence and has become part of their apologetics.2 Of course, use of the anthropic principle assumes that the big-bang cosmogony is correct. There is much difficulty in reconciling the big bang to a faithful rendering of the Genesis creation account, a topic that will be explored in a later chapter.
To atheists and agnostics the case is not nearly as clear. How do they resolve this issue? They try several approaches. One is to argue that the probability question has been improperly formulated. They maintain that one should ask what the probability of the existence of something is only before that something is actually observed. Once the object in question is known to exist, its probability that it exists with specified characteristics is 1, no matter how unlikely it may seem to us.
I can use myself as an example. If one considers the genetic makeup of my parents, it is obvious that there were literally billions of different combinations of children that my parents could have had. Each potential child would have had unique features, such as sex, height, build, and eye and hair color, to mention just a few. My parents only had two children, so it would seem that I am extremely improbable. Yet, when people meet me for the first time, they are not (usually!) amazed by my existence. Most people recognize that given that I exist, I must exist in some state. Therefore the probability that I exist as I do is 1. They argue that the incredible odds against my having the traits that I have only make sense if the probability were asked before I was conceived. In like fashion the universe exists, so the probability that it exists as it does must be 1. Therefore, they claim, we should not be shocked that the universe exists as it does.
How does one respond to this answer? We shall see in chapter 4 that a similar argument is used against the work of the astronomer Halton Arp, so the discussion there would apply here as well. We will repeat some of that here. We use probability arguments all of the time to eliminate improbable explanations. DNA testing is now used in many criminal cases. If there is a tissue sample of the perpetrator of a crime left at the scene of the crime, then DNA often can be extracted. The sample may be skin or blood cells, hair, or even saliva on a cigarette butt. Comparison of the DNA from the sample with DNA extracted from a suspect can reveal how well the two DNA samples match. Often this is expressed as how improbable it would be for two people selected at random to share the same DNA. If the probability were as little as one in a million, then that would be considered solid evidence of guilt to most people. However, a defense attorney may argue that as unlikely as a match between his innocent client and the truly guilty party is, the match actually happened so the probability is 1. That argument alone without any other evidence to exonerate the defendant is obviously very lame and would not convince any competent juror. Yet, this answer to Arp’s work asks us to believe a similar argument.
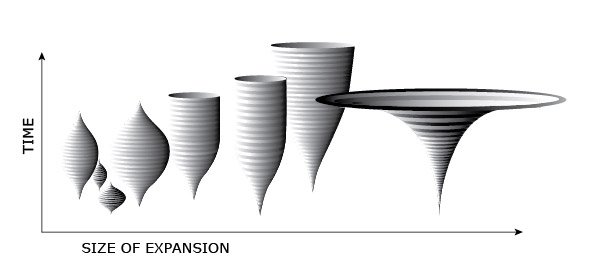
On the left of the illustration are those universes that collapsed back on themselves before life could begin and on the right are those universes that expanded too quickly and will continue to expand forever.
Image courtesy of Bryan Miller
There are other possible answers to the anthropic principle. For instance, some cosmologists suggest that our universe may not be unique.3 Our universe may be just one of many or even infinite universes. This concept of a “multi-verse” will be discussed further shortly. In this view each separate universe has its own unique properties, a few having properties that allow for life, but most being sterile. We could not exist in most of the universes, so it should not surprise us that we exist in a universe that is conducive for life. This explanation gets very close to the essence of the response to the anthropic principle discussed above. The only difference is that this answer seeks to explain our existence by appealing to a large sample size. The reader should note that this sort of answer is hardly scientific (how could it be tested?), and amounts to rather poor philosophy at best.
Inflation
Returning to the flatness problem, a radically different answer was pursued in the early 1980s. Late in 1979 Alan Guth suggested that the early universe might have undergone an early rapid expansion. According to this scenario, shortly after the big bang (somewhere between 10-37 and 10-34 seconds after the big bang) when the universe was still very small, the universe quickly expanded in size by many orders of magnitude (the increase in the size of the universe might have been from the size of an elementary particle to about the size of a grapefruit). This behavior has been called inflation. Inflation would have happened far faster than the speed of light. To some people this appears to be a violation of Einstein’s theory of special relativity, which tells us that material objects cannot move as fast as the speed of light, let alone faster than light. However, in the inflationary model objects do not move faster than the speed of light, but rather space expands faster than light and carries objects along with it. The initial value of Ω may have not been particularly close to 1, but as a result of inflation it was driven to be almost identically equal to 1. Therefore the universe was not fine-tuned from the beginning, but rather was forced to be flat through a very natural process. Inflation solves the flatness problem without invoking the anthropic principle as another potential difficulty.
Inflation can explain several difficulties other than the flatness problem. One of these is the homogeneity of the universe. The CBR appears to have the same temperature in every direction. If two objects that have different temperatures are brought together so that they may exchange heat, we say that they are in thermal contact. Once the two objects no longer exchange heat while still in thermal contact, they must have the same temperature and we say that they have come into thermal equilibrium. Regions of the universe that are diametrically opposite from our position and from which we are now receiving the CBR have yet to come into thermal contact, yet those regions have the same temperature. How can that be if they have not been in thermal contact before? This problem is often called the horizon problem, because parts of the universe that should not have come into contact yet would be beyond each other’s horizon. In an inflationary universe, very small regions of the universe could have come into thermal equilibrium before inflation happened. After inflation, the regions could have been removed from thermal contact until thermal contact was reestablished much later. With this possibility, widely dispersed regions had been in thermal equilibrium earlier, so it is not surprising that they are still in thermal equilibrium.
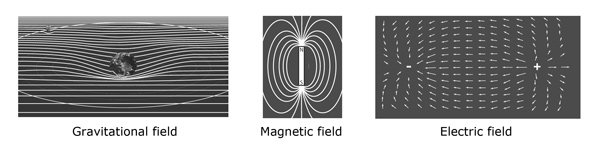
Image courtesy of Bryan Miller
Examples of fields
What mechanism drives inflation? Two classes of solutions have been suggested. One possibility is an energy field, called an “inflaton,” that fills the universe. Fields are used in physics to describe a number of phenomena. Examples of fields are gravitational fields that surround masses, electric fields around charges, and magnetic fields around magnets. Fields can be thought of as permeating and altering space. The release of the inflaton’s energy would have powered inflation.
An alternate suggestion is that inflation was powered by a process that is sometimes called “symmetry breaking.” There are four recognized fundamental forces of nature: gravitational force, the electromagnetic force, and the weak and strong nuclear forces. All observed forces could be described as manifestations of one of these fundamental forces. The history of physics is one of gradual unification of various, apparently disparate, forces. For instance, during the early and middle parts of the 19th century, a series of experimental results suggested that electrical and magnetic phenomena were related. A set of four equations formulated by James Clerk Maxwell unified electricity and magnetism into a single theory of electromagnetism. During the 1970s a theory that united electromagnetic forces with the weak nuclear force was established. In fact, Steven Weinberg, whose very famous popular-level book on the big bang, The First Three Minutes, shared the 1978 Nobel Prize in physics for his contribution in this unification. While the electromagnetic and weak nuclear forces have different manifestations today, the unification of these two forces into a single theory means that they would have been a single phenomenon at the much higher temperatures present in an early big-bang universe. With this unification we can say that there are now three fundamental forces of nature.
Most physicists believe that all the forces of nature can be combined into a single theory. Work is progressing on a theory that will unify all of the fundamental forces, save gravity. Gravity is believed to be hard to unify with the others, because gravity is so much weaker than the other forces. If and when such a theory is found, it will be called a grand unified theory (GUT). Physicists hope that one day gravity can be combined with a GUT to produce a theory of everything (TOE). Much research is dedicated to finding a GUT, and there are several different approaches to the search. Almost all involved agree that the unification of forces would only happen at very high energies and temperatures. This is why attempts at developing a GUT require the use of huge particle accelerators—bigger accelerators produce higher energies. Cosmologists think that the temperature of the very early universe would have been high enough for all of the forces of nature to be unified. This unity of forces represents a sort of symmetry. As the universe expanded and cooled, the forces would have separated out one by one. Being the weakest by far, gravity would have separated first and then been followed by the others. Each separation would have been a departure from the initially simpler state, introducing a form of asymmetry in the forces of nature. Therefore the separation of each force from the single initial force is called symmetry breaking.
Symmetry breaking is similar to a phase transition in matter. When ice melts, it requires the absorption of energy that cools the environment of the ice. Likewise when water freezes it releases energy into the environment. When symmetry breaking occurs, energy is released into the universe. This energy powers the inflation. Many cosmologists think that it is possible that the universe could undergo another symmetry-breaking episode with potentially cataclysmic results for humanity. Of course, without any knowledge of the relevant physics required, it is impossible to predict when or even if such a thing is likely.
Since its inception there have been thousands of papers written about the inflationary universe, and there have been more than 50 variations of inflationary theories proposed. Because inflation has been able to explain several difficult problems, it will probably remain a major player in big-bang cosmology for some time to come. Almost no one has noticed that there are no direct observational tests for inflation, its appeal being directly a result of its ability to solve some cosmological problems. The inflation model plays an important role in origin scenarios of the big bang, as we shall see shortly.
String Theory
Another new idea important in cosmology is string theory. String theory posits that all matter consists of very small entities that behave like tiny vibrating strings. In addition to the familiar three dimensions of space, string theory requires that there be at least six more spatial dimensions. This brings the total number of dimensions to ten, nine spatial and one time dimension. Why have we not noticed these extra dimensions? Since the early universe, these dimensions have been “rolled up” into an incredibly small size so that we cannot see them. Nevertheless, these dimensions would have played an important role in the behavior of matter and the universe early in its history. This introduces the relationship between cosmology and particle physics. The unification of physical laws presumably existed in the high energy of the early universe. Since the interactions of fundamental particles would have been very strong in the early universe, the proper theory of those interactions must be included in cosmological models.
Many popular-level books have been written on string theory. Even the Christian astronomer (and progressive creationist) Hugh Ross has weighed in with a treatise4 where he invokes string theory to explain a number of theological questions. What is easy to miss in all of these writings is that string theory is a highly speculative theory for which there is yet no evidence. It may be some time before this situation changes. Among cosmologists the tentative nature of string theory is recognized, and there are other possible theories of elementary particles.
Dark Matter
Galaxies tend to be found in groups called clusters. Large clusters of galaxies may contain over a thousand members. Astronomers assume that these clusters are gravitationally bound; that is, that the members of a cluster follow stable orbits about a common center of mass. In the 1930s the astronomer Fritz Zwicky measured the speeds of galaxies in a few clusters. He found that the individual galaxies were moving far too fast to be gravitationally bound, a fact since confirmed for many other clusters. This means that the member galaxies are flying apart and over time the clusters will cease to exist. The break-up time of a typical cluster is on the order of a billion years or so, far less than the presumed age of the clusters. Some creationists cite this as evidence that the universe may be far younger than generally thought. In other words, the upper limit to the age of these structures imposed by dynamical considerations might be evidence left by our Creator.
To preserve the antiquity of clusters of galaxies, astronomers have proposed that the clusters contain much more matter than we think. There are two ways to measure the mass of a cluster of galaxies. One is to measure how much light the galaxies in the cluster give off (luminous mass). Counting the number of galaxies involved and measuring their brightnesses give us an estimate of the mass of a cluster. Studies of the masses and total light of stars in the solar neighborhood give us an idea of how much mass corresponds to a given amount of light. The second way to estimate the mass is to calculate how much mass is required to gravitationally bind the members of the cluster given the motions of those members (dynamic mass). Comparison of these two methods shows that in nearly every case the dynamic mass is far larger than the luminous mass. In some cases the luminous mass is less than 10% of the dynamic mass.
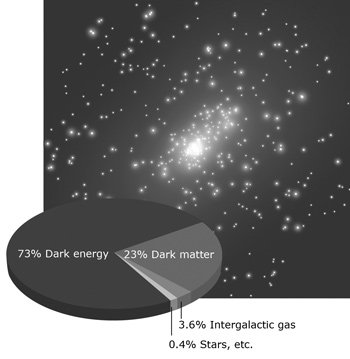
Image courtesy of NASA
If the dynamic mass calculations are the true measure of the masses of clusters of galaxies, then this suggests that the vast majority of mass in the universe is unseen. This has been dubbed dark matter. If this were the only data supporting the existence of dark matter, then suspicion of the reality of dark matter would be quite warranted. However, in 1970 other evidence began to mount for the existence of dark matter. In that year an astronomer found that objects in the outer regions of the Andromeda Galaxy were orbiting faster than they ought. This was unexpected. Gravitational theory suggests that within the massive central portion of a galaxy, from which most of its light originates, the speeds of orbiting objects should increase linearly with a distance from the center. This is confirmed by observation. However, theory also suggests that farther out from the central portion of a galaxy (beyond where most of the mass appears to be) orbital speeds should be Keplerian. Orbiting bodies are said to follow Keplerian motion if they follow the three laws of planetary motion discovered by Kepler four centuries ago. An alternate statement of Kepler’s third law is that orbital speeds are inversely proportional to the square root of the distance from the center. What was found instead is that the speeds of objects very far from the center are independent of distance or even increase slightly with distance. Similar behavior has been found in other galaxies, including the Milky Way.
This strange behavior for objects orbiting galaxies at great distances is independent evidence for dark matter, but it also tells where dark matter resides. If these objects are truly orbiting, then basic physics demands that much matter must exist within the orbits of these bodies, but beyond the inner galactic regions where most of the light comes. These outer regions are called the halos of galaxies. Since there is little light coming from galactic halos, this matter must be dark. Estimates of the amount of halo dark matter required to produce the observed orbits are consistent with the estimates from clusters of galaxies. Both suggest that, like an iceberg, what we see only accounts for about 10% of the mass.
What is the identity of dark matter? There have been many proposed theories. “Normal” matter consists of atoms made of protons, neutrons and electrons. The masses of the neutron and proton are very similar, but the mass of the electron is about a factor of 1,800 less massive than the proton or neutron. Protons and neutrons belong to a class of particles called baryons. Since most of the mass of atoms is accounted for by baryons, “normal” matter is said to be baryonic. We would be most comfortable with baryonic solutions to the dark matter question, but baryonic matter is difficult to make invisible. While faint stars are by far the most common type of stars and hence account for most stellar mass, low mass stars are so faint that the light of galaxies is dominated by brighter, more massive stars. However, even if dark matter consisted entirely of extremely faint stars, their combined light would be easily visible. If the matter were in much smaller particles such as dust, the infrared emission from the dust would be easily detected. Some have proposed that dark matter is contained in many planet-sized objects. This solution, dubbed MACHO (for MAssive Compact Halo Object), avoids the detectable emission of larger and smaller objects just mentioned. There has been an extensive search for MACHOs, and there is some data to support this identification though this is still controversial.
More exotic candidates for dark matter abound. Some suggest that dark matter consists of many black holes that do not interact with their surroundings enough to be detected with radiation. Another idea is that if neutrinos have mass, then large clouds of neutrinos in galactic halos might work. During the summer of 2001 strong evidence was found that neutrinos indeed have mass. Alternatively, heretofore-unknown particles have been proposed. One is called WIMPS, for Weakly Interacting Massive ParticleS. Obviously MACHO was named in direct competition with WIMPS. The identity of dark matter is another example of how cosmology and particle physics could be intimately related.
The relationship of dark matter to cosmology should be obvious. The fate of the universe is tied to the value of Ω, and Ω depends upon the amount of matter in the universe. If 90% of the matter in the universe is dark, then Ω could be very close to 1, and dark matter would have a profound effect upon the evolution of the universe over billions of years. The presence of dark matter would have been vitally important in the development of structure in the early universe. The universe is generally assumed to have been very smooth right after the big bang. This assumption is partly based upon simplicity of calculation, but also upon the unstable nature of inhomogeneities in mass. If the matter in the universe had appreciably clumped, then those clumps would have acted as gravitational seeds to attract additional matter and hence would have grown in mass. If those gravitational seeds were initially too great, then nearly all of the matter in the universe would have been sucked into massive black holes leaving little mass to form galaxies, stars, planets, and people. If, on the other hand, the mass in the early universe were too smooth, there would have been no effective gravitational seeds, and no structures such as galaxies, stars, planets, and people could have arisen. The range of homogeneity in which the initial conditions of the big bang existed and given rise to the universe that we now see must have been quite small. This is another example of the fine-tuning that the universe has apparently undergone that to some suggests the anthropic principle.
If dark matter exists, then its role in a big-bang universe must be assessed. Most considerations include how much dark matter exists and in what form. The dark matter may be hot or cold, depending upon how fast the matter was moving. If the dark matter moved quickly then it is termed hot. Otherwise it is cold. The speed depends upon the mass and identity of dark matter. It should be obvious that at this time dark matter is a rather free parameter in cosmology.
The COBE and WMAP Experiments
The early universe must have had some slight inhomogeneity in order to produce the structure that we see today. If there were no gravitational seeds to collect matter, then we would not be here to observe the universe. Cosmologists have managed to calculate about how much inhomogeneity must have existed in the big bang. This inhomogeneity would have been present at the age of recombination when the radiation in the CBR was allegedly emitted. The CBR should be very uniform, but the inhomogeneity would have been imprinted upon the CBR as localized regions that are a little warmer or cooler than average. Predictions of how large the inhomgeneities should be led to the design of the COBE (COsmic Background Explorer, pronounced KOB-EE) satellite. COBE was designed to accurately measure the CBR over the entire sky and measure the predicted fluctuations in temperature.
The two-year COBE experiment ended in the early 1990s with a perfectly smooth CBR. This means that temperature fluctuations predicted by models then current were not found. Eventually a group of researchers used a very sophisticated statistical analysis to find subtle temperature fluctuations in the smooth data. Variations of one part in 105 were claimed. Subsequent experiments that were more limited in scope were claimed to verify this result. These have been hailed as confirmation of the standard cosmology.
However, there are some lingering questions. For instance, while the COBE experiment was designed to measure temperature variations, the variations allegedly found were an order of magnitude less than those predicted. Yet this is hailed as a great confirmation of the big-bang model. Some have written that the COBE results perfectly matched predictions, but this is simply not true. Since the COBE results, some theorists have recalculated big-bang models to produce the COBE measurements, but this hardly constitutes a perfect match. Instead, the data have guided the theory rather than the theory predicting the data.
Another fact that has been lost by many people is that the alleged variations in temperature were below the sensitivity of the COBE detectors. How can an experiment measure something below the sensitivity of the device? The variations became discernable only after much processing of the COBE data with high-powered statistics. One of the COBE researchers admitted that he could not point to any direction in the sky where the team had clearly identified a hotter or cooler region. This is a very strange result. No one knows where the hotter or cooler regions are, but the researchers involved were convinced by the statistics that such regions do indeed exist. Unfortunately, this is the way that science is increasingly being conducted.
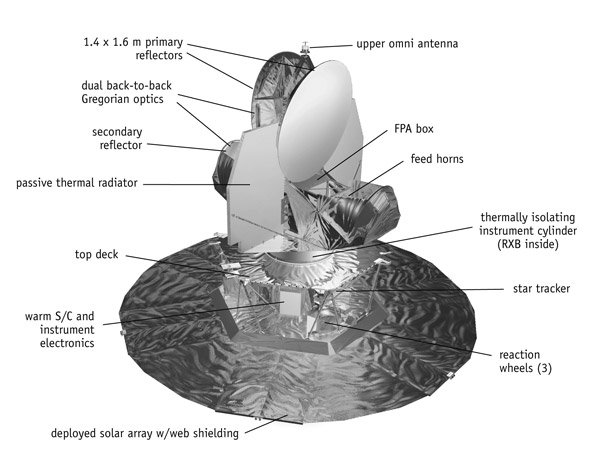
Image courtesy of NASA
WMAP (Wilkinson Microwave Anisotropy Probe)
To confirm the temperature fluctuations allegedly discovered by COBE, the WMAP satellite was designed and then launched early in the 21st century. WMAP stands for the Wilkinson Microwave Anisotropy Probe, and was originally designated MAP, but was renamed after David Wilkinson, one of the main designers of the mission, died while the mission was underway. WMAP was constructed to detect the faint temperature variations indicated by COBE, and WMAP did confirm those fluctuations. In early 2003 a research team used the first WMAP results along with other data to establish some of the latest measurements of the universe. This study produced a 13.7 billion year age for the universe, plus or minus 1%. It also determined that visible matter accounts for only a little more than 4% of the mass of the universe. Of the remaining mass, some 23% is in the form of dark matter, with the remainder 73% in an exotic new form dubbed “dark energy.” Dark energy will be described shortly.
The Hubble Constant
In the first chapter we saw that Hubble’s original measurement of H0 was greater than 500 km/sec Mpc, but that the value of H0 had fallen to 50 km/sec Mpc by 1960. The value of H0 remained there for more than three decades. In the early 1990’s new studies suggested that H0 should be closer to 80 km/sec. Astronomers who had for years supported the older value of H0 strongly attacked the new value, and so there was much conflict on this issue for several years.
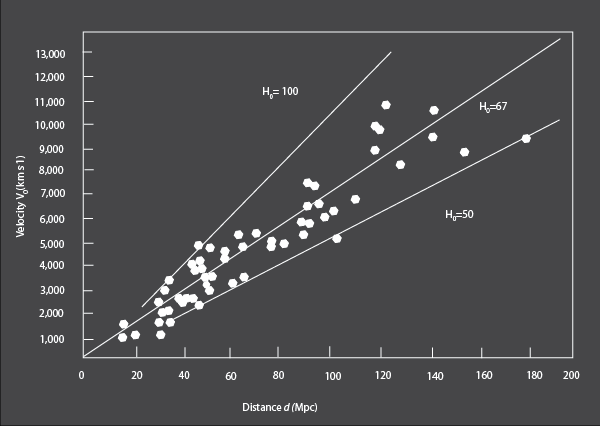
The Hubble constant describes how fast objects appear to be moving away from our galaxy as a function of distance. If you plot apparent recessional velocity against distance, as in the figure above, the Hubble constant is simply the slope of a straight line through the data.
Besides professional pride, what else was at stake here? Not only can the Hubble constant give us the distance of galaxies, it can be used to find the approximate age of the universe. The inverse of the Hubble constant, TH, is called the Hubble time, and it tells us how long ago the big bang was, assuming that Λ is zero and neglecting any decrease in the expansion due to the self-gravity of matter in the universe. Since the universe must have undergone some sort of gravitational deceleration, the Hubble time is an upper limit to the age of a big-bang universe. If you examine the units of H0 you will see that it has the dimensions of distance over time and distance so that the distances cancel and you are left with inverse time. Therefore TH has the units of time, but the Mpc must be converted to kilometers and the seconds should be converted to years.
For instance, a Hubble constant of 50 km/sec Mpc gives a TH of 1/50 Mpc sec/km. A parsec contains 3x1013 km, so an Mpc equals 3x1019 km. A year has approximately 3x107 seconds. Putting this together we get
TH = (1/50 Mpc sec/km)( 3x1019 km/Mpc)(year/3x107 sec) = 2x1010 years.
Therefore a Hubble constant of 50 km/sec Mpc yields a Hubble time of 20 billion years. Factoring in a reasonable gravitational deceleration gives the oft-quoted age since the big bang of 16 to 18 billion years.
Cosmic Strings
A brief mention should be made of cosmic strings, which must not be confused with the string theory of particles. Surveys of galaxies and clusters of galaxies show that they are not uniformly distributed. Instead, clusters of galaxies tend to lie along long, interconnected strands. If galaxies and other structures of the universe condensed around points that had greater than average mass and thus acted as gravitational seeds, then why are galaxies now found along long arcs? One possible answer is cosmic strings. Cosmic strings are hypothesized structures that stretch over vast distances in the universe. The strings are extremely thin but very long, and they contain incredible mass densities along their extent. Obviously cosmic strings are not made of “normal” matter. Cosmic strings were to act as gravitational seeds around which galaxies and clusters formed. There is yet no evidence of cosmic strings, and so this idea remains controversial.
Since the Hubble time is inversely proportional to the Hubble constant, doubling H0 would halve TH. The suggestion that H0 should be increased to 80 km/sec Mpc decreased the Hubble time to about 12.5 billion years. Gravitational deceleration would have decreased the actual age of the universe to as little as 8 billion years. This ordinarily could be accepted, except that astronomers were convinced that globular star clusters, which contain what are thought to be among the oldest stars in our galaxy, were close to 15 billion years old. Thus a higher Hubble constant would place astronomers in the embarrassing position of having stars older than the universe.
There were several possible ways to resolve this dilemma, and astronomers eventually settled upon a combination of two. First, the teams of astronomers who were championing different values for H0 found some common ground and were able to reach a consensus between their two values. At the time of the writing of this book (2003) the established value for H0 is 72 km/sec Mpc. This gives an age of the universe between 12 and 15 billion years, with the preferred value at the time of this writing as 13.7 billion years. Second, the ages of globular star clusters were reevaluated. We will not discuss how this was done in detail, but it involves properly calibrating color-magnitude diagrams of globular clusters. Calibration requires knowing the distance, and the Hubble Space Telescope provided new data that enabled us to more accurately know the distances of globular clusters. The recalibration reduced the ages of globular clusters to a range only slightly less than the new age of the universe. In the estimation of most cosmologists the uncertainty in both ages allows enough time for the formation of the earliest stars sometime after the big bang.
This episode does illustrate the changing nature of science and the unwarranted confidence that scientists often place in the thinking of the day. Before this crisis in the age of the universe and the ages of globular clusters, most astronomers were thoroughly convinced that both of these ages were correct. Anyone who had suggested that globular clusters were less than 15 billion years old would have been dismissed rather quickly. However when other data demanded a change, necessity as the mother of invention stepped in, and a way to reduce the ages of globular clusters was found. The absolute truth of the younger ages has now replaced the absolute truth of the older ages. What most scientists miss is that, apart from crises, the new truth would never have been discovered. We would have blithely gone on totally unaware that our “objective approach” to the ages of globular clusters had for a long time failed to give us the “correct” value.
The Return of the Cosmological Constant
As discussed in chapter 1, Einstein had given a non-zero value to the cosmological constant to preserve a static universe, a move that he later regretted. For some time Λ equal to zero came into vogue, and many cosmologists frowned upon any suggestion otherwise. Actually the idea of non-zero Λ never really went away. For instance, by the 1950s many geologists were insisting that the age of the earth was close to the currently accepted value of 4.6 billion years, but the Hubble constant of the day was far too large to permit the universe to be this old. Some cosmologists proposed that a large Λ had increased the rate of expansion in the past so that the corresponding Hubble time gave a false indication of the true age of the universe. Just as gravitational deceleration can cause the actual age of the universe to be far less than the Hubble time, an acceleration powered by Λ can cause the actual age of the universe to be greater than the Hubble time. In the mid 1950s the cosmological distance scale was revised in such a fashion that the Hubble constant was decreased to pretty much what it is today with a corresponding increase in the Hubble time so as to produce a universe much older than 4.6 billion years. Therefore there did not seem to be much need for a non-zero Λ.
After four decades of smugness, Λ has made a comeback. In 1998 some very subtle cosmological studies using distances from type Ia supernovae and linking several parameters of the universe suggested that the best fit to the data is that Λ has a small non-zero value. Since its reemergence astronomers have begun to call the cosmological constant “dark energy.” The cosmological constant corresponds to energy, because it does represent a repulsive force, and such forces always can be written as a potential energy. Einstein showed that energy and mass are equivalent, so cosmic repulsion can be viewed similarly to mass. Since neither cosmic repulsion nor dark matter can be seen, and since both critically affect the structure of the universe, it is appropriate to view the two in a similar way. As uncomfortable as this may be for some, cosmologists have been forced to reconsider the cosmological constant. Where this will lead is not known at the time of this writing.
The value of Λ has ramifications in the future of the universe. In most discussions of cosmology, the future of the universe is tied to the geometry of the universe. These discussions are based upon the model developed by the Russian mathematician Alexandre Friedman in 1922, a model that is called the Friedman universe. The Friedman universe supposes that the value of Λ is zero. In the Friedman model, if the average density of the universe is below some critical density, then the universe is spatially infinite and it will expand forever. This corresponds to negative curvature where there are an infinite number of lines through a point that are parallel to any other line. If the average density of the universe is above the critical density, then the universe is spatially finite, though it is not bound. This universe will eventually cease expanding and reverse in a contraction. The geometry of this universe has positive curvature so that there are no parallel lines. The critical density depends upon the Hubble constant. The currently accepted value of the Hubble constant results in a critical density that is higher than the density of lighted matter in the universe. Dark matter and dark energy bring the total density of the universe very close to the critical density, though no one expects it to exceed the critical density.
A universe that will expand forever is said to be open, while a universe that will cease expanding is called closed. Technically, the terms open and closed actually refer to the geometry of the universe, but with a Friedman universe they may refer to the ultimate fate of the universe as well. However, when Λ is not zero this relationship is altered. In such a universe, the open or closed status of the universe directly refers to the geometry via the density. For instance, a closed universe could expand forever. This is a fine point that many books on cosmology get wrong, because they only consider Friedman models. For many years only Friedman models were seriously considered. Since 1998 non-Friedman models have dominated cosmological thinking and with time this fine point will probably work its way into many books about cosmology.
The Origin of the Universe
The origin of the universe is a mysterious topic. For instance, the sudden appearance of matter and energy would seem to violate the conservation of energy (the first law of thermodynamics) and matter. Science is based upon what we can observe. Regardless of how or when the universe came into being, it was an event that happened only once in time (as we know time). No human being was present at the beginning of the universe, so one would expect that the origin of the universe is not a scientific question at all, but that has not kept scientists from asking whence came the big bang. As discussed further in the next chapter, some Christian apologists see in the big bang evidence of God’s existence. Their reasoning is that something cannot come from nothing, and so there must be a Creator. Cosmologists are well aware of this dilemma, and they have offered several theoretical scenarios whereby the universe could have come into existence without an external agent.
One proposal originally offered by Edward Tryon in 1973 is that the universe came about through what is called a quantum fluctuation. As discussed in the beginning of chapter 1, quantum mechanics tells us that particles have a wave nature, and thus there is a fundamental uncertainty that is significant in the microscopic world. By its very nature a wave is spread out so that one cannot definitely assign a location to the wave. Usually this principle is called the Heisenberg uncertainty principle, named for the German physicist who first deduced it. The uncertainty principle can be stated a couple of different ways. One statement involves the uncertainty in a particle’s position and the uncertainty of a particle’s momentum. Momentum is the product of a particle’s mass and velocity. Whenever we measure anything, there is uncertainty in the measurement. The Heisenberg uncertainty principle states that the product of the uncertainty in a particle’s position and the uncertainty in a particle’s momentum must be no less than a certain fundamental constant. In mathematical form this formulation of the uncertainty principle appears as
Δx Δp ħ/2
where Δx is the uncertainty in the position of a particle and Δp is the uncertainty in the momentum of a particle. The fundamental constant is ħ, called h-bar, and is equal to 1.055 x 10-34 joule-second.
What the uncertainty principle means is that the more accurately that we know one quantity (the lower that its uncertainty is), the less accurately we know the other quantity (the greater that its uncertainty is). If we measure the position of a small particle such as an electron very precisely, then we know very little about the particle’s momentum. Since we know the mass of an electron pretty well, the uncertainty in the momentum is mostly due to our ignorance of the electron’s speed. If on the other hand we know the particle’s speed to a high degree of accuracy, we will not know the particle’s position very well. Recall from the discussion in chapter 1 that this is a fundamental uncertainty, and not merely a limitation imposed by our measuring techniques. That is, even if we had infinite precision in our measuring techniques, we would still have the limitation of the uncertainty principle.
This behavior seems rather bizarre, because it is not encountered in everyday experience. The reason is that the wavelengths of large objects are so small that we cannot see the wave nature of macroscopic objects. Another way of looking at it is that ħ is very small, so small that the uncertainties in position and momentum of macroscopic systems is completely dwarfed by macroscopic errors in measurement totally unrelated to the uncertainty principle. Therefore while the uncertainty principle applies to all systems, its effects are noticeable only in very small systems where the value of ħ is comparable to the properties of the objects involved. As bizarre as the uncertainty principle may seem, it has been confirmed in a number of experiments.
Another statement of the uncertainty principle involves the uncertainty in measuring a particle’s energy and the uncertainty in the time required to conduct the experiment. In mathematical form this statement is
ΔE Δt ħ/2
where ΔE is the uncertainty in the energy and Δt is the uncertainty in the time. Basically this statement means that we can measure the energy of a microscopic system with some precision or we can measure the time of the measurement with some precision, but we cannot measure both with great precision simultaneously.
One application of this statement of the uncertainty principle is a process whereby a pair of virtual particles can be produced. The conservation of mass and energy (they are related through Einstein’s famous equation E = mc2) seems to prevent the spontaneous appearance of particles out of nothing. However, there is nothing else that prevents this from happening, and the uncertainty principle offers a way to get around this objection, if for only a short period of time. For instance, in empty space an electron and its anti-particle, the positron, can spontaneously form. This would introduce a violation of the conservation of energy, ΔE. Being anti-particles, the electron and positron have opposite charges so that they attract one another. As the two particles come into contact they are annihilated and release the same amount of energy that was required to create them. The energy conservation violation that occurred when the particle pair formed is exactly cancelled by the energy released when the particles annihilate. That is, there is no net change in the energy of the universe. As long as the particle pair exists for a short enough period of time, Δt, so that the product of ΔE and Δt does not violate the uncertainty principle, then this brief trifling violation of the conservation of energy/mass can occur. Such matters are called quantum fluctuations. A number of quantum mechanical effects have been interpreted as manifestations of quantum fluctuations.
Larger violations of the conservation of energy cannot exist for as long a time interval as smaller violations. For example, since protons have nearly 2,000 times as much mass (and hence energy) as electrons, proton/anti-proton pairs produced this way can last for no more than 1/2,000 as long as pairs of electrons and positrons created by pair production. A macroscopic violation of the conservation of energy would last for such a short length of time that it cannot be observed. However, what would happen if a macroscopic phenomenon had exactly zero energy? To be more specific, suppose that the universe has total energy equal to zero? Then the universe could have come into existence and lasted for a very long period of time, because if ΔE is zero, Δt can have any finite value and still satisfy the uncertainty principle. Therefore the universe could have come into existence without violating the conservation of energy. If this were true, then the universe is no more than a quantum fluctuation.
The trick is to find some way to make the sum total of energy in the universe equal to zero. The universe obviously contains much energy in the form of matter (E = mc2) and radiant energy (photons of all wavelengths), as well as more exotic particles such as neutrinos. There are forms of negative energy that many cosmologists think may balance all of this positive energy. The most obvious choice for this negative energy is gravitational potential energy. The gravitational potential energy for a particle near a large mass has the form
E = –GmM/r
where G is the universal gravitational constant, m is the mass of the particle, M is the mass of the large mass, and r is the distance of the particle from the large mass. This equation could be summed over all of the mass of the universe to obtain the total gravitational potential energy of the universe. Since the gravitational potential energy has a negative sign, all terms would be negative, and the sum must be negative as well. Therefore it is reasoned that the gravitational potential energy could exactly equal the total positive energy so that the total energy of the universe is zero.
However there are at least a couple of problems with this. First, we do not know the variables involved well enough to properly evaluate the energies to determine if indeed the energy of the universe is zero. Therefore it is more a matter of faith that the sum of the energy of the universe is zero. A second, more difficult, problem is with the negative sign in the gravitational potential energy equation. The sign appears because the reference point is taken at infinity. All potential energies require the selection of an arbitrary reference point where the potential energy is zero. The reference point for gravity is taken at infinity for mathematical simplicity. This forces all gravitational potential energies at finite distances to be negative. Any other zero point could be chosen, though that would make the mathematics more complicated. Any other reference point would make at least some of the gravitational potential energies positive. Alternately, one could add an arbitrary constant to the potential energy term, because the zero point is arbitrary. This is true for all potential energies. In other words, one cannot honestly state that the gravitational potential energy of the universe has any particular value to balance other forms of energy.
In his original 1973 paper on the quantum fluctuation theory for the origin of the big bang, Edward Tryon stated, “I offer the modest proposal that our universe is simply one of those things which happen from time to time.” Alan Guth has echoed this sentiment with the observation that the whole universe may be “a free lunch.” Indeed, Guth’s inflationary model depends upon a quantum fluctuation as the origin of the big bang. In the inflationary model the universe sprang from a quantum fluctuation that was a “false vacuum,” an entity predicted by some particle physicists, but never observed. While a true vacuum is ostensibly empty, it can give rise to ghostly particles through pair production. On the other hand, a false vacuum can do this and more. A false vacuum would have a strong repulsive gravitational field that would explosively expand the early universe. Another peculiarity of a false vacuum is that it would maintain a constant energy density as it expands, creating vast amounts of energy more or less out of nothing.
The quantum fluctuation theory of the origin of the universe has been expanded upon to allow for many other universes. In this view the universe did not arise as a quantum fluctuation ex nihilo, but instead arose as a quantum fluctuation in some other universe. A small quantum fluctuation in that universe immediately divorced itself from that universe to become ours. Presumably that universe also arose from a quantum fluctuation in a previous universe. Perhaps our universe is frequently giving birth to new universes in a similar fashion. This long chain of an infinite number of universes is a sort of return to the eternal universe, though any particular universe such as ours may have a finite lifetime. This idea is the multi-verse mentioned earlier that has been invoked to explain the anthropic principle. In each universe one would expect that the physical constants would be different. Only in a universe where the constants are conducive for life would cognizant beings exist to take note of such things. Thus, selection of universes in which we could exist might be limited.
Some cosmologists have suggested an oscillating universe to explain the origin of the universe. In this view, the mass density of the universe is sufficient to slow and then reverse the expansion of the universe. This would lead to the “big crunch” mentioned earlier. After the big crunch, the universe would “bounce” and be reborn as another big bang. This big bang would be followed by another big crunch, which would repeat in an infinite cycle. Therefore, our finite-age universe would merely be a single episode of an eternal oscillating universe. Some have fantasized that the laws of physics may be juggled between each rebirth.
There are several things wrong with the oscillating universe. First, the best evidence today suggests that Ω is too small to halt the expansion of the universe. Second, even if the universe were destined to someday contract, there is no known mechanism that would cause it to bounce. We would expect that once the universe imploded upon itself, it would remain as some sort of black-hole sort of state (incidentally, if the big bang started in this sort of state, then this would be a problem for the single big-bang model as well). Third, there is no way that we can test this, so it is hardly a scientific concept.
One last attempt to explain the beginning (or non-beginning) of the universe should be mentioned. If the universe is infinite in size, then it has always been and always will be infinite in size. As the universe expands, it becomes larger and cooler, and its density decreases. What if the universe has been expanding forever? One possibility is that the physical laws that govern the universe change as the average temperature changes. This is the essence of GUT described earlier. Most physicists think that the fundamental forces that we observe today are different manifestations of a single force that has had its symmetry broken. Perhaps in much earlier times when the universe was much hotter and denser, other laws of physics totally unknowable to us were in effect. If this were true, then what we call the big bang was just a transition from a much higher density and temperature state. The big bang would have been some sort of wall beyond which we cannot penetrate to earlier times with our physics. Before the big bang the universe would have contained unbelievable densities and temperatures, and the physical laws would have been quite foreign to us. Thus the universe has always been expanding through various transitions, and there is no ultimate beginning to explain. This, too, represents a return to the eternal universe that the big bang was long thought to have eliminated.
Big-bang research of recent years has been in the direction of explaining the origin of the universe in an entirely physical, natural way without recourse to a Creator. Any purely physical explanation of origins without a Creator amounts to non-theistic evolution, naturalism, and secular humanism. All these ideas are antithetical to biblical Christianity. Those Christian apologists who fail to see this simply have failed to understand the direction that cosmology has taken in recent years.
Checking Your Understanding
- What is the flatness problem?
- What is the anthropic principle?
- What is inflation?
- What is dark matter?
- What did the COBE and WMAP missions find?
- What is dark energy?
- What is the Hubble time?
- What are some ways that cosmologists have suggested that the universe began?
Universe by Design
This book explores the universe, explaining its origins and discussing the historical development of cosmology from a creationist viewpoint.
Read Online Buy BookFootnotes
- The definitive work on the anthropic principle is the one by Barrow and Tipler, The Cosmological Anthropic Principle (Oxford, England: Oxford University Press, 1988). Interestingly, Barrow and Tipler fully discuss the evidence for the anthropic principle before finally concluding that the universe merely appears designed.
- See for instance, H. Ross, The Fingerprint of God (Orange, CA: Promise Publishing, 1989); or H. Ross, The Creator and the Cosmos (Colorado Springs, CO: Navpress, 1995). For a critical analysis of Hugh Ross’s apologetics, see D.R. Faulkner, “The Dubious Apologetics of Hugh Ross,” Creation Ex Nihilo Technical Journal 13(2): 52–60 (1999).
- See, for instance, M. Rees, Before the Beginning: Our Universe and Others (Reading, MA: Helix Books: 1997).
- H. Ross, Beyond the Cosmos (Colorado Springs, CO: Navpress, 1996). For reviews of this book, see W.L. Craig, Journal of the Evangelical Theological Society 24(2): 293–304 (1999), or D.R. Faulkner, Creation Research Society Quarterly 34:242–243 (1998).
Recommended Resources

Answers in Genesis is an apologetics ministry, dedicated to helping Christians defend their faith and proclaim the good news of Jesus Christ.
- Customer Service 800.778.3390
- Available Monday–Friday | 9 AM–5 PM ET
- © 2026 Answers in Genesis



