
Chapter 1
Twentieth-Century Cosmology
Modern Physics
For two centuries Newtonian physics had successes unparalleled in the history of science, but toward the end of the 19th century several experiments produced results that had not been anticipated. These results defied explanation with Newtonian physics, and this failure led in the early 20th century to what is called modern physics. Modern physics has two important pillars: quantum mechanics and general relativity. Quantum mechanics is the physics of small systems, such as atoms and subatomic particles. General relativity is the physics of very high speeds or of large concentrations of mass or energy. Both of these realms are beyond the scope of everyday experience, and so quantum mechanical and relativistic effects are not usually noticed. In other words, Newtonian mechanics, which is the physics of everyday experience, is a special case of modern physics.
Some creation scientists view both quantum mechanics and general relativity with suspicion. Part of the suspicion of quantum mechanics stems from the Copenhagen interpretation, a philosophical view of quantum mechanics. In quantum mechanics, the solution that describes location, velocity, and other properties of a particle is a wave function. The wave function amounts to a probability function. Where the value of the wave function is high, there is a high probability of finding the particle, and where the value of the wave function is low, there is a small probability of finding the particle. This result is pretty easy to understand when one considers a large number of particles—where the probability is high there is a greater likelihood of finding more particles.
However, how is one to interpret the result when considering only a single particle? The Copenhagen interpretation states that the particle exists in all possible states simultaneously. The particle exists in this weird state as long as no one observes the particle. Upon observation we say that the wave function collapses and the particle assumes some particular state. If the experiment is conducted often enough, the distribution of outcomes of the experiment matches the predictions of the probability function derived from the wave solution.
This suggests a fundamental uncertainty about the universe that runs counter to the Christian view of the world and an omniscient God. An omniscient God would presumably know the outcome of any experiment, an idea that is supported by the pre-determined world of Newtonian mechanics. With Newtonian mechanics if one knows all the properties, such as location and velocities of particles at one time, all such properties of the particles can be uniquely determined at any other time. This ability is called determinism. It would appear that quantum mechanics leads to a fundamental uncertainty that even God cannot probe. Uncertainty usually results from ignorance, that is, we lack enough input information to be able to calculate future states of a system. However, the uncertainty introduced by quantum mechanics is not one of ignorance, and so we call this uncertainty fundamental. By “fundamental uncertainty” we mean that even if we had infinite precision of all the relevant variables, we would still fail to predict the outcome of future experiments. Possible responses to this objection are that either the Copenhagen interpretation is wrong or that quantum mechanics is an incomplete theory. Phillip Dennis1 has argued that quantum mechanics is probably an incomplete theory and that the uncertainty is no problem for the Christian.
One objection to modern relativity theory comes from the misappropriation of the term by moral relativists. Moral relativists claim that everything is relative and that general relativity has given physical evidence of this. General relativity says no such thing. In fact, it says just the opposite, that there are certain absolutes. Even if this assertion were true, this is a specious argument. Physical laws have no bearing upon morality and ethics. Another reservation about relativity that some creationists have is its perceived intimate relationship with the big-bang cosmogony. The reasoning seems to be that if the big bang is not true, then relativity is not true either. But the big bang is just one possible result from relativity. Creation-based cosmogonies could be generated with relativity theory, as has been attempted by Russ Humphreys.2
Those who doubt either or both pillars of modern physics also express discomfort with them, feeling that they just defy “common sense.” However, there are many things about the world that defy common sense. For instance, the author of this book never ceases to be amazed by Newton’s third law of motion, that when an object exerts a force upon another object, the second object exerts an opposite and equal force upon the first object. We shall see shortly that one of the questions addressed by general relativity is how gravitational force is transmitted through empty space. Newtonian physics simply hypothesizes that the force instantly and mysteriously acts over great distances. This too defies common sense. The important question for any theory is how well it describes reality.
Both theories of modern physics have been extensively tested in experiments and have proven to be very robust theories. These theories have been better established than almost any others in the history of science. Therefore in what follows it will be assumed that these models are correct, if not complete. Both theories play important roles in modern cosmology, but only relativity is significant in the historical development of modern cosmology, so further discussion of quantum mechanics will be deferred until the next chapter.
While many people worked on the foundation of modern relativity theory, Albert Einstein usually receives most credit. His special theory of relativity was published in 1905, followed by his general theory in 1916. The special theory is not that difficult to understand. It deals with the situations of constant speeds near the speed of light. Suppose that a space ship were moving at 60% the speed of light toward a stationary person. Now suppose that the stationary person shined a light toward the moving astronaut. One might think that if the moving observer measured the speed of the light beam, that speed would be 160% the speed of light. If, on the other hand, the space ship were moving away, one might expect that the measured speed of the light would be 40% of the normal speed of light. However, actual measurement reveals that the speed of light is a constant no matter how much the observer may be moving. This sort of result was obtained by the famous Michelson-Morley experiment in 1887. This fact was one of the first experiments that showed the failure of classical Newtonian mechanics.
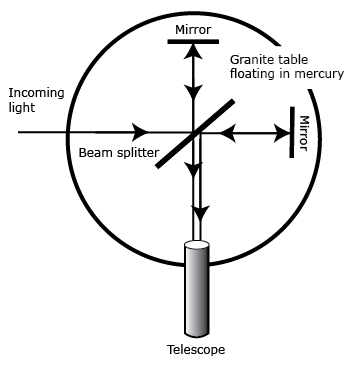
Image courtesy of Bryan Miller
Michelson-Morley Experiment
Einstein took the invariance of the speed of light as a postulate and examined the consequences. He found that near the speed of light, time must slow down as compared to time measured by someone who is not moving. The length of the spacecraft must decrease as speed increases, and the mass of the body must increase with increasing speed. These effects are respectively called time dilation, length contraction, and mass increase, and all have been confirmed in numerous experiments. Incidentally, special relativity predicts that mass increases toward infinity as speed approaches the speed of light. Thus, to achieve light speed would require an infinite amount of energy. This is impossible, so no particle that has mass can move as fast as the speed of light.
General relativity is concerned with accelerated motion at high speeds. Unfortunately it requires the use of complicated mathematical abstractions, and so it is not easy to understand. While we will not discuss any mathematical detail, we will qualitatively describe what the theory attempts to do.
As stated earlier, one question that general relativity attempts to explain is how gravitational force is transmitted through empty space. The sun is 93 million miles from the earth, and yet the earth somehow not only knows how far away the sun is, but also in which direction the sun is and how much mass the sun has. All of this information is necessary to determine the force of gravity. In Newtonian theory, gravitational force acts at a distance with no guess as to how the information necessary or the force is transmitted over the distance. General relativity answers this question by treating space as a real entity through which information can be transmitted like a wave. Space and time are handled in a similar fashion so that space can be thought of as consisting of four dimensions, three of space and one of time. The equations of general relativity tell how to treat the four dimensions of space. Any two dimensions of space could be represented as lines on graph paper, but instead of being flat like graph paper, the space is curved. The mathematics of curved space is similar to that of a curved sheet of graph paper.
What causes curvature of space? On a large scale it can be a property of space itself, but on the local level curvature results from the presence of matter or energy. It takes a large amount of energy or matter to curve space. Greater mass or energy will curve space by a greater amount. The mathematical expressions of general relativity describe the amount of curvature present as a result of the mass or energy. Keep in mind that space here refers to a four-dimensional manifold that includes time, so we should properly call it space-time. Objects move through space on straight paths called geodesics. If the space-time through which an object moves is flat, then that object will appear to us to move in a straight line or remain at rest. If on the other hand there is much matter or energy present so that the space-time is curved, the straight trajectory of the object through space-time will cause the object to appear to accelerate as we observe it.
While gravity is still a mysterious force, general relativity has removed some of the mystery and offered a more fundamental explanation than Newtonian theory. Newton posited that gravity reached great distances through empty space without any explanation, but general relativity offers a mechanism of how action at a distance works. The earth is following a geodesic in space-time. If the sun were not there, the space-time would not be curved and the earth would appear to us to move in a straight line. That is, the earth would not be accelerated. However, the large mass of the sun produces bending in space-time that is transmitted outward. At the location of the earth, the earth moves along a geodesic in the curved space-time. The earth’s straight-line motion through curved space-time appears to us as acceleration.
Newtonian physics and general relativity treat space and time very differently. In Newtonian physics, space is not much more than a backdrop upon which masses move in time. Thus space, matter, and time are very distinct things. In general relativity, space and time are treated very similarly, and both have an intimate relationship with matter and energy. In Newtonian physics the presence of matter and energy have no effect upon space and time, while in general relativity they do. This is more than just a philosophical difference; it results in some definite differences in predictions that can be tested, as we shall now discuss.
At the time Einstein introduced his theory, people realized that an upcoming total solar eclipse offered an excellent opportunity to test general relativity. The theory predicts that as light passes near a large mass, the light rays should be slightly deflected toward the large mass due to the mass’s gravity. Therefore if general relativity were true, stars observed near the edge of the sun during a total solar eclipse should appear a little closer to the sun than they would if general relativity were not true (see illustration on opposite page). During the 1919 total solar eclipse, a photograph was taken of the eclipsed sun and a number of stars near the edge of the sun. The positions of the stars were carefully measured and compared to their positions on a photograph made six months earlier. The shifts in the positions of the stars were consistent with the predictions of general relativity, and so this was hailed as the first confirmation of the theory.
There is a very small, but vocal minority of physicists who reject general relativity. They argue against this experiment on the basis that the errors in the measurements are very large and could have swamped the effect being measured. There is some legitimacy to this claim. The relativistic effect is very small and the errors of measurement and the corrections due to refraction of the earth’s atmosphere were rather large. If this were the end of the matter, then the anti-relativists would have a basis of complaint here. But that was not the end of the matter. Similar experiments have been conducted during numerous eclipses since 1919, each with improving accuracy and agreement with the predictions of general relativity.
Furthermore, since the early 1970s, very long base interferometry (VLBI) has enabled us to repeat the experiment with much greater precision. VLBI combines simultaneous observations from widely separated radio telescopes to measure positions of radio sources with unprecedented accuracy. Distant point-radio sources that lie on the ecliptic (the plane of the earth’s orbit around the sun) have had their positions in the sky measured with VLBI. Lying in the earth’s orbital plane, the sun passes in front of these objects once each year. We can remeasure the positions of the point-radio sources when this happens. The differences in the measurements of the positions give us the amounts of shifts caused by the radio waves passing near the edge of the sun. The accuracy of the measured shifts in positions is orders of magnitude better than the accuracy of the 1919 eclipse shifts. This experiment has been repeated a number of times, and in every case the observed shifts match the predictions of general relativity very well.
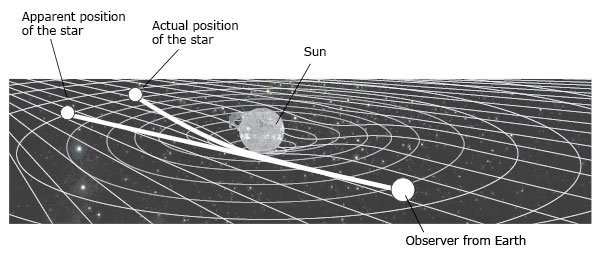
Image courtesy of Bryan Miller
When Einstein applied his field equations to the universe, his solution showed that his theory had difficulty explaining the universe as then understood. In the previous chapter we saw that Newton believed that the universe was eternal, but that his theory of gravity would cause the universe to have long ago collapsed upon itself. To avoid this difficulty Newton hypothesized that the universe was infinite in size. He reasoned that only then would all matter be attracted equally in all directions to produce a static universe. A static universe is one in which the matter is neither contracting nor expanding. But in Einstein’s alternative theory of gravity even the appeal to an infinite universe failed. With general relativity, an infinite universe will eventually collapse upon itself, resulting in infinite density everywhere. This is obviously not the case, so Einstein had to solve this problem.
The answer that Einstein chose was to introduce what is called the cosmological constant into his solution. The cosmological constant, indicated by the Greek letter lambda (Λ), acts as a sort of anti-gravity. It amounts to a self-repulsion term that space has, but is locally very weak. However, over great distances this feeble space repulsion would accumulate to become an important factor in the structure of the universe. By finely tuning Λ to cancel the effect of gravity, Einstein was able to produce a static universe, as most people for some time thought that the universe must be. If Λ is not fine-tuned to counterbalance gravity, then the universe must either expand or contract.
The introduction of Λ was soon criticized, and Einstein later admitted that it was the biggest blunder that he ever made. However Einstein was much too harsh upon himself on this point. His field equations are differential equations, a type of calculus-based mathematics frequently encountered in the physical world. The general solution of a differential equation does contain a constant. Differential equations are frequently employed in physics, and the constants involved are usually set by the initial conditions of the problem. Often these constants turn out to be zero. The initial conditions of the universe determine what Λ is, but we do not know those initial conditions. Observations of the universe could tell us the value of Λ, but this is not an easy task. For decades most data have suggested that Λ is zero, but suggestions that it is nonzero continue to arise. If Λ is not fine-tuned to counterbalance gravity, then the universe must either expand or contract.
The Early Big-Bang Model
Within two years of the publication of Einstein’s theory of general relativity, a Belgian priest named Abbe LeMaitre had used it to produce the first model that presaged the currently accepted cosmological model, the big bang. Le-Maitre called his model the “cosmic egg,” which was rather simplistic by modern standards. He envisioned that the universe began with all of its matter and energy concentrated into a very hot sphere that expanded and cooled into the universe that we see today. One could ask how LeMaitre knew that the universe was expanding, rather than contracting or being static. One possibility is that he merely guessed, with some intuition from a definite and theistic origin of the universe in the finite past. That would have eliminated the static universe. It may have made more sense to him that the universe began small and expanded rather than starting large and then contracting, thus eliminating the contracting universe.
Another possibility is that Le-Maitre may have known of the work of Vesto Slipher, a Lowell Observatory astronomer, just a few years earlier. In 1913 Slipher showed that many of the “nebulae” had large redshifts, indicative of speeds many hundreds or even thousands of kilometers per second away from us. This was a decade before the confirmation of the island universe theory, so these “nebulae” were not yet recognized as external galaxies. As members of our galaxy, the large redshifts of these “nebulae” made no sense, but if they were external galaxies, the redshifts made perfect sense in light of the predictions of Einstein’s model: the universe is expanding.
After his confirmation of the island universe idea in 1924, Hubble certainly understood the significance of the redshifts of other galaxies. If this was evidence of the expansion of the universe, then there must also be a relationship between the amount of redshift and distance. Why are redshift and distance related? Anyone who has participated in or watched a 10-km race can see this. Within ten minutes of the start of the race, runners will be stretched out over considerable distance. The swiftest runners will be most distant from the starting line, while the slowest runners will be closest to the starting line. Runners of all intermediate speeds will be scattered between those extremes. As a result there will be a direct relationship between speed and distance from the starting line.
A similar thing will be true of galaxies. Those galaxies most distant now will be those that are made of material that was traveling away most swiftly at the beginning of the universe, while those that are closest now are made of material that was originally moving very slowly. It should be emphasized that this simple analogy, while useful for illustration, has several flaws. One is that the race involves only one spatial dimension while the expansion of the universe involves three. Another is that the analogy implies that the universe has a center and that the earth is near it. Most cosmological models today do not have a center. Lastly, the analogy implies that the measured redshifts are Doppler shifts due to motion through space. This is not true; Doppler shifts and redshifts are two very different things. This distinction and the lack of a center for the universe will be discussed in chapter 3.
In 1928 Hubble presented the relationship between the distance and redshift. This dependence has become known as the Hubble relation, and can be expressed as Z = H0D, where Z is the redshift, D is the distance, and H0 is the constant of proportionality called the Hubble constant. Distances are usually expressed in mega parsecs (Mpc). An Mpc is a million parsecs, and a parsec is 3.26 light years, so an Mpc is 3.26 million light years. A light year is the distance that light travels in a year. Z can be expressed in km/sec, so the units of H0 are km/sec Mpc. H0 measures the expansion rate of the universe, and its value is the slope of the line representing the plot of redshift versus distance for a large number of galaxies. Measuring redshift by means of spectroscopy is straightforward and unambiguous, but finding distance is a difficult task and subject to many assumptions and potential errors. The appendix has a brief discussion of some of the methods of finding astronomical distances. Hubble initially found H0 to be over 500 km/sec Mpc, but by the 1960s H0 had been decreased to a little more than 50 km/sec Mpc. In the 1990s several studies suggested that H0 be increased to about 80 km/sec Mpc. This is of more than academic interest, because it affects the age of the big-bang universe, which will be discussed later.
The Cosmological Principle
Before the equations of general relativity are applied to the universe, a couple of assumptions are usually made. One assumption is that the universe is homogeneous. Homogeneity means that the universe has the same properties throughout. Of course homogeneity must include the universality of physical laws, or else science would not even be possible. In cosmology, homogeneity usually refers to the appearance and structure of the universe as well as the matter distribution. If the matter in the universe is clumpy, then the equations of general relativity cannot be applied easily, so this assumption is primarily based upon our ability to do the math. On a local level the universe appears very clumpy. For instance, in stars and planets the matter density is high, but in the vast expanses of space between stars and planets matter is almost non-existent.
This is a common problem in physics—we frequently encounter situations where the mass involved is clumpy. Consider a gas. We know that it is made of many tiny particles called atoms that are separated by distances that are large compared to the sizes of the atoms. However, from a macroscopic approach we can treat the gas as if it is made of some continuous fluid. At a macroscopic level the gas appears homogeneous and its clumpy microscopic nature can be ignored. Similarly, it is assumed that at some grand scale the universe is homogeneous, but at the largest scale so far probed (clusters of clusters of galaxies) the universe still appears clumpy. If the universe is in fact inhomogeneous, it is not known what effect that will have on our cosmology.
Another common assumption is that the universe is isotropic. Isotropy means that the universe has the same appearance or properties in all directions. This insures that the expansion is the same in all directions. If there were a net flow in one direction, then the universe would not be isotropic. There are other ways that the universe might not be isotropic. A few years ago some astronomers found that distant radio sources had their polarizations altered by amounts that depended upon distance but also upon direction in the sky. Polarization is a term used to describe the direction that waves are vibrating. A wave can vibrate in any direction perpendicular to the direction that the wave is traveling. Usually, electromagnetic waves vibrate in many directions, but frequently the waves oscillate predominantly in one direction. When this happens, we say that the wave is polarized. The observation that distant radio sources were polarized depending on their directions in space suggested that the universe is fundamentally different in different directions, that is, it is not isotropic.
The assumption of homogeneity and isotropy together is called the cosmological principle. The cosmological principle along with the observation of the expansion of the universe usually leads to the big-bang model. However the big-bang model is not the only possible model in an expanding universe governed by general relativity. The big-bang model forces one to accept that the universe had a beginning. However, this possibility is unpalatable to many, as discussed previously, and also as witnessed by Einstein’s fudging of the value of Λ to get a static, eternal universe.
Another attempt to produce an eternal universe starts with the assumption of the perfect cosmological principle. The perfect cosmological principle states that the universe has been homogeneous and isotropic at all times. The phrase “at all times” means that the universe always has and always will be as it is today. In this view, stars and galaxies are continually being born, growing old, and dying, but the universe remains the same forever. Since in this model the universe never changes, this is called the steady-state theory. You may ask, “if the universe is expanding, its average density should be decreasing, so how could the universe remain unchanged as per the steady-state theory?” In order for the steady-state universe to maintain a constant density, matter must spontaneously come into existence. Another name for the steady-state theory is the continuous creation theory. Some may object that this violates the law of conservation of matter, but the law of conservation of matter is merely a statement of how we see the universe operate. The rate of new matter production per unit volume required to maintain a constant density in the universe is so small as to escape our notice. Those who support the steady-state theory argue that the law of conservation of matter is only an approximation of how the universe really works.
In the 20 years prior to 1965 the steady-state theory enjoyed much support. Its appeal stemmed from the avoidance of a beginning and its ultimate simplicity and beauty. It was once described as being so beautiful that it must be true. Meanwhile the details of the competing model, the big bang, were being developed. One of the strongest supporters of the steady-state model, the late Sir Fred Hoyle, is credited with naming the other model when he, in exasperation, declared, “The universe did not begin in some big bang!” To Hoyle’s chagrin, the name stuck, despite attempts to find a better name for it.
Alleged Evidences of the Big Bang
Several evidences against the steady-state theory have been presented, but the most devastating one was the 1964 (published in 1965) discovery of the 3K cosmic background radiation (CBR) by Arno Penzias and Robert Wilson. In 1978 Penzias and Wilson received the Nobel Prize in physics for their work. As researchers at the Bell labs in New Jersey, they were developing technology for microwave transmissions for communication. Penzias and Wilson had detected a background noise for which they could not find a source, and seemed to coming from all directions. In 1948 George Gamow had predicted that such a radiation should be seen throughout the universe, but the technology for detection did not exist at that time. By the 1960s the technology did exist, and Robert Dicke of Princeton University was planning the construction of equipment to observe the CBR when he happened to discuss the matter with Robert Wilson. Dicke encouraged Penzias and Wilson to publish their findings, along with a companion paper by Dicke that explained the significance of the find.
According to the big-bang model, the photons in the CBR came from a time when the universe was a few hundred thousand years old and at a temperature of about 3,000K. At that time most of the matter in the universe would have been protons and electrons, but the temperature and density were too high for hydrogen atoms to form. In this hot gas, photons would have been continually absorbed and reemitted so that the matter and energy would be in equilibrium and the radiation would have had a blackbody spectrum that was a function of the temperature at that time. As the universe expanded, the gas cooled and the density decreased to the point that stable hydrogen began to form and remained un-ionized as atoms. This time in the history of the universe is called the age of recombination, though a better name might be the age of combination, since the atoms did not previously exist.
According to the model, after the age of recombination, the matter in the universe no longer absorbed and reemitted all of the radiation, and the universe became transparent for the first time. Prior to the age of recombination, matter and energy were coupled in that the radiation could not escape the matter. Because light was so easily absorbed and reemitted, the mean free path of photons was extremely short. After the age of recombination the photon mean free path became virtually the size of the universe and energy managed to escape matter for the first time. We say that matter and energy would have become decoupled. The photons liberated during the age of recombination have traveled with little interaction in the ensuing 10–15 billion years. The photons have maintained a blackbody spectrum, but the universe has expanded a thousandfold in size since the age of recombination, so the blackbody spectrum has been redshifted by a factor of 1,000. The redshift reduced the effective temperature of the blackbody from 3,000K to 3K.
The steady-state theory does not predict the CBR, because in the steady-state theory the universe has always appeared the same as it does today, so there was never a time when the universe had a temperature of 3,000K. Some have hailed the CBR as one of the greatest discoveries of 20th century astronomy, because it eliminated the steady-state theory and “proved” the big-bang theory. Since the mid 1960s the big-bang model has reigned as the only viable model in the estimation of most cosmologists, so it has been dubbed the “standard cosmology.” This does not mean that all opponents of the standard cosmology have given up. For years Hoyle continued to modify the steady-state theory so that it too would predict the CBR, but he was not successful. Hoyle and some of his associates, such as Geoff Burbidge and Halton Arp, have pointed out numerous problems with the big-bang theory. Some of these difficulties will be discussed in chapter 4.
The standard cosmology has been a very robust and quantitative model, as indicated by the many highly technical papers on the subject published each year. When asked how astronomers know that the big bang is the correct scenario of the origin of the universe, three evidences are usually put forth. One evidence is the CBR, as just discussed. The other two are the expansion of the universe and the abundances of the light elements. But how good are these evidences? Before answering this question, we should investigate just a bit the nature of proof and prediction in science.
Proof and Prediction
A scientific theory is judged upon how well it explains data. Data may be divided into classes: the data already in hand when the theory is developed and new data from experiments inspired by the theory. The data already available are used to guide the construction of a theory. A good theory should be able to account for all, or at least most, of that data. In other words, a theory should be able to explain what we already know. If it does, then we say that the theory has good explanatory power. If a theory does not have good explanatory power, then it should be modified so that it does or should be replaced by another theory that does.
Once a theory is developed, it can be used to make certain predictions about the results of experiments. When an experiment is performed, the predictions of the theory can be compared to the data from the experiment. If the predictions match the data, then we say that the theory has been “proved,” though proof in this context is a bit different from what is meant in deductive reasoning or even in everyday use. A better choice of words would be to say that the theory is confirmed. If the theory’s predictions do not match the data, then the theory has been disproved, and the theory must be either modified or replaced. One strange aspect of science is that while we can disprove theories, being totally certain that any theory is absolutely correct is not possible. The history of science is filled with theories that once enjoyed proof or confirmation only to ultimately be disproved. Examples of these discarded theories include the phlogiston theory of combustion, the caloric theory of heat, and abiogenesis.
We can say that a theory has predictive power if its predictions have been tested by experimentation. Many theories have explanatory power but lack predictive power. This is especially true of the historical sciences. Much of the alleged proof for biological evolution is explanatory rather than predictive in nature. Evolution is purported to explain what we observe, but it is difficult to conceive of experiments that could clearly test what has happened in the past. The same is true of creation. In either case the question of falsifiability arises. If no experiment can be conducted that could possibly disprove the theory, then the theory is not falsifiable. Any number of scenarios could be concocted to explain a phenomenon, but the mere explanation of the facts in hand hardly constitutes proof. A good theory should possess both explanatory power and predictive power.
Are the three evidences for the big bang explanatory or predictive in nature? The expansion of the universe is definitely explanatory and not predictive. General relativity suggested that the universe should be expanding or contracting, but it could not predict which. The fact that the universe is expanding could only be determined observationally. Much later the big-bang model was developed to explain the datum that the universe is expanding. Any number of models could be constructed to explain the expansion. The steady-state model was one of those attempts. Neither cosmology predicted the expansion, but they merely responded to that fact as a means of explanation.
The evidence concerning the abundances of the light elements is subtler, but this too appears to be explanatory rather than predictive. The elements in question here are hydrogen, deuterium, a rare heavier isotope of hydrogen, the two isotopes of helium (He3 and He4) and lithium. Each of these elements would have been produced in the first few minutes of the big bang. All the heavier elements are presumed to have formed in stars. The big-bang cosmology does predict the abundances of the light elements, but most people fail to realize that information concerning elemental abundances was input in creating the model. Knowledge of the light element abundances was required in constraining which subset of possible models was viable. In fact, small changes in our understanding of these abundances have allowed cosmologists to fine-tune their models. It would be most strange if a model did not “predict” the parameters that were input for the theory. It would show that the model was internally inconsistent.
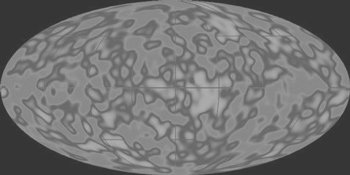
Image courtesy of NASA
Cosmic background radiation (CBR) image
The CBR does appear to be a clean prediction of the big-bang model. The CBR was first predicted nearly two decades before its discovery. Even though the discovery by Penzias and Wilson was serendipitous, there were others who were making plans to mount a search for the CBR. The big-bang model could not predict the exact temperature of the CBR, but an estimate of the range of temperature was possible. The measured temperature was near the lower end of the range. The CBR is real, and its existence has been confirmed many times. Therefore denying its existence is not an option. The extremely smooth shape of the CBR spectrum is difficult to explain any other way. The CBR elevates the status of the predictive power of the standard cosmology. It is the only prediction of the theory. Further studies of the CBR will be discussed in the next chapter.
The Geometry of the Universe
Before moving onto other topics, a few concepts about the geometry of the universe should be addressed. Space can be bound or unbound. Being bound refers to space having an edge or boundary. In two-dimensional space, a tabletop is bound, because it has a definite boundary, the edge of the tabletop. On the other hand, a mathematical plane would be unbound, because it extends indefinitely in all directions and hence has no boundary. It is difficult to conceive of our three spatial dimensions being bound. If space had a boundary, one must wonder what the nature of the boundary would be. Would it be some sort of wall that would forbid us to cross? If so, of what would the wall be made, and why could we not cross it? Would there be another side, and if so, what would it be like and could information pass through the wall? If these sorts of questions had any real answers, then it would seem that the other side of the boundary is part of our universe as well, so the wall is not really an edge after all. On the other hand, a universe without a boundary would seem to extend forever and would thus be infinite in size. As difficult a concept that a bound universe may be, a universe that has no spatial end is scarcely easier for the human mind to comprehend.
So we seem to be stuck with the choice between an infinite and unbound universe and a universe that is finite and bound. Is there a way past this dilemma? Yes. Recall that according to general relativity space may have some overall curvature. It is possible that space may curve back upon itself so that it has no boundary, but it is finite in size. Consider a two-dimensional example. A flat, two-dimensional object, such as a piece of paper, is usually finite in size and has a boundary. On the other hand, the surface of the earth is two-dimensional, but it is curved back onto itself. Therefore, the surface of the earth has no boundary or edge, but it is finite in size. If you traveled in a straight line on the earth’s surface you would eventually return to your starting point. In like fashion, if the universe is closed back on itself and if you traveled in a straight line, you would eventually return to your starting point. Such a universe would be finite in size and unbound, and thus we could avoid both an infinite universe and a bound universe.
Checking Your Understanding
- What are the two pillars of modern physics?
- What is the main difference between the Newtonian physics and the modern physics views of gravity?
- What was the first confirmation of Einstein’s theory of general relativity?
- What is a static universe?
- What is the cosmological constant?
- What does homogeneity mean?
- What does isotropy mean?
- What is the cosmological principle? What model usually stems from the assumption of the cosmological principle?
- What is the perfect cosmological principle? What model usually follows from the assumption of the perfect cosmological principle?
- What is the significance of the cosmic background radiation?
- Why are the expansion of the universe and the abundances of the light elements not proper evidence for the big-bang theory?
- What does it mean for the universe to be bound?
Universe by Design
This book explores the universe, explaining its origins and discussing the historical development of cosmology from a creationist viewpoint.
Read Online Buy BookFootnotes
- R.E. Walsh, editor, The Fourth International Conference on Creationism, by P.W. Dennis (Pittsburgh, PA: Creation Science Fellowship, 1998), p. 167–200.
- D.R. Humphreys, Creation and Time (Green Forest, AR: Master Books, 1994).
Recommended Resources

Answers in Genesis is an apologetics ministry, dedicated to helping Christians defend their faith and proclaim the good news of Jesus Christ.
- Customer Service 800.778.3390
- Available Monday–Friday | 9 AM–5 PM ET
- © 2025 Answers in Genesis


